机器学习算法的核心在于利用数据构建模型以解决实际问题，而理解其理论基础是高效应用的关键。本文从机器学习的基本概念出发，详细解析监督学习中的几种经典算法，如逻辑回归、决策树和支持向量机（SVM）。同时，我们将结合Python代码，展示这些算法如何在实际任务中应用。

1. 机器学习的基本概念

机器学习是人工智能的一个重要分支，它旨在让计算机通过数据自动学习模式，而无需明确编程规则。以下是关于机器学习的一些核心概念和分类。

---

1.1 什么是机器学习？

**机器学习（Machine Learning, ML）**是一种通过算法分析数据并从中学习规律，最终对未知数据进行预测或决策的技术。它的本质是通过数据构建模型，让机器具备“学习”的能力。

• 输入： 原始数据和目标（如特征和标签）。
• 输出： 能够对未知数据进行预测或分类的模型。
• 关键步骤：
  1. 数据准备：获取和清洗数据。
  2. 模型训练：利用算法在数据上训练模型。
  3. 模型评估：检查模型性能并优化。

例子：

• 给机器一组标注了“垃圾短信”和“正常短信”的数据，让它学会如何区分新短信是否为垃圾。
• 输入：短信文本和对应的标签（垃圾或正常）。
• 输出：一个能准确预测垃圾短信的模型。

---

1.2 机器学习的主要分类

机器学习根据学习方式的不同，可分为以下三大类：

1.2.1 监督学习（Supervised Learning）

• 定义： 使用标注好的数据训练模型，目标是学习输入特征与输出标签之间的关系。
• 目标： 构建一个能够预测新数据标签的模型。
• 常见任务：
  • 分类（Classification）： 将输入数据分为有限的类别。
    • 示例：垃圾短信分类（垃圾或正常）。
  • 回归（Regression）： 预测连续值。
    • 示例：房价预测。
• 算法：
  • 逻辑回归（Logistic Regression）。
  • 支持向量机（SVM）。
  • 决策树（Decision Tree）。

1.2.2 无监督学习（Unsupervised Learning）

• 定义： 使用没有标签的数据训练模型，目标是从数据中发现模式或结构。
• 目标： 挖掘数据的潜在结构。
• 常见任务：
  • 聚类（Clustering）： 根据数据特征自动分组。
    • 示例：将客户分组以制定个性化营销策略。
  • 降维（Dimensionality Reduction）： 简化数据特征维度，保留主要信息。
    • 示例：PCA（主成分分析）。
• 算法：
  • K-means。
  • 层次聚类。
  • 主成分分析（PCA）。

1.2.3 强化学习（Reinforcement Learning）

• 定义： 通过奖励和惩罚机制让智能体学习如何与环境交互，以实现长期收益最大化。
• 目标： 寻找最优策略。
• 常见任务：
  • 游戏AI（如AlphaGo）。
  • 自动驾驶。
• 特点：
  • 不直接依赖标注数据。
  • 重点在于智能体与环境的动态交互。
• 算法：
  • Q-learning。
  • 深度强化学习（Deep Q-Network, DQN）。

---

1.3 机器学习模型的基本组成

任何机器学习模型都可以分为以下几部分：

1.3.1 数据

数据是机器学习的基石，模型的好坏很大程度上依赖于数据质量和数量。

• 特征（Features）： 输入数据中的关键属性，例如短信的长度或出现的关键词。
• 标签（Labels）： 输出目标，例如“垃圾”或“正常”。

1.3.2 算法

算法决定了如何从数据中学习规律。

• 常用算法：逻辑回归、决策树、支持向量机等。
• 算法选择依据：数据特性（线性或非线性）、任务类型（分类或回归）。

1.3.3 损失函数

损失函数衡量模型的预测结果与真实值之间的差距。

• 目标：通过优化算法最小化损失函数。
• 示例：
  • 回归问题使用均方误差（MSE）。
  • 分类问题使用交叉熵损失。

1.3.4 模型评估

通过性能指标评估模型效果，例如：

• 准确率（Accuracy）：正确分类的比例。
• 精确率（Precision）：预测为正的样本中真正为正的比例。
• 召回率（Recall）：正样本中被正确预测为正的比例。

---

1.4 机器学习的应用领域

机器学习已广泛应用于各个领域：

• 自然语言处理（NLP）： 垃圾邮件分类、情感分析。
• 计算机视觉： 图像分类、物体检测。
• 推荐系统： 电商商品推荐、个性化内容推送。
• 金融领域： 贷款风险预测、股票价格预测。
• 医疗健康： 疾病诊断、药物研发。

2. 常见机器学习算法理论

2.1 逻辑回归

• 原理： 基于线性回归，但输出值通过Sigmoid函数映射到[0,1]之间，适合二分类任务。
• 应用场景：
  • 垃圾短信分类。
  • 疾病诊断（是否患病）。
• 核心公式：
  • Sigmoid函数：
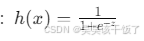
  • 损失函数：交叉熵损失。

代码实现：

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据
data = load_iris()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 模型训练
model = LogisticRegression()
model.fit(X_train, y_train)

# 预测与评估
y_pred = model.predict(X_test)
print("逻辑回归准确率:", accuracy_score(y_test, y_pred))

2.2 决策树

• 原理： 通过树状结构将数据集划分成不同的子集，以实现预测或分类。
• 重要概念：
  • 信息增益：衡量划分节点的质量。
  • 过拟合：过度拟合训练数据，需要剪枝。
• 优缺点：
  • 优点：易解释，适合处理非线性数据。
  • 缺点：易过拟合。

代码实现：

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris

# 加载数据
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 决策树模型
tree_model = DecisionTreeClassifier(max_depth=3)
tree_model.fit(X_train, y_train)

# 预测与评估
y_pred = tree_model.predict(X_test)
print("决策树准确率:", accuracy_score(y_test, y_pred))

2.3 支持向量机（SVM）

• 原理： 在高维空间找到一个超平面，将数据分为不同类别，并最大化两类之间的间隔。
• 核函数：
  • 线性核：适合线性可分数据。
  • RBF核：适合非线性数据。
• 优缺点：
  • 优点：性能稳定，适合小样本高维数据。
  • 缺点：对超参数敏感。

代码实现：

from sklearn.svm import SVC

# SVM模型
svm_model = SVC(kernel='linear')
svm_model.fit(X_train, y_train)

# 预测与评估
y_pred = svm_model.predict(X_test)
print("SVM准确率:", accuracy_score(y_test, y_pred))

3. 模型训练与评估

在机器学习中，模型训练是通过算法从数据中学习规律的过程，而评估是验证模型在未知数据上的表现。以下内容将从训练流程、评估方法和性能指标等方面展开详细解析。

---

3.1 模型训练的基本流程

模型训练的目的是通过已知的输入数据和对应的输出标签，构建一个能够对未知数据进行预测的模型。

        3.1.1 数据集划分

        为了避免模型在训练数据上过拟合（即在新数据上表现较差），我们通常将数据集划分为训练集、验证集和测试集：

• 训练集（Training Set）： 用于模型学习。
• 验证集（Validation Set）： 用于调整模型参数（如超参数）。
• 测试集（Test Set）： 用于最终评估模型性能。

3.2 模型训练

在训练阶段，模型通过优化算法（如梯度下降）最小化损失函数，从而找到最佳参数。

        3.2.1 逻辑回归模型训练

        逻辑回归是一种简单但有效的分类算法，适合线性可分的数据。

        3.2.2 随机森林模型训练

        随机森林是一种集成学习方法，适合处理非线性问题和高维数据。

3.3 模型评估

模型评估是衡量模型在测试数据上的表现，主要通过以下几种指标进行分析。

3.3.1 性能指标

3.3.2 混淆矩阵

混淆矩阵是一种可视化工具，用于显示模型预测的结果分布，包括TP、FP、FN和TN：

• TP（True Positive）： 实际为正，预测也为正。
• FP（False Positive）： 实际为负，预测为正。
• FN（False Negative）： 实际为正，预测为负。
• TN（True Negative）： 实际为负，预测也为负。

3.4 模型对比

通过不同算法的训练与评估，可以对比模型的性能，选择最优模型。例如：

• 逻辑回归可能在简单的线性分类问题上表现良好。
• 随机森林能处理更复杂的非线性问题，并对缺失值更具鲁棒性。