1.概念回顾与新增
二叉树是一种数据结构,其中每个节点最多有两个子节点,分别是左子节点和右子节点。二叉树的链式结构表示是使用指针(或引用)来连接节点,形成树形结构。每个节点包含一个数据元素和两个指向子节点的指针。
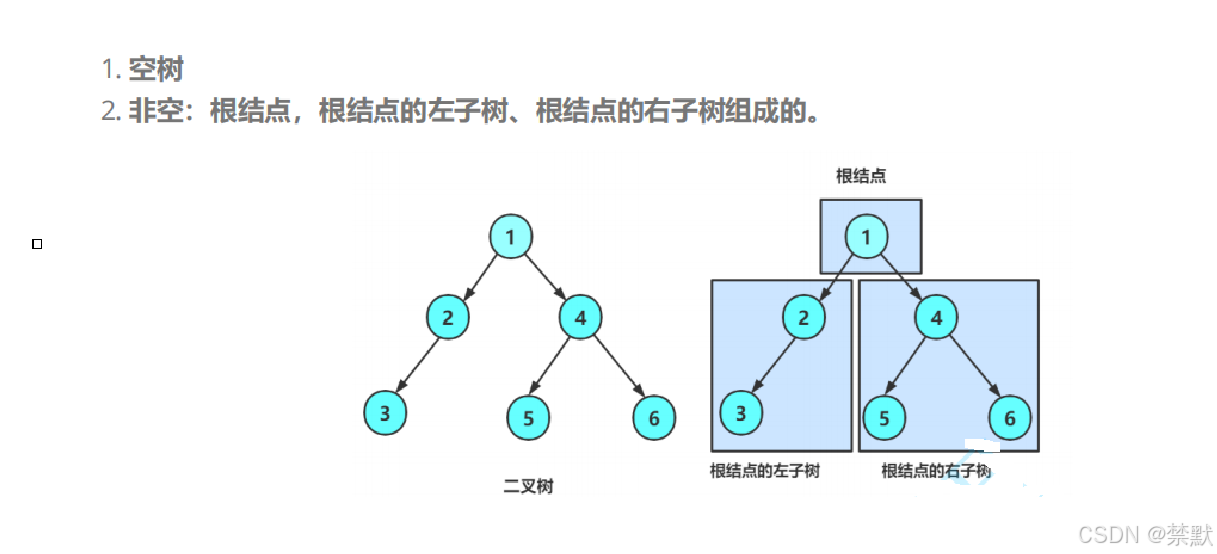
2.简单创建二叉树
分为节点的定义,创建节点,创建树
下面我们将简单的手撕一个二叉树:
typedef struct BTnode {
int val;
struct BTnode* left;
struct BTnode* right;
}Node;
//节点创建
Node* BuyNode(int x) {
Node* node = (Node*)malloc(sizeof(Node));
if (node == NULL) {
perror("node fail");
return NULL;
}
node->val = x;
node->left = NULL;
node->right = NULL;
return node;
}
//树的创建
Node* CreatTree() {
Node* node1 = BuyNode(1);
Node* node2 = BuyNode(2);
Node* node3 = BuyNode(3);
Node* node4 = BuyNode(4);
Node* node5 = BuyNode(5);
Node* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}3.二叉树的遍历
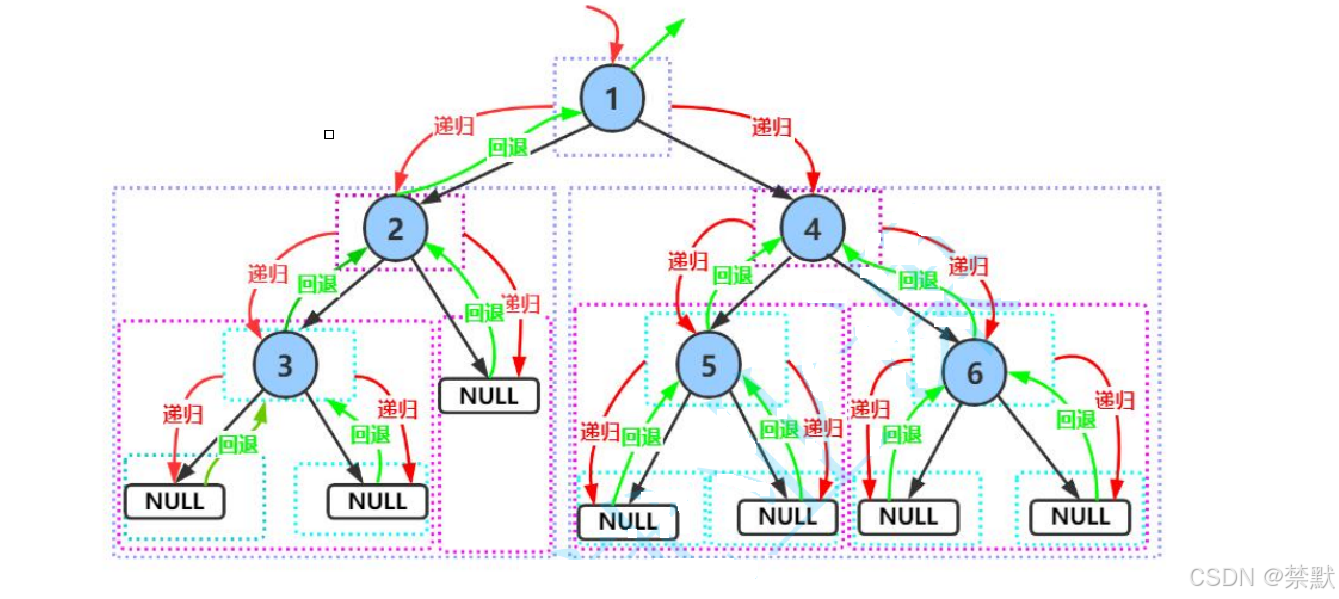
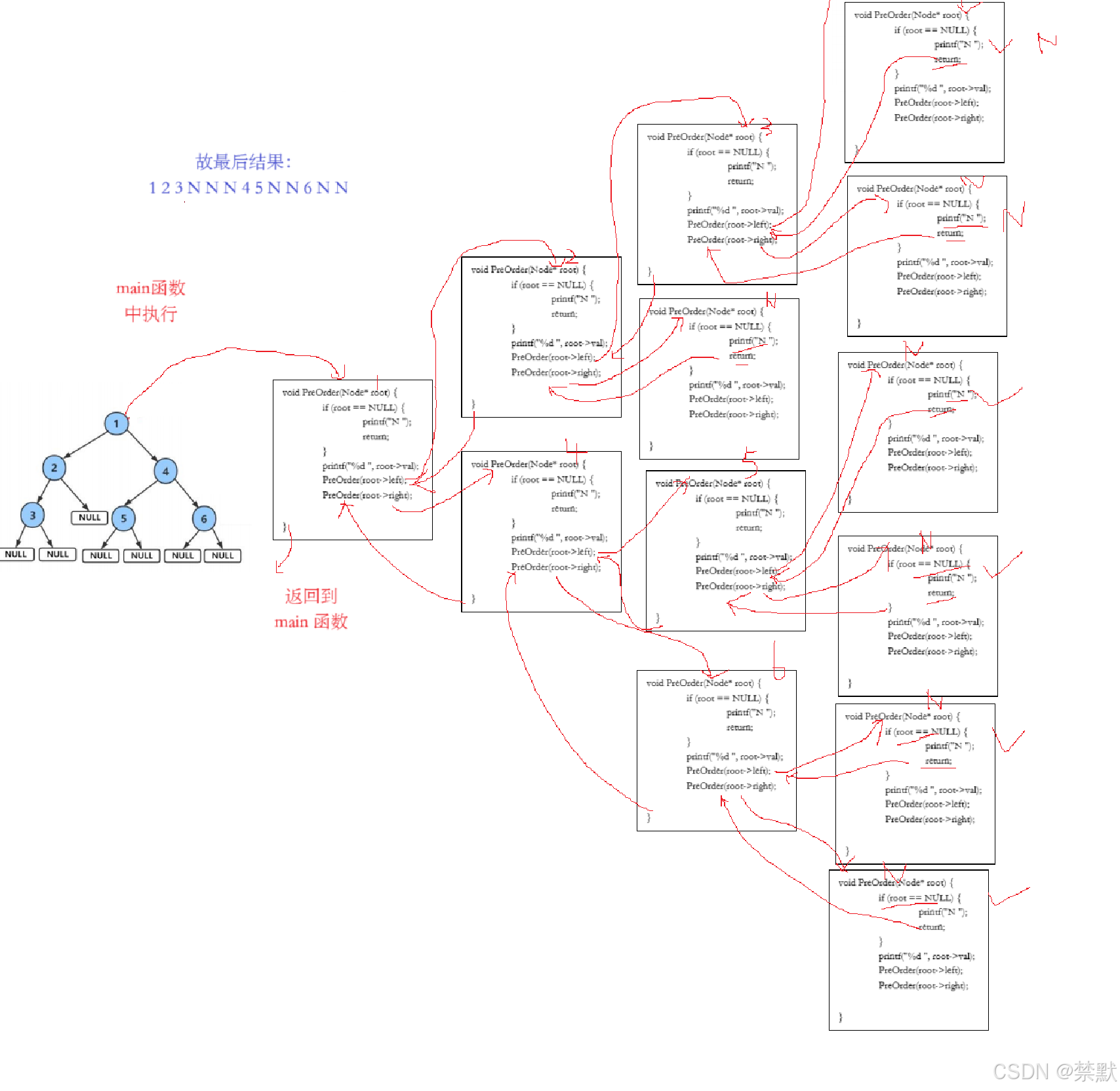
3.1前序遍历
void PreOrder(Node* root) {
if (root == NULL) {
printf("N ");
return;
}
printf("%d ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}
3.2中序遍历
void InOrder(Node* root) {
if (root == NULL) {
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}运行结果:N 3 N 2 N 1 N 5 N 4 N 6 N
3.3后序遍历
void PostOrder(Node* root) {
if (root == NULL) {
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}运行结果:N N 3 N 2 N N 5 N N 6 4 1
3.4层序遍历
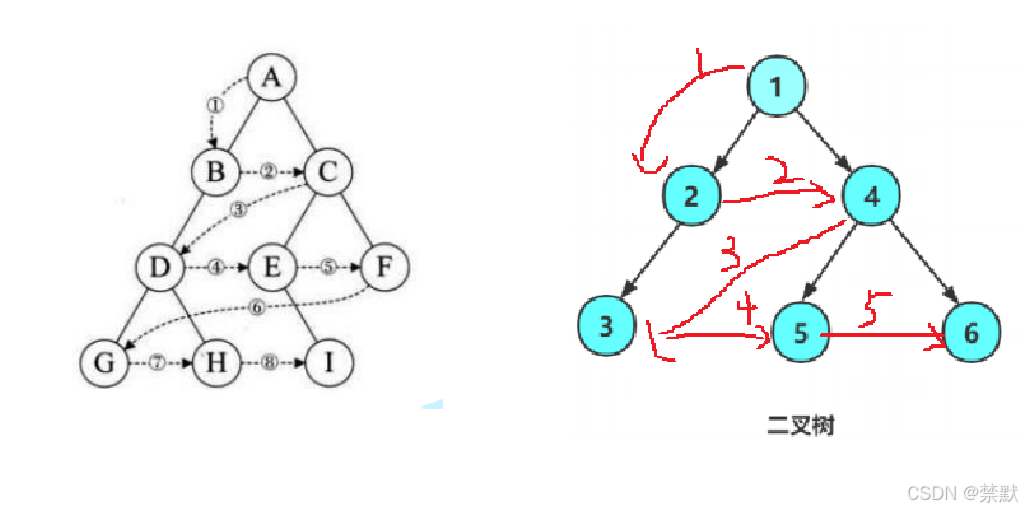
3.4.1队列的实现
// 队列结构
typedef struct Queue {
Node* data[MAX];
int front;
int rear;
} Queue;
// 初始化队列
void initQueue(Queue* q) {
q->front = 0;
q->rear = 0;
}
// 入队
void enqueue(Queue* q, Node* node) {
if ((q->rear + 1) % MAX == q->front) {
printf("Queue is full\n");
return;
}
q->data[q->rear] = node;
q->rear = (q->rear + 1) % MAX;
}
// 出队
Node* dequeue(Queue* q) {
if (q->front == q->rear) {
printf("Queue is empty\n");
return NULL;
}
Node* node = q->data[q->front];
q->front = (q->front + 1) % MAX;
return node;
}
// 判断队列是否为空
int isEmpty(Queue* q) {
return q->front == q->rear;
}3.4.2层序遍历实现
从根节点开始,将每个节点的值打印出来,并依次将其左子节点和右子节点加入队列。
// 层序遍历函数
void levelOrder(Node* root) {
if (root == NULL) {
return;
}
Queue q;
initQueue(&q);
enqueue(&q, root);
while (!isEmpty(&q)) {
Node* node = dequeue(&q);
printf("%d ", node->val);
if (node->left) {
enqueue(&q, node->left);
}
if (node->right) {
enqueue(&q, node->right);
}
}
}3.5主函数测试代码
int main() {
Node* root = CreatTree();
PreOrder(root);
printf("\n");
InOrder(root);
printf("\n");
PostOrder(root);
printf("\n");
levelOrder(root);
return 0;
}运行结果展示:


