一、递归算法

递归（Recursion）是一种解决问题的思路，其精髓在于将问题分解为规模更小的相同问题，持续分解，直到问题规模小到可以用非常简单直接的方式来解决。递归的问题分解方式非常独特，其算法方面的明显特征就是：在算法流程中调用自身。

在调试递归算法程序的时候经常会碰到这样的错误：RecursionError: maximum recursion depth exceeded in comparison，原因递归的层数太多，但系统调用栈容量是有限的。

递归示意图如下：求1到10内的奇数和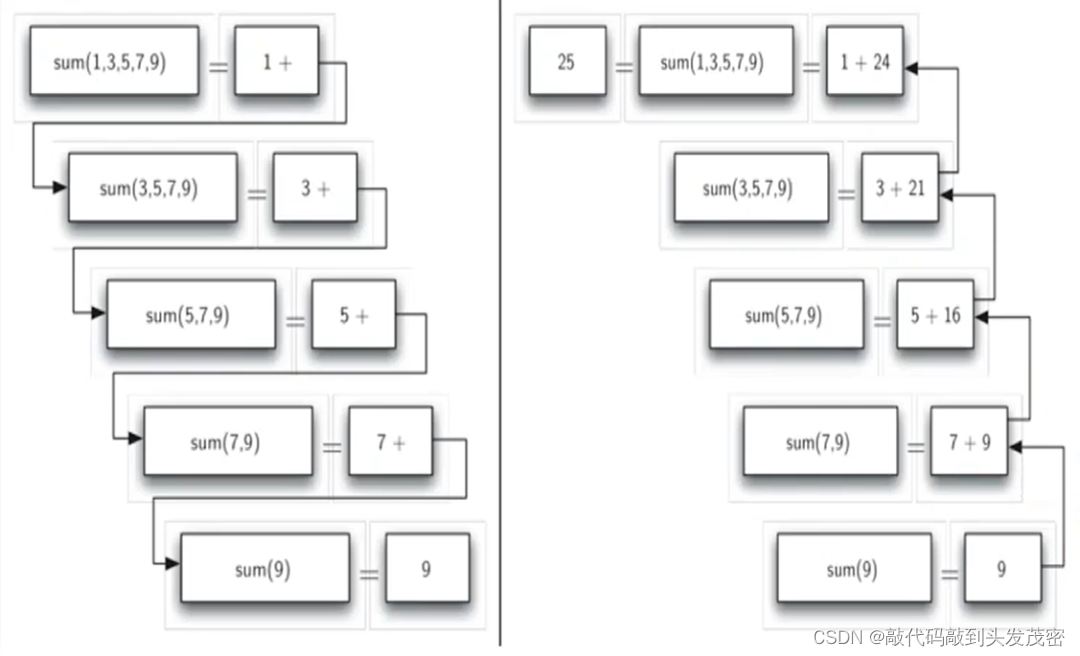

1、什么情况下可以使用递归？

1个问题可以拆分为多个子问题
这些问题求解思路相同，数据规模不同
拥有明确的的终止条件

2、递归算法组成部分

基准条件（递归结束条件）
递归条件
如何分解问题，最终能让递归终止

3、案例：求n的阶乘

基准条件为（结束条件）：函数不在调用自己
递归条件：函数调用自己
如何分解问题：让n在每次执行完之后，都减小

def factorial(n):
    # 基线条件（结束条件）:函数不再调用自己
    if n == 1:
        return 1
    # 递归条件：函数调用自己
    # 让n在每次执行完之后，都变小
    res = n * factorial(n - 1)
    return res

print(factorial(4))

4、编写一个递归函数来计算列表包含的元素数。

基线条件:当列表不为空列表时一直删除，删除到空就停止
递归条件，一直传递被修改的列表，以及最后的累加和的变量
问题如何分解：每累加一个元素，就把这个元素在列表里面去掉

nums=[1,2,3,4]
def list_sum(nums,sum_data=0):
    #基线条件:当列表为空列表一直删除，删除到空就停止
    if len(nums)==0:
        return sum_data
    # 递归条件，一直传递被修改的列表，以及最后的累加和的变量
    # 递归条件,问题如何分解：每累加一个元素，就把这个元素在列表里面去掉
    pop_data=nums.pop()
    sum_data=sum_data+pop_data
    return list_sum(nums,sum_data)

nums=[1,2,3,4]
print(list_sum(nums))

5、通过递归找到列表中最大的数字。

基线条件：当列表不为空列表时，一直删除，删除到空停止
递归条件，一直传递修被修改的列表，以及最大值的变量
问题如何分解：每比对一个元素，就把这个元素在列表中删除

def list_max(nums,max_value=0):
    # 基线条件：当列表为空列表，一直删除，删除到空停止
    if len(nums)==0:
        return max_value
    # 递归条件，一直传递修被修改的列表，以及最大值的变量
    # 递归条件，问题如何分解：每比对一个元素，就把这个元素在列表中删除
    pop_data=nums.pop()
    max_value=max(max_value,pop_data)
    return list_max(nums,max_value)

nums=[1,5,3,4]
print(list_max(nums))

6、通过递归的方式实现二分查找算法。

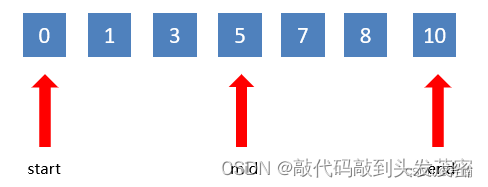
基线条件：当nums[mid]==target时停止；或者当left<=right时停止；
递归条件，一直更新左右指针，并且满足left<=right时
问题如何分解：每次计算mid=(left+right)//2的值后，对nums[mid]与target进行对比，来改变左或者右指针。

二分查找是一种在有序数组中查找元素的算法；将数组分成两部分，判断目标元素可能在哪一部分；直到找到元素或者确定目标元素不存在于数组中。
思路：
1、确定查找范围
2、获取中间元素
3、如果数字小了，就修改最小值
4、如法数字大了，就修改最大值
5、如果猜中了，则返回下标
6、重复以上的过程指导找到目标元素或者u其额定目标元素不存在于数组中

def digui_search(nums,left,right,target):

    while left<=right:
        mid=(left+right)//2
        if nums[mid]==target:
            return mid
        elif nums[mid]>target:
            right=mid-1
            digui_search(nums,left,right,target)
        else:
            left=mid+1
            digui_search(nums,left,right,target)
    return -1
nums=[1,3,5,7,9]
target=2
print(digui_search(nums,0,4,target))

不采用递归的方法，进行二分查找

def binary_search(nums, target):
    # 第一个下标
    low = 0
    # 最后一个下标
    high = len(nums) - 1

    # 只要最小值一直小于最大值，那么就一直循环查找
    while low <= high:
        # 获取中间值的下标值,向下整除
        mid = (low + high) // 2
        if nums[mid] == target:
            return mid
        # 如果中间值小于目标值，修改最小值
        elif nums[mid] < target:
            low = mid + 1
        # 如果中间值大于目标值，修改最大值
        else:
            high = mid - 1
    # 重复以上的过程指导找到目标元素或者u其额定目标元素不存在于数组中
    return -1