算法基础之递归(C++示例)
递归(Recursion),指一种通过重复将问题分解为同类的子问题而解决问题的方法。或者说递归算法是一种直接或者间接地调用自身的算法。简单来说就是一个方法中会重复调用该方法解决问题,直到满足基础部分的条件而输出终止的算法。
特点
(1).递归就是在过程或函数里调用自身。
(2).使用递归算法必须有一个明确的递归结束条件,即递归出口。
经典案例:计算阶乘
一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。1808年,基斯顿·卡曼引进这个表示法。
亦即n!=1×2×3×...×(n-1)×n。阶乘亦可以递归方式定义:0!=1,n!=(n-1)!×n。
源码如下:
#include<iostream>
using namespace std;
int factorial(int n){
if(n==1)
return n;
else
return n*factorial(n-1);
}
int main()
{
int n;
cout<<"请输入整数:";
scanf("%d",&n);
cout<<"整数:"<<n<<"的阶乘为:"<<factorial(n)<<endl;
cout<<"\n"<<endl;
return 0;
}
阶乘的递归算法步骤:
计算4的阶乘factorial(4)时:
1).n=4,首先判断n>2,factorial(4)=4* factorial(3)。
2).计算factorial(3),此时n=3,factorial(3)=3* factorial(2)
3).计算factorial(2),此时n=2,factorial(2)=2。return 2。(递归出口)
合起来的步骤为:
factorial(4)=4* factorial(3)
= 4* 3* factorial(2)
= 4* 3* 2* factorial(1)
= 4* 3* 2* 1=24
经典案例:斐波那契数计算
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
源码如下:
#include<iostream>
using namespace std;
int fib (int n)
{
if (n <= 0) //base case
return 0;
else if (n == 1) //base case
return 1;
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n;
cout<<"请输入斐波那契第几个数:";
scanf("%d",&n);
cout<<"第"<<n<<"个斐波那契数为:"<<fib(n-1)<<endl;
cout<<"\n"<<endl;
}
经典案例:汉诺塔问题
将木块借助B由A柱移动到C柱,每次只能移动一个木块,只能出现小木块在大木块之上。
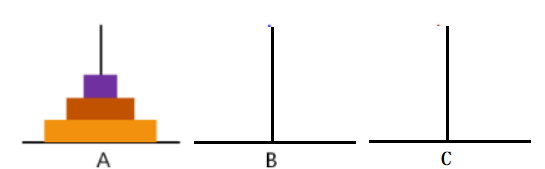
问题分解:
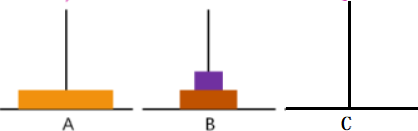
将n-1个木块借助C柱由A柱移动到B柱;
将底层的唯一木块直接移动到C柱;
将n-1个木块借助A柱由B柱移动到C柱;
源码如下:
#include<iostream>
using namespace std;
/*********************************
* a: A柱
* b:B柱
* c:C柱
* n: 木块的数量
* ******************************/
void HanoiTower(char a,char b,char c,int n){
if (n==1) cout<<a<<" -> "<<c<<endl; //直接移动到C柱,输出
else {
HanoiTower(a,c,b,n-1); //将A柱上的n-1个木块借助C柱移动到B柱
cout<<a<<" -> "<<c<<endl; //将A柱上的木块,直接移动到C柱,此句等同HanoiTower(a, b, c, 1);
HanoiTower(b,a,c,n-1); //将B柱上的n-1个木块借助A柱移动到C柱
}
}
int main()
{
int n;
cout<<"请输入木块个数:";
scanf("%d",&n);
HanoiTower( 'A','B','C', n);
}
验证角谷定理
一个自然数,若为偶数,则把它除以2,若为奇数,则把它乘以3加1。经过如此有限次运算后,总可以得到自然数值1。求经过多少次可得到自然数1。如:输入22,输出 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1,STEP=16。
问题分析:递归的终止条件是最后值为1;先输入的数n 进行判断,若 n = 1,则输出1,STEP=1;若输入的数为偶数, 则把它除以2,STEP+=1,接着再判断n的值;若为奇数则乘3加1,STEP+=1,接着继续判断;直到n = 1时停止。
源码如下:
#include<iostream>
using namespace std;
/*递归函数,传入自然数和步数*/
int JiaoGu(int n, int step)
{
/*循环体,实现递归操作,直到自然数n=1时退出*/
while (1)
{
if (n % 2 == 0) //如果n是偶数
{
n = n / 2; //将n除以2之后将值再传给n,再接着判断是偶数还是奇数
cout << n * 2 << "/2=" << n << endl;//输出偶数算式
step += 1;//记录n为偶数时循环次数
/*递归出口,当n=1时输出需要的步数,退出递归*/
if (n == 1)
{
cout <<"共需要的步数(输入的自然数算第一步):STEP="<< step << endl;//输出需要的步数
break;
}
}
else //如果n是奇数
{
n = n * 3 + 1;//将n*3+1再传给n,接着再判断是奇数还是偶数
cout << (n - 1) / 3 << "*3+1=" << n << endl;//输出奇数算式
step += 1;//记录n为奇数的循环次数
}
}
return n;//返回自然数
}
int main()//主函数
{
int n;//自然数
int step=1;//计算需要的步数,从输入的数开始就算第一步
cout << "请输入一个自然数:" ;
cin >> n;//从键盘输入一个自然数,如 32
cout << "过程如下所示:" << endl;
JiaoGu(n, step);//调用递归函数,传入一个自然数与初始步数
}
