重建二叉树

【题目】：

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树，并返回重建后二叉树的根节点。

假设两个遍历的结果中没有重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

【解题思路】：

• 从前序遍历中找到第一个结果作为根节点；
• 在中序遍历中找到这个值，则这个值左边的值是左子节点；右边则是右子节点；
• 利用递归，采用同样的方法重构二叉树。

# Define functions for binary tree
class TreeNode(object):
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None


# preOrder function
def pro_order(root):
    if not root:
        return
    print(root.val, end="->")
    pro_order(root.left)
    pro_order(root.right)


#  inOrder function
def in_order(root):
    if not root:
        return
    in_order(root.left)
    print(root.val, end='->')
    in_order(root.right)


# Construct the binary tree
def construct_binary_tree(pro_order, in_order):
    if not pro_order or not in_order or len(pro_order) != len(in_order):
        return

    def construct(pro_order, in_order):
        if not pro_order:
            return None

        #  build root node
        root = TreeNode(pro_order[0])

        #  find root node in inorder
        for i in range(len(in_order)):
            if in_order[i] == root.val:
                break

        #  build left tree
        root.left = construct(pro_order[1: len(in_order[:i]) + 1], in_order[:i])
        #  build right tree
        root.right = construct(pro_order[i + 1:], in_order[i + 1:])
        return root

    return construct(pro_order, in_order)


#  test
pre = [1, 2, 4, 7, 3, 5, 6, 8]
ino = [4, 7, 2, 1, 5, 3, 8, 6]
root = construct_binary_tree(pre, ino)
print("PreOrder:")
pro_order(root)
print("None\nInOrder:")
in_order(root)
print("None")

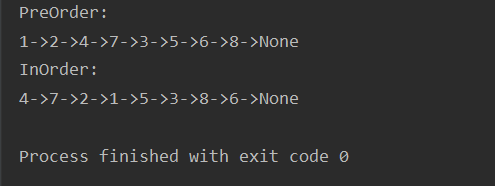
运行结果：

示例代码2：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if (not preorder) and (not inorder) and (len(preorder) == len(inorder)):
            return None
        node = TreeNode(preorder[0])
        index = inorder.index(preorder[0])

        left_pre = preorder[1:index+1]
        left_in = inorder[:index]
        right_pre = preorder[index+1:]
        right_in = inorder[index+1:]
        node.left = self.buildTree(left_pre, left_in)
        node.right = self.buildTree(right_pre, right_in)
        return node