算法基础之分治（C++示例）

分治（Divide and Conquer），字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。
主要思想：当要处理的数据非常多的时候，可以将众多问题先分解成几个小问题，找到求出这几个小问题的方法之后，再找到合适的方法，将子问题解，组合成求整个问题的解法。按照这个思想，如果子问题还是很大的时候，继续将子问题分成更小的子子问题，来进行求解，以此类推，直至可以直接将解求出为止。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，棋盘覆盖问题……

分治排序
把一个数组分成两个数组，然后在把这两个数组再各自分成两个数组，直到数组有两个数，然后比较这两个数，并且合并，排序。
源码如下：

#include <iostream>
using namespace std;
 
/*
* 打印数组
*/
void printArray(int array[],int length)
{
	for (int i = 0; i < length; ++i)
	{
		cout << array[i] << endl;
	}
}
 
/*
* 一个数组从中间分成两个有序数组
* 把这两个有序数组合并成一个有序数组
*/
void merge(int array[],int first,int center,int end)
{
 
	int n1 = center - first + 1;
	int n2 = end - center;
	int L[n1+1];
	int R[n2+1];
	for(int i = 0; i < n1; i++ )
	{
		L[i] = array[first+i];     //得到前面一部分数组
	}
	//printArray(L,n1);
	for(int j = 0; j < n2; j++ )
	{
		R[j] = array[center+j+1]; //得到后面一部分数组
	}
	//printArray(R,n2);
	L[n1] = 1000;    //设置哨兵
	R[n2] = 1000;	 //设置哨兵

	int k1 = 0;
	int k2 = 0;
	for (int k = first; k <= end; ++k)    //把得到的两个数组进行排序合并
	{	
		if(L[k1] <= R[k2])
		{	
			array[k] = L[k1];
			k1 = k1 + 1; 
		}else{
			array[k] = R[k2];
			k2 = k2 + 1; 
		}
	}
}
 
/*
* 分治算法
* 把一个数组从中间分成分开
* 然后进行排序
*/
void merge_sort(int array[],int first,int end)  
{
	if(first < end){
		int center = (first + end)/2;     //得到中间数
		merge_sort(array,first,center);   
		merge_sort(array,center+1,end);
		merge(array,first,center,end);
	}
}
 
int main(int argc, char const *argv[])
{
	int array[12] = {0,6,1,2,3,7,8,9,4,5,11,10};

	merge_sort(array,0,12);
	printArray(array,12);  // 

	return 0;
}

棋盘覆盖问题
• 在一个2^k * 2^k个方格组成的棋盘中，若恰有一个方格与其他方格不同，则称该方格为一特殊方格，且称该棋盘为一特殊棋盘。
• 显然，特殊方格在棋盘上出现的位置有4^k种情形。因而对任何 k >= 0，有4^k种特殊棋盘。
• 图1中的特殊棋盘是k=2时16个特殊棋盘中的一个。

问题描述
• 在棋盘覆盖问题中，要用图2所示的4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。易知，在任何一个2^k * 2^k的棋盘覆盖中，用到的L型骨牌个数恰为（4^k-1）/3。
基本思想
• 用分治策略，可以设计解棋盘覆盖问题的一个简捷的算法。

1. 当k>0时，将2^k * 2^k棋盘分割为4个2^k-1 * 2^k-1子棋盘，如图3-a所示。特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。
2. 为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，如图3-b所示，这3个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题转化为4个较小规模的棋盘覆盖问题。
3. 递归地使用这种分割，直至棋盘简化为1x1棋盘。

分治算法C++源码如下：

#include <iostream>     
using namespace std;

#define N 4		// 棋盘行（列）数  2^k ,k=2时
int tile = 1;	// 骨牌编号
int Board[N][N];// 棋盘

/*
	tr : 棋盘左上角的行号；（从0开始编号） 
	tc : 棋盘左上角的列号；
	dr : 特殊方格左上角的行号；
	dc : 特殊方格左上角的列号；
	size ：size = 2^k 棋盘规格为2^k*2^k
 */
void ChessBoard(int tr, int tc, int dr, int dc, int size)
{
	if (size == 1)
		return;

	int t = tile++;		// L型骨牌编号
	int s = size / 2;	// 分割棋盘

	// 覆盖左上角子棋盘
	// 特殊方格在此棋盘中（下面三个if-else同理）
	if (dr < tr + s && dc < tc + s)
		ChessBoard(tr, tc, dr, dc, s);
	// 此棋盘中无特殊方格（下面三个if-else同理）
	else
	{
		Board[tr + s - 1][tc + s - 1] = t;	// 用编号为t的骨牌覆盖右下角
		ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);	// 覆盖其余方格
	}

	// 覆盖右上角子棋盘
	if (dr < tr + s && dc >= tc + s)
		ChessBoard(tr, tc + s, dr, dc, s);
	else
	{
		Board[tr + s - 1][tc + s] = t;		// 用编号为t的骨牌覆盖左下角
		ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);	// 覆盖其余方格
	}

	// 覆盖左下角子棋盘
	if (dr >= tr + s && dc < tc + s)
		ChessBoard(tr + s, tc, dr, dc, s);
	else
	{
		Board[tr + s][tc + s - 1] = t;		// 用编号为t的骨牌覆盖右上角
		ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);	// 覆盖其余方格
	}

	//覆盖右下角子棋盘
	if (dr >= tr + s && dc >= tc + s)
		ChessBoard(tr + s, tc + s, dr, dc, s);
	else
	{
		Board[tr + s][tc + s] = t;		  // 用编号为t的骨牌覆盖左上角
		ChessBoard(tr + s, tc + s, tr + s, tc + s, s);	//覆盖其余方格
	}

}

int main()
{
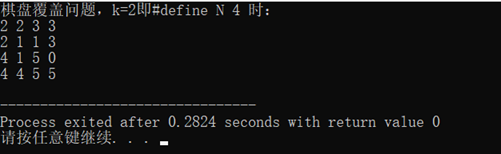
	cout << "棋盘覆盖问题，k=2即#define N 4 时：\n";

	// 将数组（棋盘）所有元素设为0
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++)
			Board[i][j] = 0;

	// 棋盘覆盖
	ChessBoard(0, 0, 2, 3, N);

	// 打印棋盘覆盖情况
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		    {
		   		cout.width(3);    //打印宽度为3
		   		cout << Board[i][j] ;
			}
		cout << endl;
	}
}

运行之结果如下：