前言:本篇文章将继续分享一种新算法——滑动窗口。
长度最小的子数组
给定一个含有
n个正整数的数组和一个正整数target。找出该数组中满足其总和大于等于
target的长度最小的 连续子数组
[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回0。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4] 输出:1示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
意思就是在全是正整数的数组中找到最小的连续的几个数字,它们的和要 >= target。
比如示例一,2,3,1,2这个子数组的和同样满足条件,但是因为有更小的子数组4,3,所以结果为4,3。
那么我们该如何找到那个最小的子数组呢?
借助双指针的思想,定义两个指针均指向数组最左侧,然后左指针不动,让右指针不断向右移动,直到两个指针中间的所有数据的和>=target才停下,这样就能得到一个满足条件的子数组。
当满足条件之后,我们该怎么做呢??让右指针继续右移??当然不是,因为数组中的数据全是正整数,如果右指针继续右移,那么两指针之间的所有数字和仍然>=target,但是此时该子数组的长度变大了,不再满足最小子数组的条件。
所以正确的做法是让left右移,开始寻找另一个子数组,而此时新子数组的数字和,只需要让原子数组的数字和减去left原本指向的数字即可。
如果此时我们把上述过程抽象成图形,就像一个窗口在数组上来回滑动:
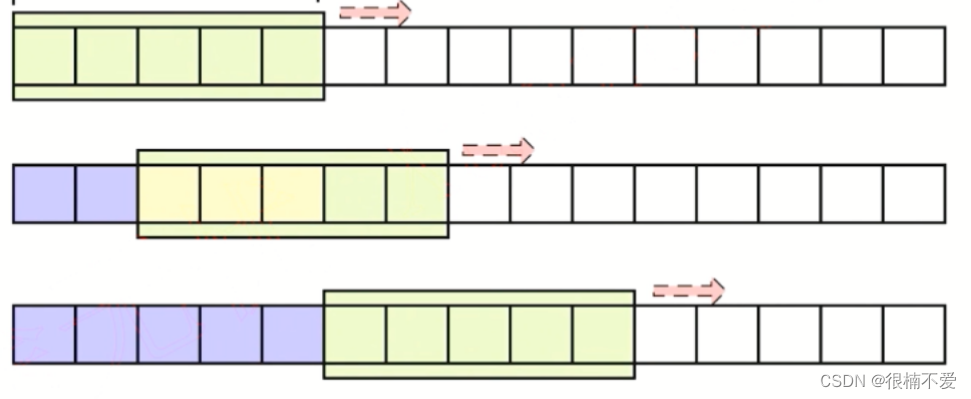
所以滑动窗口即:两个同向移动的指针,而且均不会返回数组开头重新移动,同时还需要要操作的数据具有单调性,比如满足全是正整数。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int left = 0;
int right = 0;
int sum = 0;
int length = INT_MAX;
while(right < nums.size())
{
sum += nums[right];
while(sum >= target)
{
length = min(length,right - left + 1);
sum -= nums[left++];
}
right++;
}
return length == INT_MAX ? 0 : length;
}
};每次找到更小的子数组均进行更新,而循环结束的条件无非就是right向右超出了数组的界限。
总结
像这种需要再数组或者是一段连续的数据中求出满足要求的一端连续的子数组的问题,就可以通过滑动窗口的方法去快速解决。

