一、【模版】前缀和

牛客网—【模版】前缀和

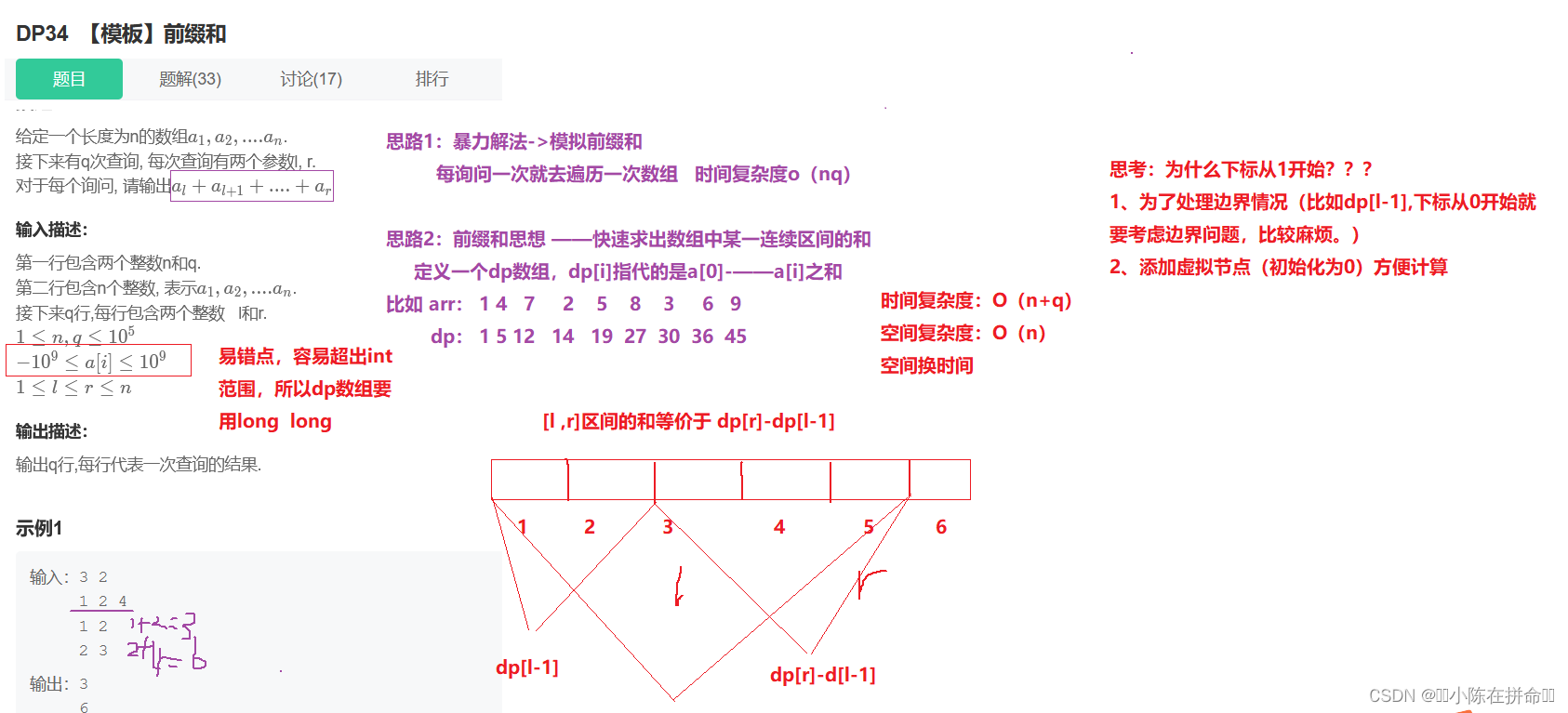
#include<iostream>
#include<vector>
using namespace std;

int main() 
{
  int n,q;
  cin>>n>>q;
  //创建数组 下标从1开始
  vector<int> arr(n+1);
  for(int i=1;i<=n;++i)  cin>>arr[i];   
  //创建一个前缀和数组
  vector<long long> dp(n+1);//默认初始化的时候是0
  for(int i=1;i<=n;++i)  dp[i]=arr[i]+dp[i-1];
  //使用前缀和数组
  int l,r;
  while(q--)
  {
    cin>>l>>r;
    cout<<dp[r]-dp[l-1]<<endl;
  }
  return 0;
}

二、【模板】二维前缀和

牛客网—【模版】二维前缀和

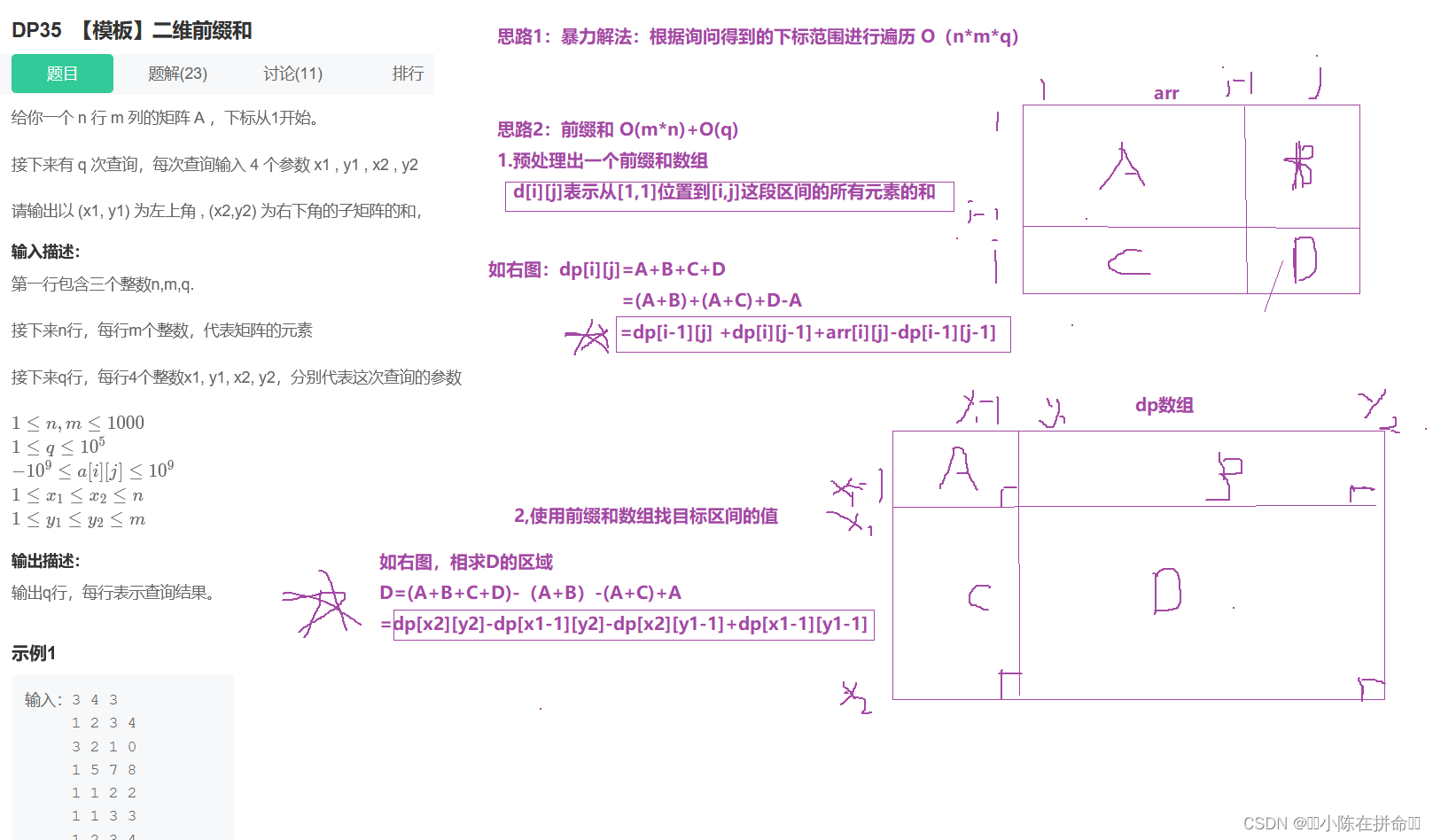
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
   int n,m,q;
   cin>>n>>m>>q;
   //根据m和n创建二维数组 
   vector<vector<int>> arr(n+1,vector<int>(m+1));
   for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) cin>>arr[i][j];
   //创建前缀和矩阵
    vector<vector<long long>> dp(n+1,vector<long long>(m+1));//防止溢出
   for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) 
      dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
   //使用前缀和矩阵
   int x1,y1,x2,y2;
   while(q--)
   {
     cin>>x1>>y1>>x2>>y2;
     cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
   }
}

三、寻找数组的中间下标

. - 力扣（LeetCode）寻找数组的中间下标

class Solution {
public:
    int pivotIndex(vector<int>& nums) 
    {
        int n=nums.size();
         //创建一个前缀和数组
         vector<int>  dpq(n);
         for(int i=1;i<n;++i)  dpq[i]=nums[i-1]+dpq[i-1]; 
         //创建一个后缀和数组
         vector<int>  dph(n);  
         for(int i=n-2;i>=0;--i)  dph[i]=nums[i+1]+dph[i+1]; 
         //使用前缀和和后缀和数组
         for(int i=0;i<n;++i)  if(dpq[i]==dph[i])  return i;
         return -1;
    }
};

四、除自身以外数组的乘积

. - 力扣（LeetCode）除自身以外数组的乘积

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums)
    {
       int n=nums.size();//记录有效个数
       //创建一个前缀乘积数组
       vector<int> dpq(n,1);
       for(int i=1;i<n;++i) dpq[i]=nums[i-1]*dpq[i-1];
       //创建一个后缀乘积数组
       vector<int> dph(n,1); 
       for(int i=n-2;i>=0;--i)  dph[i]=nums[i+1]*dph[i+1];
       //使用这两个数组并创建answer
       vector<int> answer(n);
       for(int i=0;i<n;++i) answer[i]=dpq[i]*dph[i];
       return answer;
    } 
};

五、 和为k的子数组

. - 力扣（LeetCode）

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) 
    {
         unordered_map<int,int> hash;//用来统计前缀和的个数
         hash[0]=1;//默认有一个前缀和为0的数组
         int sum=0;//记录前缀和
         int ret=0;//记录有多少个和为k的子数组
         for(auto e:nums)
         {
            sum+=e;
            if(hash.count(sum-k))  ret+=hash[sum-k];
            ++hash[sum];
         }
         return ret;
    }
};

六、和可被k整除的子数组

. - 力扣（LeetCode）

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) 
    {
      unordered_map<int,int> hash;//用来统计前缀和%k的余数
      hash[0]=1;
      int sum=0;//统计前缀和
      int ret=0;//统计子数的个数
      for(auto e:nums) 
      {
          sum+=e;
          int temp=(sum%k+k)%k;//确保temp为正数
          if(hash[temp]) ret+=hash[temp];//用ret去统计符合要求的子数组个数
          ++hash[temp];//将该sum对应的余数继续存进去
      }
      return ret;
     }
};

七、连续数组

. - 力扣（LeetCode）

class Solution {
public:
    //将数组中为0的改成-1.找到一个最长子数组 其元素和结果恰好为0
    int findMaxLength(vector<int>& nums) 
    {
        unordered_map<int,int> hash;//用来统计前缀和的下标
        hash[0]=-1;//[0,x-1]之间是否有前缀和是sum，如果x=0，那么x-1=-1，也解释了为什么hash[0]=-1
        int sum=0;
        int ret=0;//用来更新最长的长度
        for(int i=0;i<nums.size();++i)  
        {
           sum+=nums[i]==0?-1:1;
           if(hash.count(sum)) ret=max(ret,i-hash[sum]);
           else hash[sum]=i;//只需要存储最早之前的下标就可以了，因为我们要找的是最长的
        }
        return ret;
    }
};

八、最大子数组的和

. - 力扣（LeetCode）

class Solution {
public:
    int maxSubArray(vector<int>& nums) 
    {
       int sum=0,Max=INT_MIN,Min=0;
       for(auto e:nums) 
        {
            sum+=e;
            Max=max(Max,sum-Min);
            Min=min(Min,sum);
        }
        return Max;
    }
};

九、矩阵区域和

. - 力扣（LeetCode）

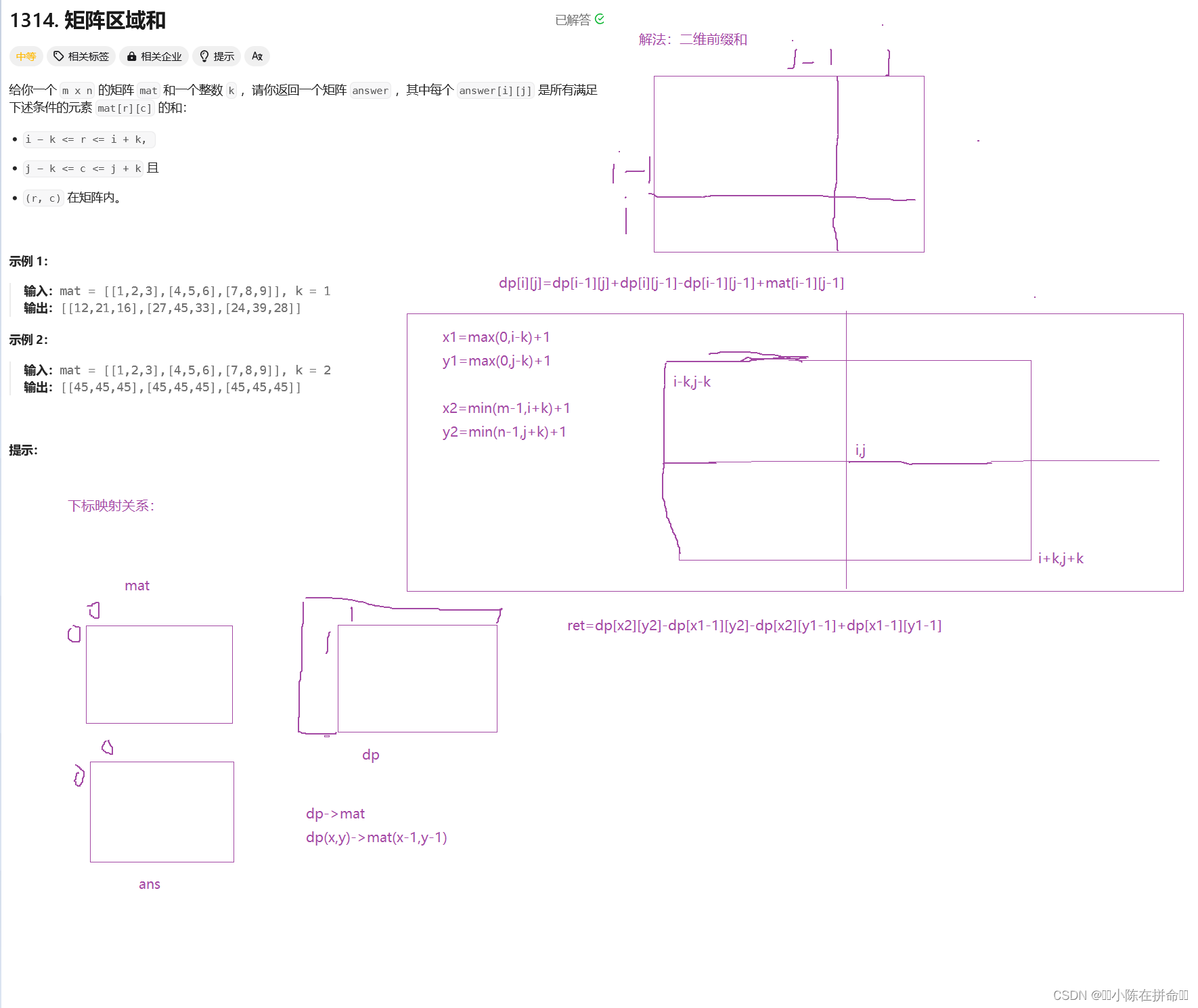
class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) 
    {
        int m=mat.size(),n=mat[0].size();
       //根据矩阵创建一个前缀和数组
       vector<vector<int>> dp(m+1,vector<int>(n+1));
       //开始对矩阵进行值的输入
       for(int i=1;i<=m;++i)
         for(int j=1;j<=n;++j)
            dp[i][j]=dp[i-1][j]+dp[i][j-1]+mat[i-1][j-1]-dp[i-1][j-1];
        //开始使用前缀和数组 输入返回的数组
        vector<vector<int>> answer(m,vector<int>(n));//需要返回的数组
         for(int i=0;i<m;++i)
           for(int j=0;j<n;++j)
             {
                int x1=max(i-k,0)+1,y1=max(j-k,0)+1;
                int x2=min(i+k,m-1)+1,y2=min(j+k,n-1)+1;
               answer[i][j]=dp[x2][y2]+dp[x1-1][y1-1]-dp[x2][y1-1]-dp[x1-1][y2];
             }
             return answer;
    }
};

十、前缀和算法总结

1、前缀和并不一定真的需要搞一个前缀和数组

2、用哈希存前缀和相关数据的话要注意hash[0]

3、无论dp数组是开的n还是开的n+1，都要注意和原数组之间的映射关系。