1.算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢？比如对于以下斐波那契数列：
斐波那契数列的递归实现方式非常简洁，但简洁一定好吗？那该如何衡量其好与坏呢？
long long Fib(int N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}一般通过时间复杂度和空间复杂度
1.2 算法的复杂度
算法在编写成可执行程序后，运行时需要耗费时间资源和空间 ( 内存 ) 资源 。因此 衡量一个算法的好坏，一般 是从时间和空间两个维度来衡量的 ，即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间 。
在计算 机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计 算机的存储容量已经达到了很高的程度。所以如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义：在计算机科学中， 算法的时间复杂度是一个函数 ，它定量描述了该算法的运行时间。一 个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知 道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，
所以才有了时间复杂度这个 分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法 的时间复杂度。
即：找到某条基本语句与问题规模N之间的数学表达式，就是算出了该算法的时间复杂度。
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}Func1 执行的基本操作次数 ： F(N)=N^2+N*2+10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要 大概执行次数，那么这 里我们使用大 O 的渐进表示法。
2.2 大O的渐进表示法
大 O 符号（ Big O notation ）：是用于描述函数渐进行为的数学符号。
推导大 O 阶方法：
1. 用常数 1 取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是 1 ，则去除与这个项目相乘的常数。得到的结果就是大 O 阶。
本质：计算算法时间复杂度（次数）属于哪个量级（level）
使用大 O 的渐进表示法以后， Func1 的时间复杂度为：
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大 O 的渐进表示法 去掉了那些对结果影响不大的项 ，简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数 ( 上界 )
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数 ( 下界 )
例如：在一个长度为 N 数组中搜索一个数据 x
最好情况： 1 次找到
最坏情况： N 次找到
平均情况： N/2 次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为 O(N)
补充：clock
C 库函数 clock_t clock(void) 返回程序执行起（一般为程序的开头），处理器时钟所使用的时间。
可以计算程序的运行时间 ms
#include <stdio.h>
#include <time.h>
int main(){
int begin=clock();
int n=10000000;
int x=10;
for(int i=0;i<n;i++){
++x;
}
int end=clock();
printf("%d\n",x);
printf("%d ms\n",end-begin);
return 0;
}
2.3常见时间复杂度计算举例
实例 1
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}F(N)=2*N+10
基本操作执行了2N+10次，时间复杂度为 O(N)
实例2
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}F(N)=M+N
基本操作执行了M+N次，有两个未知数M和N，时间复杂度为 O(N+M)
若M远大于N,可为O(M),若N远大于M，可为O(N)
实例3
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}基本操作执行了100次，通过推导大O阶方法，时间复杂度为 O(1)
实例4
// 计算strchr的时间复杂度？
const char * strchr ( const char * str, int character );
//底层逻辑
while(*str){
if(*str==character)
return str;
else
++str;
}基本操作执行最好1次，最坏N次，时间复杂度一般看最坏，时间复杂度为 O(N)
实例5
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}基本操作执行最好 N 次，最坏执行了 (N*(N+1)/2 次，通过推导大 O 阶方法 + 时间复杂度一般看最
坏，时间复杂度为 O(N^2)
实例6
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
// [begin, end]：begin和end是左闭右闭区间，因此有=号
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);//防溢出
//int mid=(bigin+end)/2;
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}基本操作执行最好 1 次，最坏 O(logN) 次，时间复杂度为 O(logN)
N/2/2/2/2/.../2=1
假设查找x次->2^x=N->x=log2N
ps ： logN 在算法分析中表示是底 数为2 ，对数为 N 。有些地方会写成 lgN 。
实例 7
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}Fac(N)->Fac(N-1)->Fac(N-2)->...->Fac(0)
计算分析发现基本操作递归了N+1次，时间复杂度为O(N)。
递归时间复杂度：所有递归调用次数累加
实例 8
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}通过计算分析发现基本操作递归了2^N次，时间复杂度为O(2^N)。
累计调用：2^0+2^1+...2^(N-2) =2^(N-1)-1
改进：
long long Fib(size_t n){
long long f1=1;
long long f2=1;
long long f3=0;
for(size_t i=3;i<=N;i++){
f3=f1+f2;
f1=f2;
f2=f3;
}
}时间复杂度：O(N)
若数字太大,也不行，毕竟long long 存储数据有限,可以考虑字符串。
3.空间复杂度
空间复杂度也是一个数学表达式，是对一个算法在运行过程中 临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少 bytes 的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用 大 O 渐进表示法 。
注意： 函数运行时所需要的栈空间 ( 存储参数、局部变量、一些寄存器信息等 ) 在编译期间已经确定好了，因 此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例 1
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}使用了常数个额外空间，所以空间复杂度为 O(1)
实例2
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}动态开辟了N个空间，空间复杂度为 O(N)
实例3
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}递归调用了 N 次，开辟了 N 个栈帧，每个栈帧使用了常数个空间。空间复杂度为 O(N)
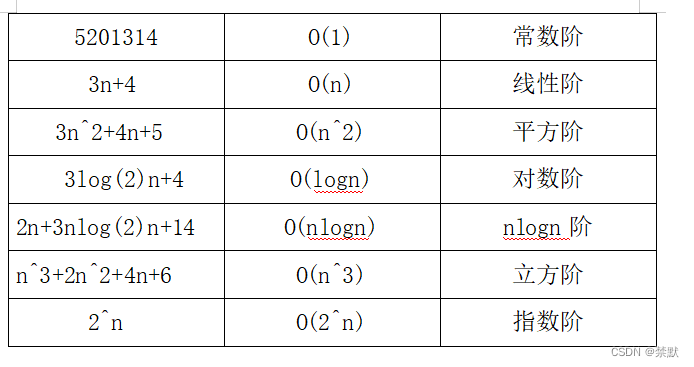
4. 常见复杂度对比
一般算法常见的复杂度如下：
