1. 基本知识
K-Means算法是一种常用的无监督学习算法,旨在将数据集划分为k个簇,使得同一簇内的数据点尽可能接近,而不同簇的数据点尽可能远离
K-Means通过迭代优化质心的位置,最终找到最优的簇划分
K-Means聚类算法的主要步骤如下:
- 选择k个初始质心:从数据集中随机选择k个点作为初始质心
- 分配数据点:将每个数据点分配到最近的质心,形成k个簇
- 更新质心:计算每个簇中所有点的平均值,并将质心更新为该均值
- 检查收敛条件:如果质心的位置变化小于设定的阈值(tolerance),或者达到最大迭代次数(max_iter),则算法收敛,结束迭代;否则,回到步骤2
- 重复步骤2-4,直到算法收敛
K-Means算法的目标是最小化所有点到其所属质心的距离总和

| 优点 | 缺点 |
|---|---|
| 简单易懂,容易实现 | 需要预先指定簇的数量k |
| 计算速度快,适合大规模数据集 | 对初始质心敏感,不同的初始质心可能导致不同的聚类结果 |
| 对于球状簇效果较好 | 容易陷入局部最优,无法保证全局最优 |
| 具有较好的可解释性,聚类结果易于理解 | 只能处理线性可分的簇,对复杂形状的簇效果较差 |
| 内存消耗低,对于数据量大但内存有限的情况依然适用 | 对噪声和异常点敏感,可能会导致质心偏移 |
| 可扩展性强,能够应用于增量聚类和大数据处理 | 不适用于发现非凸形状的簇,聚类结果可能会受到簇形状的影响 |
为了克服K-Means的缺点,可以采用以下优化方法:
- K-Means++初始化:通过一种更加巧妙的方式选择初始质心,以提高聚类结果的稳定性和准确性
- 多次运行K-Means:运行K-Means多次,每次选择不同的初始质心,最终选择最优的聚类结果
- 层次聚类结合:先使用层次聚类确定初始质心,再进行K-Means聚类
- Elkan’s K-Means:使用三角不等式加速距离计算,提高K-Means的效率
2. Demo
import random
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
class KMeans:
def __init__(self, n_clusters=2, tolerance=0.0001, max_iter=300):
self.n_clusters = n_clusters
self.tolerance = tolerance
self.max_iter = max_iter
def fit(self, data):
# 初始化质心
self.centers = data[random.sample(range(data.shape[0]), self.n_clusters)]
old_centers = np.copy(self.centers)
for iteration in range(self.max_iter):
# 用KD树来加速最近质心查询
tree = KDTree(self.centers)
labels = [[] for _ in range(self.n_clusters)]
# 将每个点分配到最近的质心
for point in data:
_, index = tree.query(point)
labels[index].append(point)
# 更新质心
for i in range(self.n_clusters):
if labels[i]:
self.centers[i] = np.mean(labels[i], axis=0)
# 检查质心是否收敛
if np.sum(np.abs(self.centers - old_centers)) < self.tolerance * self.n_clusters:
break
old_centers = np.copy(self.centers)
self.fitted = True
def predict(self, data):
if not hasattr(self, 'fitted') or not self.fitted:
raise Exception("Model not fitted yet.")
result = []
tree = KDTree(self.centers)
for point in data:
_, index = tree.query(point)
result.append(index)
return result
# 主函数部分
if __name__ == '__main__':
# 生成示例数据
np.random.seed(42)
data = np.vstack([
np.random.multivariate_normal([1, 1], [[0.1, 0], [0, 0.1]], 100),
np.random.multivariate_normal([5, 5], [[0.1, 0], [0, 0.1]], 100)
])
# 初始化并拟合模型
kmeans = KMeans(n_clusters=2)
kmeans.fit(data)
# 预测数据所属的簇
predictions = kmeans.predict(data)
# 可视化聚类结果
colors = np.array(['r', 'g'])
plt.figure(figsize=(10, 10))
plt.title("Scatter Plot After K-Means Clustering")
plt.scatter(data[:, 0], data[:, 1], c=colors[predictions])
plt.scatter(kmeans.centers[:, 0], kmeans.centers[:, 1], c='b', marker='x', s=100, linewidths=3)
plt.show()
print("Cluster assignments:", predictions)
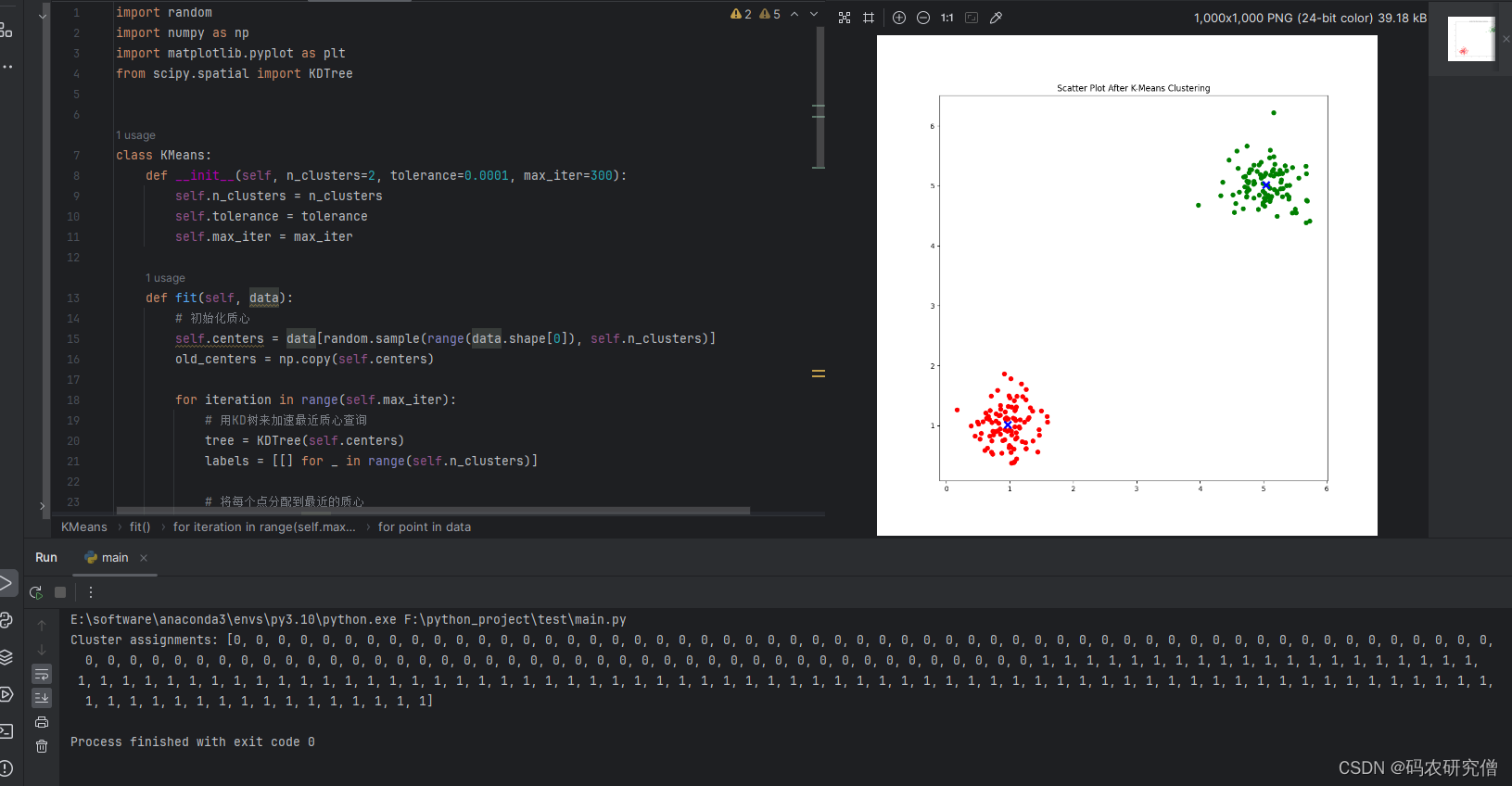
截图如下: