题目：

        给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

 

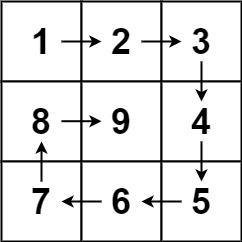
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

分析

        这道题目要求我们生成一个包含从1到 n²的所有元素，且元素按顺时针顺序螺旋排列的n*n正方形矩阵。我们需要注意螺旋顺序的遍历方式，具体来说，我们会扫描矩阵的上边、右边、下边和左边，每次扫描完一条边之后，边界需要进行调整，直到所有的数字都被填入矩阵为止。

示例 1 分析

输入： n = 3

输出： [[1, 2, 3], [8, 9, 4], [7, 6, 5]]

解释： 对于 n = 3，应生成一个 3x3 的矩阵，并从 1 到 9 按照顺时针的顺序依次填充矩阵。

1. 首先，按照顺时针顺序，从左到右填充第一行：1, 2, 3。
2. 然后，从上到下填充最右侧的列：4。
3. 接下来，从右到左填充最后一行：5, 6。
4. 然后，从下到上填充最左侧的列：7, 8。
5. 最后，填充中间的元素 9。

整个过程的填充顺序如下：

1  ->  2  ->  3  
              |
8  <-  9  ->  4
|              |
7  <-  6  <-  5

示例 2 分析

输入： n = 1

输出： [[1]]

解释： 对于 n = 1，仅需要生成一个 1x1 的矩阵，矩阵中只有一个元素，直接填充 1 即可。

提示

范围约束：

1 ≤ n ≤ 20

这意味着输入的 n 的范围是从 1 到 20，包括 1 和 20。

• 最小情况：

  • 当 n = 1 时，生成的矩阵为一种简单的情况，仅包含一个元素 [1]。

• 最大情况：

  • 当 n = 20 时，生成一个 20x20 的矩阵，需要填充从 1 到 400 的所有数字。这种情况下，考察代码的效率和内存使用情况尤为重要。

示例和提示总结

• 示例 1 和 示例 2 展示了小规模的矩阵生成，帮助理解顺时针螺旋填充的逻辑。
• 提示则定义了 n 的取值范围，让我们了解最小和最大情况下的输入范围，确保代码能在这些边界条件下正确运行。

流程图

逐字符匹配过程图示

        我们可以将矩阵看作一个右上方向开的四边形，不断收缩四条边界，依次为上、右、下、左方向进行填充。

例如 n = 3 的情况
起始:
 1. 1→2→3
 2. 8   4
 3. 7←6←5

过程中
  1 → 2 → 3
  ↓        ↓
  8        4
  ← 7 ← 6 ← 5
完成后:

  1 → 2 → 3
  ↓       4
  8       5
  7 ← 6 ← 5

检测并利用循环的过程图示

我们逐步填充每个方向的元素，然后调整边界值，直到所有元素都被填充：

1. 初始状态，设定左、右、上、下四个边界 left=0, right=n-1, top=0, bottom=n-1。
2. 依次填充上边、右边、下边、左边：
   1. 上边从 left 到 right
   2. 右边从 top 到 bottom
   3. 下边从 right 到 left
   4. 左边从 bottom 到 top
3. 每完成一步，调整相应的边界：
   1. 填完上边后， top++
   2. 填完右边后， right--
   3. 填完下边后， bottom--
   4. 填完左边后， left++

代码优化及实现

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];
        int num = 1;
        // 定义四个边界变量
        int left = 0, right = n - 1, top = 0, bottom = n - 1;

        while (num <= n * n) {
            // 从左到右填充上边
            for (int i = left; i <= right; i++) {
                matrix[top][i] = num++;
            }
            top++;
            
            // 从上到下填充右边
            for (int i = top; i <= bottom; i++) {
                matrix[i][right] = num++;
            }
            right--;
            
            // 从右到左填充下边
            for (int i = right; i >= left; i--) {
                matrix[bottom][i] = num++;
            }
            bottom--;
            
            // 从下到上填充左边
            for (int i = bottom; i >= top; i--) {
                matrix[i][left] = num++;
            }
            left++;
        }

        return matrix;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int n = 3;
        int[][] matrix = solution.generateMatrix(n);
        for (int[] row : matrix) {
            for (int num : row) {
                System.out.print(num + " ");
            }
            System.out.println();
        }
    }
}

代码讲解

1. 定义四个边界变量 left, right, top, bottom 分别表示当前未填充区域的左、右、上、下边界。
2. 利用 while 循环进行填充，每次填充一个方向上的所有元素，并调整相应的边界直到所有元素填充完毕。
3. 内部的四个 for 循环分别用于从左到右、从上到下、从右到左、从下到上的填充，并在每次填充完成后调整相应的边界(上边 top++，右边 right--，下边 bottom--，左边 left++)。
4. 最后输出生成的矩阵。

知识点解析

1. 二维数组的遍历和填充
   通过定义四个方向的边界和变量，我们可以灵活地控制二维数组的遍历和填充顺序。

2. 边界收缩的条件
   每次完成一条边的填充后，我们需要调整对应的边界，这是确保螺旋顺序的关键。

3. 循环条件控制
   通过 while 循环保证填充过程不会越界，并且能够在所有元素填满之前一直顺时针逐个填充。

通过上述代码和讲解，希望大家能够掌握如何按照指定的顺序填充一个二维数组。在实际开发中，这样的题目有助于加深对数组遍历和边界条件控制的理解。

知识点	描述	代码示例
二维数组定义	在Java中定义并初始化一个二维数组。	int[][] matrix = new int[n][n];
循环控制	使用while循环进行条件控制，确保在所有元素填满之前一直循环	while (num <= n * n) { ... }
边界定义	定义并初始化四个边界变量，分别表示左、右、上、下的边界	int left = 0, right = n - 1, top = 0, bottom = n - 1;
方向遍历	使用for循环按照顺时针方向遍历四条边	for (int i = left; i <= right; i++) { matrix[top][i] = num++; }
边界调整	填充完一条边后，调整相应的边界值	top++;, right--;, bottom--;, left++;
数据填充	在矩阵中按照顺时针顺序插入数据	matrix[top][i] = num++;
方法定义	定义一个生成螺旋矩阵的方法	public int[][] generateMatrix(int n) { ... }
主方法	在main方法中调用生成矩阵的方法并打印结果	public static void main(String[] args) { ... }
嵌套循环	使用嵌套循环遍历并打印二维数组的值	for (int[] row : matrix) { for (int num : row) { ...