分位数回归也是数理统计里面经典的模型，他相对于在最小二乘模型上进行了改进，虽然本身还是线性的参数模型，但对损失函数进行了改进。我们都知道最小二乘的损失函数是均方误差最小，分位数的损失函数是：

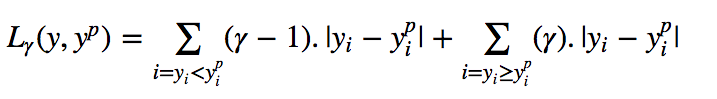
可以看到分位数损失函数会对高估的值和低估的值给予一个不同的权重，这样就可以做到‘’分位‘’。

该模型对于存在异方差的数据有很好的的效果。能准确计算出5%~95%的置信区间

具体看代码理解：

导入包，加载自带的案例数据

import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

data = sm.datasets.engel.load_pandas().data
data.head()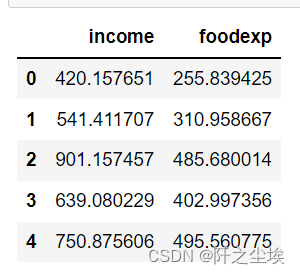

 

 X是收入，y是食物支出，很经典的发散数据，因为不同收入区间的家庭的食物支出比例不一样，随着X增大，Y的波动也增大。存在异方差。

---

q=0.5时候的分位数回归

mod = smf.quantreg("foodexp ~ income", data)
res = mod.fit(q=0.5)
print(res.summary())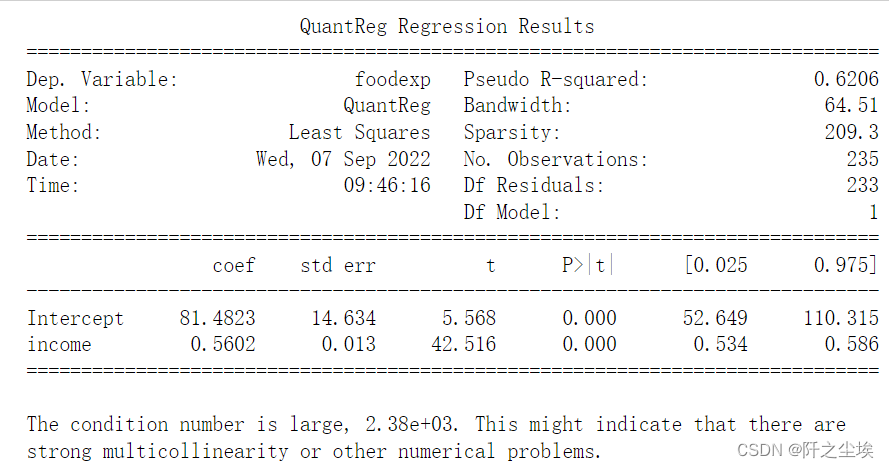

 当q不一样是回归出来的系数是不一样的。我们计算0.05,0.15,0.25.....0.95分位数出来的回归系数，还有最小二乘的回归系数。

quantiles = np.arange(0.05, 0.96, 0.1)
def fit_model(q):
    res = mod.fit(q=q)
    return [q, res.params["Intercept"], res.params["income"]] + res.conf_int().loc["income"].tolist()

models = [fit_model(x) for x in quantiles]
models = pd.DataFrame(models, columns=["q", "a", "b", "lb", "ub"])

ols = smf.ols("foodexp ~ income", data).fit()
ols_ci = ols.conf_int().loc["income"].tolist()
ols = dict(a=ols.params["Intercept"], b=ols.params["income"], lb=ols_ci[0], ub=ols_ci[1])

print(models)
print(ols)

画图对比

x = np.arange(data.income.min(), data.income.max(), 50)
get_y = lambda a, b: a + b * x

fig, ax = plt.subplots(figsize=(6, 4))

for i in range(models.shape[0]):
    y = get_y(models.a[i], models.b[i])
    ax.plot(x, y, line, color="grey")

y = get_y(ols["a"], ols["b"])
ax.plot(x, y, color="red", label="OLS")
ax.scatter(data.income, data.foodexp, alpha=0.2)
ax.set_xlim((200, 3000))
ax.set_ylim((200, 2000))
legend = ax.legend()
ax.set_xlabel("Income", fontsize=16)
ax.set_ylabel("Food expenditure", fontsize=16)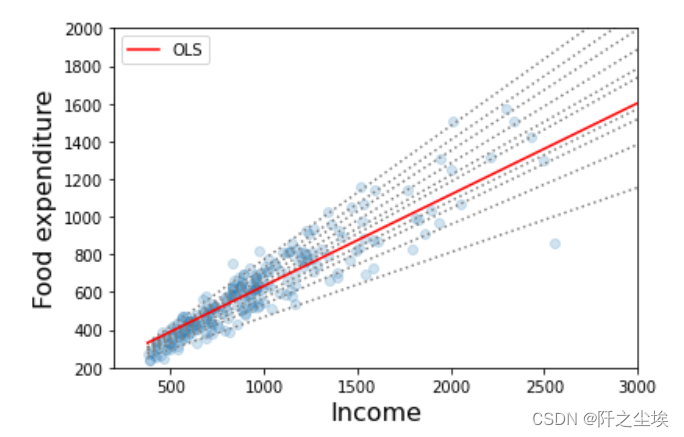

 透明蓝色散点为样本点。蓝色虚线为不同分位数上的回归方程。

可以看出的几个结论：

'''粮食支出随着收入的增加而增加

粮食支出的分散度随着收入的增加而增加

最小二乘估计值与低收入观测值的拟合度相当差（即OLS线越过大多数低收入家庭）'''

而且5%~95%的回归方程区间涵盖了所有的真实样本点，置信区间很准确。

 画出回归系数随着分位数的变化图

n = models.shape[0]
plt.plot(models.q, models.b, color="black", label="Quantile Reg.")
plt.plot(models.q, models.ub, line, color="black")
plt.plot(models.q, models.lb, line, color="black")

plt.plot(models.q, [ols["b"]] * n, color="red", label="OLS")
plt.plot(models.q, [ols["lb"]] * n, line, color="red")
plt.plot(models.q, [ols["ub"]] * n, line, color="red")

plt.ylabel(r"$\beta_{income}$")
plt.xlabel("Quantiles of the conditional food expenditure distribution")
plt.legend()
plt.show()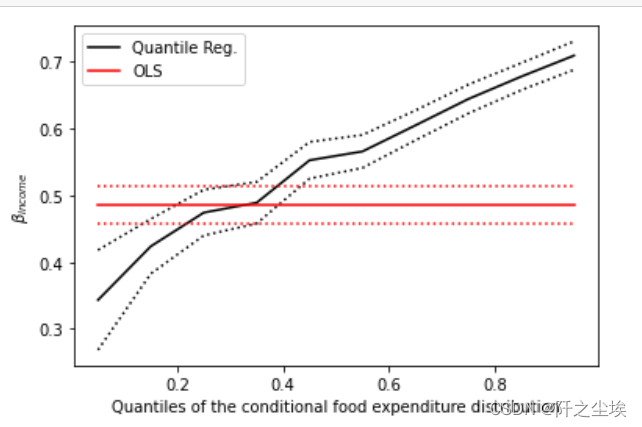

 

#上图画出了回归系数随着分位数的变化而变化，OLS系数是恒定的，分位数回归的系数随着分位数变大而变大

#在大多数情况下，分位数回归点估计值位于OLS置信区间之外，这表明收入对食品支出的影响在整个分布区间内可能不是恒定的