python算法入门
排序
排序算法很多,常见的排序算法:冒泡排序、选择排序、插入排序、归并排序、快速排序、希尔排序、堆排序、计数排序、桶排序、基数排序的思想,在此介绍两种比较好懂的算法。
冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下:
比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
n个元素需要进行n-1次冒泡过程,
def bubble_sort(alist):
for j in range(len(alist)-1,0,-1):
# j表示每次遍历需要比较的次数,是逐渐减小的
for i in range(j):
if alist[i] > alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
li = [54,26,93,17,77,31,44,55,20]
bubble_sort(li)
print(li)
输出结果:[17, 20, 26, 31, 44, 54, 55, 77, 93]
插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
def insert_sort(alist):
# 从第二个位置,即下标为1的元素开始向前插入
for i in range(1, len(alist)):
# 从第i个元素开始向前比较,如果小于前一个元素,交换位置
for j in range(i, 0, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
alist = [54,26,93,17,77,31,44,55,20]
insert_sort(alist)
print(alist)
链表
链表(linked list)种类:单向链表、单向循环链表、双向链表、双向循环链表,在此仅介绍单向链表。
在C/C++中,通常采用“指针+结构体”来实现链表;而在Python中,则可以采用“引用+类”来实现链表。
单向链表
单向链表也叫单链表,是链表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。
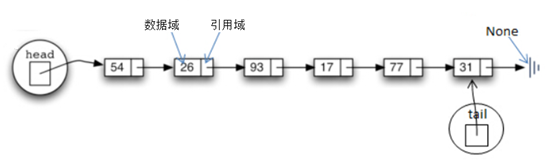
结点(也可以叫节点或元素),每一个结点有两个域,数据域(也叫值域)用于存放用户数据;引用域(也叫指针域)一般是存储着到下一个元素的引用(也叫指针)。
head结点,head是一个特殊的结节,head结点永远指向第一个结点。
tail结点,tail结点也是一个特殊的结点,tail结点永远指向最后一个节点。
None,链表中最后一个结点指针域的指针指向None值,因也叫接地点——所以有些资料上用电气上的接地符号代表None。
☆节点类
python用类来实现链表的数据结构,节点(Node)是实现链表的基本模块,每个节点至少包括两个重要部分:数据域(也叫值域)用于存放用户数据;引用域(也叫指针域)一般是存储着到下一个元素的引用(也叫指针)。
下边的代码用于实现一个Node类:
class Node(object):
def __init__(self, data, next=None):
self.data = data
self.next = next
此节点类只有一个构建函数,接收一个数据参数,其中next表示指针域的指针,实例化后得到一个节点对象,如下:
node = Node(4)
此节点对象数据为4,指针指向None。
☆链表类
先来看LinkedList类的构建函数:
class LinkedList(object):
def __init__(self, head=None, tail=None):
self.head = head
self.tail = tail
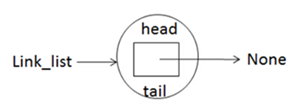
此类实例后会生成一个链表对象,初始化了head和tail节点,且两节点都指向None,实例化代码如下:
link_list = LinkedList()
也可以用图形象的表示这个链表对象,如下:
☆is_empty方法实现
is_empty方法检查链表是否是一个空链表,这个方法只需要检查head节点是否指向None即可,代码如下:
def is_empty(self):
return self.head is None
如果是空列表返回True,否则返回False
☆append方法实现
append方法表示增加元素到链表,这和insert方法不同,前者使新增加的元素成为链表中第一个节点,而后者是根据索引值来判断插入到链表的哪个位置。代码如下:
def append(self, data):
node = Node(data)
if self.head is None:
self.head = node
self.tail = node
else:
self.tail.next = node
self.tail = node
既然要新增加节点,首先把Node类实例化得到一个node对象。这里有两种情况需要考虑,一是链表是一个空链表时怎样append一个节点;二是当链表不是空链表时又怎样append一个节点?
当if self.head is None:为True时,把链表的head和tail都指向了node,假如我们执行了
link_list.append(4)
此时的链表结构如下图:
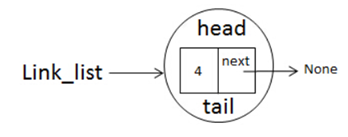
当if self.head is None:为False时,说明链表已经增加了一个节点了,再增加一个节点时head已经指向了第一个节点,所以不为None,比如增加的第二个节点为:
link_list.append(5)
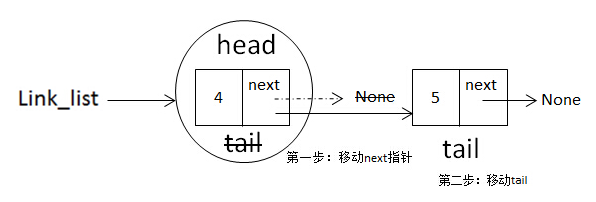
增加第二个节点的操作需要分两步完成,第一步:self.tail.next = node,即把上一个节点的next指针指向当前node;第二步:self.tail = node,把tail移动到node,如下图:

移动完成后就成这样了:
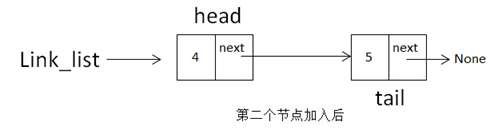
当增加第三个、第四个等节点时,依次类推。
☆iter方法实现
iter方法表示遍历链表。在遍历链表时也要首先考虑空链表的情况。遍历链表时从head开始,直到一个节点的next指向None结束,代码如下:
def iter(self):
if not self.head:
return
cur = self.head
yield cur.data
while cur.next:
cur = cur.next
yield cur.data
当是遍历一个空链表时,if not self.head:为True,直接返回None;如果不是空链表就让一个局部变量cur指向head,并把head的data属性yield出来,再对cur的next指针指向的对象做while循环,直到next指向None,这样就遍历了链表。
☆insert方法实现
假如采取append方法又增加了两个节点,增加完成后如下图:
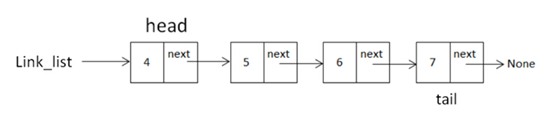
如果想在数据域为6的那节点处插入一个节点,需要做的操作有两步:
把新节点的next指针指向数据域为6的这个节点,即为数据域为5节点的next指向指向的对象
把数据域为5节点的next指针指向新加的节点
注: 这两个步骤不能颠倒,如果颠倒,数据域为6的节点会被丢失,数据域为7的节点不再是链表的节点。
示意图如下:

还要考虑两种情况:
空链表时
插入位置是链表的最后一个节点时,需要移动tail
当是在链表最后一个节点插入时,示意图如下:

要在指定的索引位置插入一个节点,前提是需要找到这个位置,而当找到插入点时,我们并不需要当前节点的信息,而是需要前一个节点的信息,所以代码中巧妙的使用了while cur_idx < idx-1:的方式,这样能使用cur这个变量能指向插入点上一个节点对象。
实现insert方法的代码如下:
ef insert(self, idx, value):
cur = self.head
cur_idx = 0
if cur is None:
raise Exception('The list is an empty list')
while cur_idx < idx-1:
cur = cur.next
if cur is None:
raise Exception('list length less than index')
cur_idx += 1
node = Node(value)
node.next = cur.next
cur.next = node
if node.next is None:
self.tail = node
☆remove方法实现
remove方法接收一个idx参数,表示要删除节点的索引,此方法要考虑以下几种情况:
空链表,直接抛出异常
删除第一个节点时,移动head到删除节点的next指针指向的对象
链表只有一个节点时,把head与tail都指向None即可
删除最后一个节点时,需要移动tail到上一个节点
遍历链表时要判断给定的索引是否大于链表的长度,如果大于则抛出异常信息
请看下边图例:

以下为remove函数的代码:
def remove(self, idx):
cur = self.head
cur_idx = 0
if self.head is None: # 空链表时
raise Exception('The list is an empty list')
while cur_idx < idx-1:
cur = cur.next
if cur is None:
raise Exception('list length less than index')
cur_idx += 1
if idx == 0: # 当删除第一个节点时
self.head = cur.next
cur = cur.next
return
if self.head is self.tail: # 当只有一个节点的链表时
self.head = None
self.tail = None
return
cur.next = cur.next.next
if cur.next is None: # 当删除的节点是链表最后一个节点时
self.tail = cur
☆size函数实现
size函数不接收参数,返回链表中节点的个数,要获得链表的节点个数,必定会遍历链表,直到最后一个节点的next指针指向None时链表遍历完成,遍历时可以用一个累加器来计算节点的个数,如下代码:
def size(self):
current = self.head
count = 0
if current is None:
return 'The list is an empty list'
while current is not None:
count += 1
current = current.next
return count
☆search函数实现
search函数接收一个item参数,表示查找节点中数据域的值。search函数遍历链表,每到一个节点把当前节点的data值与item作比较,最糟糕的情况下会全遍历链表。如果查找到有些数据则返回True,否则返回False,代码如下:
def search(self, item):
current = self.head
found = False
while current is not None and not found:
if current.data == item:
found = True
else:
current = current.next
return found
下面给出一个比较完整链表测试代码
#Node类:
class Node:
def __init__(self, data):
self.data = data
self.next = None
#LinkedList类及调度代码:
class LinkedList:
def __init__(self):
self.head = None
self.tail = None
def is_empty(self):
return self.head is None
def append(self, data):
node = Node(data)
if self.head is None:
self.head = node
self.tail = node
else:
self.tail.next = node
self.tail = node
def iter(self):
if not self.head:
return
cur = self.head
yield cur.data
while cur.next:
cur = cur.next
yield cur.data
def insert(self, idx, value):
cur = self.head
cur_idx = 0
if cur is None: # 判断是否是空链表
raise Exception('The list is an empty list')
while cur_idx < idx - 1: # 遍历链表
cur = cur.next
if cur is None: # 判断是不是最后一个元素
raise Exception('list length less than index')
cur_idx += 1
node = Node(value)
node.next = cur.next
cur.next = node
if node.next is None:
self.tail = node
def remove(self, idx):
cur = self.head
cur_idx = 0
if self.head is None: # 空链表时
raise Exception('The list is an empty list')
while cur_idx < idx - 1:
cur = cur.next
if cur is None:
raise Exception('list length less than index')
cur_idx += 1
if idx == 0: # 当删除第一个节点时
self.head = cur.next
cur = cur.next
return
if self.head is self.tail: # 当只有一个节点的链表时
self.head = None
self.tail = None
return
cur.next = cur.next.next
if cur.next is None: # 当删除的节点是链表最后一个节点时
self.tail = cur
def size(self):
current = self.head
count = 0
if current is None:
return 'The list is an empty list'
while current is not None:
count += 1
current = current.next
return count
def search(self, item):
current = self.head
found = False
while current is not None and not found:
if current.data == item:
found = True
else:
current = current.next
return found
if __name__ == '__main__':
link_list = LinkedList()
for i in range(30):
link_list.append(i)
#print(link_list.is_empty())
link_list.insert(10, 30) #
#link_list.remove(0)
for node in link_list.iter():
print('node is {0}'.format(node))
print(link_list.size())
# print(link_list.search(20))
你可以测试运行之。
最后,给出实现等腰三角形、直角三角形、菱形代码

☆打印等腰三角形代码
for i in range(6):
for k in range(6-1-i):
print(' ',end=' ')
for j in range(2*i+1):
print('*',end=' ')
print()
☆打印直角三角形代码
for i in range(6):
for j in range(i+1):
print("*",end=" ")
print()
☆打印菱形代码
for i in range(5):
for k in range(4 - i):
print(" ", end=" ")
for j in range(2 * i + 1):
print("*", end=" ")
print()
for i in range(4):
for k in range(i + 1):
print(" ", end=" ")
for m in range((7 - 3 * i) + i):
print("*", end=" ")
print()

