85. 最大矩形
给定一个仅包含
0和1、大小为rows x cols的二维二进制矩阵,找出只包含1的最大矩形,并返回其面积。示例 1:
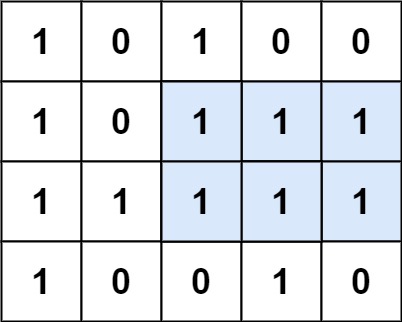
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:6 解释:最大矩形如上图所示。示例 2:
输入:matrix = [["0"]] 输出:0示例 3:
输入:matrix = [["1"]] 输出:1
提示:
rows == matrix.lengthcols == matrix[0].length1 <= row, cols <= 200matrix[i][j]为'0'或'1'
解题思路
关键是利用“柱状图中最大的矩形”问题的解法。我们可以将二维矩阵的每一行视为一个以行为底的柱状图,其中柱子的高度是从当前行向上连续的1的数量。然后,我们可以使用单调栈算法来找到每个柱状图中最大的矩形。通过这种方式,我们逐行处理整个矩阵,最终能够找到只包含1的最大矩形的面积。
具体步骤如下:
- 初始化一个数组
heights,用于存储每一行转换成的柱状图的高度。初始时,heights的长度等于列数cols,所有元素初始化为0。 - 逐行遍历矩阵。对于每一行,更新
heights数组,其中heights[j]表示第j列到当前行为止连续1的个数。 - 对于每一行的
heights数组,使用单调栈算法找出柱状图中最大矩形的面积,并更新最大面积。 - 返回最大面积。
完整代码
Python
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
if not matrix or not matrix[0]:
return 0
max_area = 0
n = len(matrix[0])
heights = [0] * (n + 1) # 加一是为了在最后一列后面添加一个0,方便处理最后一列
for row in matrix:
for i in range(n):
heights[i] = heights[i] + 1 if row[i] == '1' else 0
stack = [-1]
for i in range(n + 1):
while heights[i] < heights[stack[-1]]:
h = heights[stack.pop()]
w = i - 1 - stack[-1]
max_area = max(max_area, h * w)
stack.append(i)
return max_areaJava
public class Solution {
public int maximalRectangle(char[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
int maxArea = 0;
int cols = matrix[0].length;
int[] heights = new int[cols + 1]; // 加一是为了在最后一列后面添加一个0,方便处理最后一列
for (char[] row : matrix) {
for (int i = 0; i < cols; i++) {
heights[i] = row[i] == '1' ? heights[i] + 1 : 0;
}
Stack<Integer> stack = new Stack<>();
stack.push(-1);
for (int i = 0; i <= cols; i++) {
while (stack.peek() != -1 && heights[i] < heights[stack.peek()]) {
int h = heights[stack.pop()];
int w = i - 1 - stack.peek();
maxArea = Math.max(maxArea, h * w);
}
stack.push(i);
}
}
return maxArea;
}
}
86. 分隔链表
给你一个链表的头节点
head和一个特定值x,请你对链表进行分隔,使得所有 小于x的节点都出现在 大于或等于x的节点之前。你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
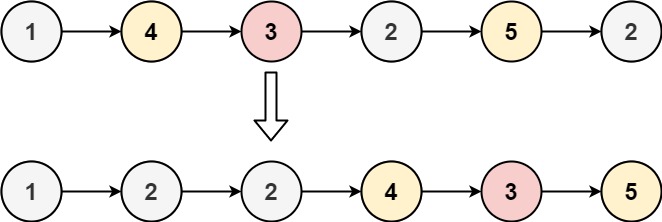
输入:head = [1,4,3,2,5,2], x = 3 输出:[1,2,2,4,3,5]示例 2:
输入:head = [2,1], x = 2 输出:[1,2]
提示:
- 链表中节点的数目在范围
[0, 200]内-100 <= Node.val <= 100-200 <= x <= 200
解题思路
我们可以创建两个新的链表,一个用于存储所有小于 x 的节点,另一个用于存储所有大于或等于 x 的节点。遍历原始链表,根据节点的值将其分配到适当的新链表中。最后,将两个链表合并,使得所有小于 x 的节点都位于前面。
具体步骤如下:
- 创建两个哑节点
beforeHead和afterHead作为两个新链表的头节点。这些哑节点有助于处理边缘情况,使得代码更加简洁。 - 使用两个指针
before和after分别跟踪beforeHead和afterHead链表的当前位置。 - 遍历原始链表。对于每个节点:
- 如果节点的值小于 x,则将其添加到
before链表的末尾,并移动before指针。 - 否则,将节点添加到
after链表的末尾,并移动after指针。
- 如果节点的值小于 x,则将其添加到
- 在遍历完成后,将
after链表连接到before链表的末尾。 - 返回
beforeHead的下一个节点作为新链表的头节点,因为beforeHead是一个哑节点。
完整代码
Python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def partition(self, head: Optional[ListNode], x: int) -> Optional[ListNode]:
beforeHead = ListNode(0)
afterHead = ListNode(0)
before = beforeHead
after = afterHead
while head:
if head.val < x:
before.next = head
before = before.next
else:
after.next = head
after = after.next
head = head.next
after.next = None # 防止成环
before.next = afterHead.next # 连接两个链表
return beforeHead.nextJava
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
public class Solution {
public ListNode partition(ListNode head, int x) {
ListNode beforeHead = new ListNode(0);
ListNode afterHead = new ListNode(0);
ListNode before = beforeHead, after = afterHead;
while (head != null) {
if (head.val < x) {
before.next = head;
before = before.next;
} else {
after.next = head;
after = after.next;
}
head = head.next;
}
after.next = null; // 防止成环
before.next = afterHead.next; // 连接两个链表
return beforeHead.next;
}
}88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组
nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中,使合并后的数组同样按 非递减顺序 排列。注意:最终,合并后数组不应由函数返回,而是存储在数组
nums1中。为了应对这种情况,nums1的初始长度为m + n,其中前m个元素表示应合并的元素,后n个元素为0,应忽略。nums2的长度为n。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
解题思路
要合并两个已经排序的数组 nums1 和 nums2,并保持合并后的数组也是排序的,可以使用双指针的方法从后向前遍历数组,以避免在合并时覆盖 nums1 中未处理的元素。具体步骤如下:
- 初始化两个指针
p1和p2,分别指向nums1和nums2的最后一个元素,即p1 = m - 1和p2 = n - 1。同时,初始化另一个指针p指向合并后的nums1的最后一个位置,即p = m + n - 1。 - 从后向前遍历
nums1和nums2,比较p1和p2指向的元素。将较大的元素复制到p指向的位置,并将对应的指针以及p向前移动一位。 - 如果
p1和p2中有一个先到达数组的开始位置,就将另一个数组剩余的元素直接复制到nums1的前面。 - 继续步骤2和3,直到
p1和p2都遍历完毕。
完整代码
Python
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
p1, p2, p = m - 1, n - 1, m + n - 1
while p1 >= 0 and p2 >= 0:
if nums1[p1] > nums2[p2]:
nums1[p] = nums1[p1]
p1 -= 1
else:
nums1[p] = nums2[p2]
p2 -= 1
p -= 1
# 如果 nums2 还有剩余元素,直接复制到 nums1 的前面
nums1[:p2 + 1] = nums2[:p2 + 1]Java
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = m - 1, p2 = n - 1, p = m + n - 1;
while (p1 >= 0 && p2 >= 0) {
if (nums1[p1] > nums2[p2]) {
nums1[p] = nums1[p1];
p1--;
} else {
nums1[p] = nums2[p2];
p2--;
}
p--;
}
// 如果 nums2 还有剩余元素,直接复制到 nums1 的前面
System.arraycopy(nums2, 0, nums1, 0, p2 + 1);
}
}