169. 多数元素
给定一个大小为
n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数 大于⌊ n/2 ⌋的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3] 输出:3示例 2:
输入:nums = [2,2,1,1,1,2,2] 输出:2
解题思路
- 初始化:创建两个变量,一个用于存储潜在的多数元素(
candidate),另一个用于计数(count)。 - 遍历数组:遍历数组中的每个元素,对于当前元素:
- 如果
count为零,我们假设当前的元素是潜在的多数元素,更新candidate。 - 如果当前元素等于
candidate,增加count。 - 否则,减少
count。
- 如果
- 由于多数元素的定义是出现次数大于
n/2,所以遍历完成后candidate中存储的就是多数元素。
完整代码
Python
class Solution:
def majorityElement(self, nums: List[int]) -> int:
count = 0
candidate = None
for num in nums:
if count == 0:
candidate = num
count += (1 if num == candidate else -1)
return candidateJava
public class Solution {
public int majorityElement(int[] nums) {
int count = 0;
Integer candidate = null;
for (int num : nums) {
if (count == 0) {
candidate = num;
}
count += (num == candidate) ? 1 : -1;
}
return candidate;
}
}
169. 多数元素
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1示例 2:
输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
解题思路
要计算二维网格中岛屿的数量,我们可以采用深度优先搜索(DFS)。对于网格中的每个点,如果它是一个未被访问过的陆地,我们就从这个点开始进行深度优先搜索,将所有与之相连的陆地都标记为已访问,这样就可以找到一个完整的岛屿。我们对网格中的每个点都这样操作,就可以计算出岛屿的总数。
- 遍历网格:对于网格中的每个点,如果它是未被访问的陆地(即值为'1'),则将岛屿数量加一,并对该点进行深度优先搜索。
- 深度优先搜索(DFS):
- 将当前点标记为已访问(即值设为'0'或其他非'1'的值)。
- 检查当前点的四个方向(上、下、左、右),如果相邻的点是陆地(即值为'1'),则对该点递归执行深度优先搜索。
- 重复以上步骤,直到网格中的所有点都被访问过。
完整代码
Python
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
if not grid:
return 0
def dfs(i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == '0':
return
grid[i][j] = '0' # Mark as visited
dfs(i+1, j)
dfs(i-1, j)
dfs(i, j+1)
dfs(i, j-1)
islands = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
dfs(i, j)
islands += 1
return islands
Java
public class Solution {
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int numIslands = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == '1') {
dfs(grid, i, j);
numIslands++;
}
}
}
return numIslands;
}
private void dfs(char[][] grid, int i, int j) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[i].length || grid[i][j] == '0') {
return;
}
grid[i][j] = '0'; // Mark as visited
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
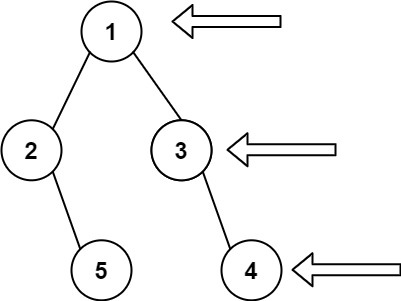
}199. 二叉树的右视图
给定一个二叉树的 根节点
root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4] 输出: [1,3,4]示例 2:
输入: [1,null,3] 输出: [1,3]示例 3:
输入: [] 输出: []
解题思路
- 检查空树:如果根节点为空,则直接返回空列表。
- 初始化:创建一个队列用于层次遍历,初始时只包含根节点。创建一个空列表用于存放结果。
- 层次遍历:
- 对于队列中的每个节点,记录当前层的节点数(即队列的长度)。
- 依次处理当前层的每个节点:将其从队列中移除,并将其子节点(如果有的话)加入队列。
- 将当前层的最后一个节点的值添加到结果列表中。
- 重复上述过程,直到队列为空。
- 返回结果列表。
完整代码
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
result, queue = [], [root]
while queue:
levelLength = len(queue)
for i in range(levelLength):
node = queue.pop(0)
# 如果是当前层的最后一个节点,加入结果列表
if i == levelLength - 1:
result.append(node.val)
# 将子节点加入队列
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return resultJava
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int levelLength = queue.size();
for (int i = 0; i < levelLength; i++) {
TreeNode node = queue.poll();
// 如果是当前层的最后一个节点,加入结果列表
if (i == levelLength - 1) {
result.add(node.val);
}
// 将子节点加入队列
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return result;
}
}