1.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例一：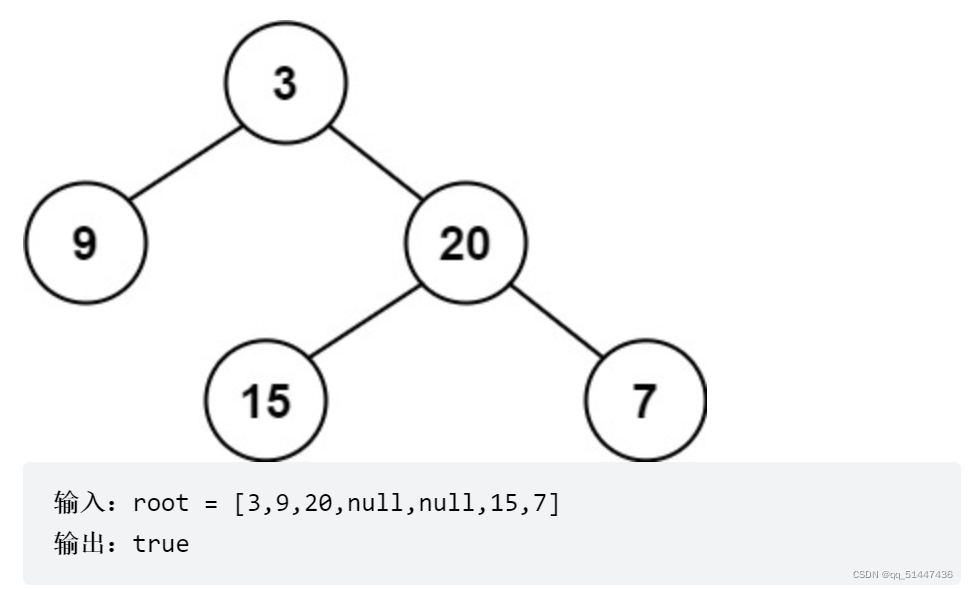

示例二：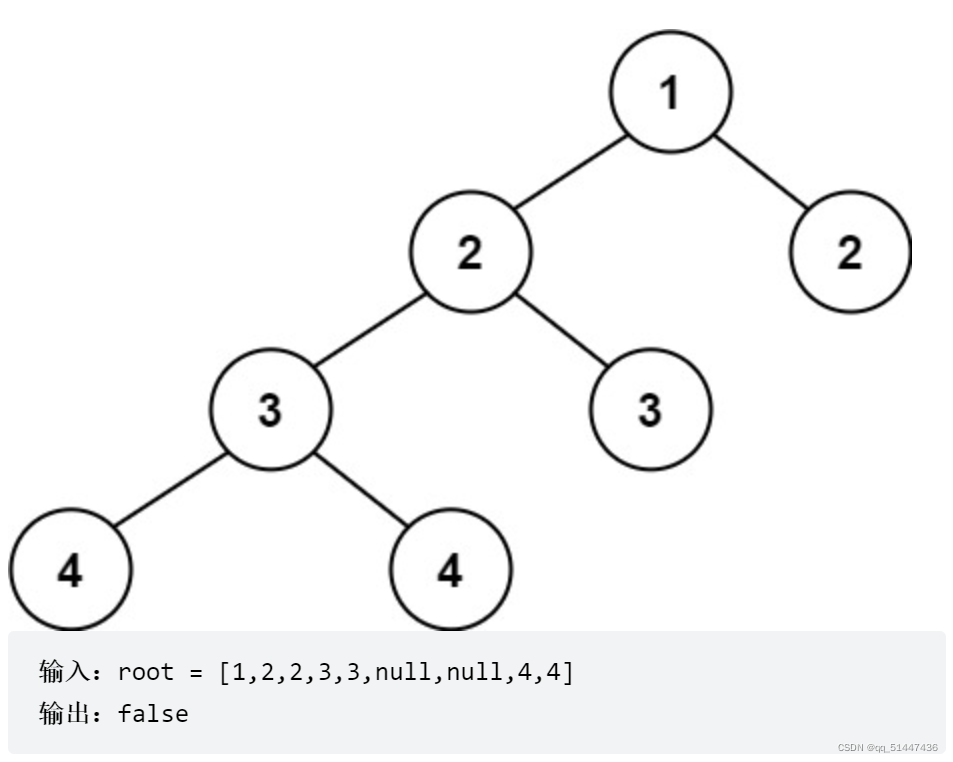

示例三：

1.自顶向上递归求解

该题我们可以用递归的方式求解，如果一个树为平衡二叉树，当且仅当它所有的子树也都是平衡二叉树的时候，那么这个时候该树才为平衡二叉树。
使用自顶向上的求解方法，首先要计算节点的高度，与计算节点的深度类似，具体公式如下所示：
c a c u l a t e H e i g h t ( p ) = { 0 p = n u l l m a x ( c a c u l a t e ( p . l e f t ) , c a c u l a t e ( p . r i g h t ) ) + 1 p ≠ n u l l caculateHeight(p)=\left\{\begin{matrix} 0 & p=null\\ max(caculate(p.left),caculate(p.right))+1 & p \neq null \end{matrix}\right. caculateHeight(p)={0max(caculate(p.left),caculate(p.right))+1​p=nullp​=null​
有了计算节点高度的函数后，我们可以从根节点开始，依次遍历当前节点的左右子树的高度差是否小于等于1，然后分别递归左右子节点，并判断左右子树是否平衡。这是一个自顶向下的递归过程！具体代码如下所示：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }else{
            return Math.abs(caculateHeight(root.left)-caculateHeight(root.right))<=1 &&        isBalanced(root.left) && isBalanced(root.right); 
        }
    }

    public int caculateHeight(TreeNode root){
        if(root==null){
            return 0;
        }else{
            return Math.max(caculateHeight(root.left),caculateHeight(root.right))+1;
        }
    }
}

2.时间复杂度分析

时间复杂度： O ( n 2 ) O(n^2) O(n2)，其中 n 是二叉树中的节点个数。
最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 $O(n)$。
对于节点 p，如果它的高度是 d，则 $\text{height}(p)$最多会被调用 d 次（即遍历到它的每一个祖先节点时）。对于平均的情况，一棵树的高度 h 满足 O ( h ) = O ( l o g 2 n ) O(h)=O(log_{2}n) O(h)=O(log2​n)，因为 $d\le h$，所以总时间复杂度为 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2​n)。对于最坏的情况，二叉树形成链式结构，高度为 O(n)，此时总时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
空间复杂度：$O(n)$，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。代码在LeetCode中的执行效率如下所示：

2.翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例一：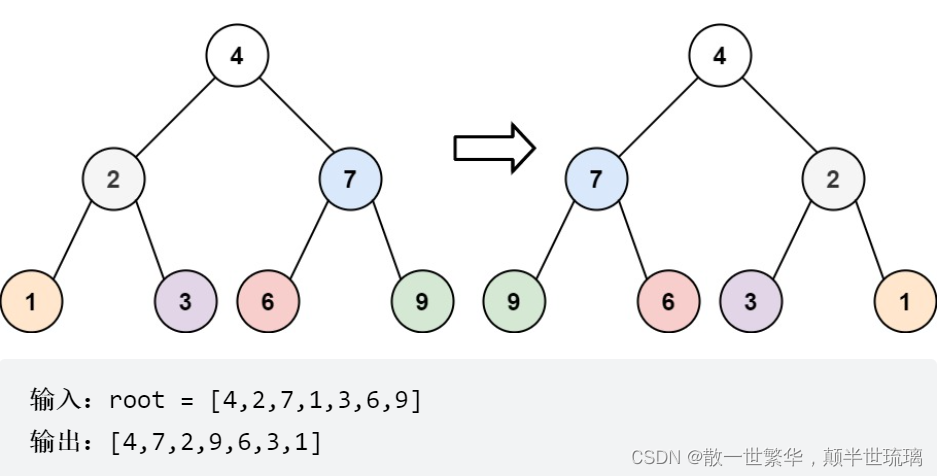

示例二：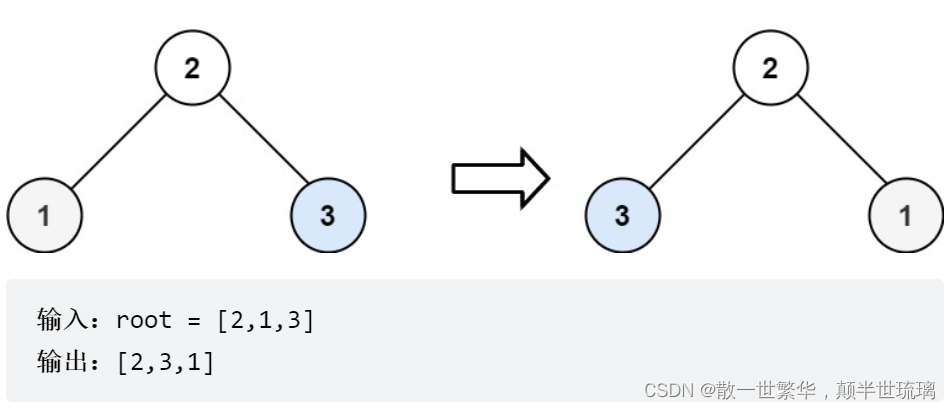

示例三：

1.递归求解

分析题意可知，这里同样可以用递归求解，首先翻转左子树，接下来翻转右子树，最后将翻转后的左右子树交换即可实现翻转二叉树，具体代码实现如下所示：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null){
            return null;
        }
        invertTree(root.left);
        invertTree(root.right);
        TreeNode temp=root.left;
        root.left=root.right;
        root.right=temp;
        return root;
    }
}

2.GIF动图演示

3.时间复杂度分析

时间上，我们遍历二叉树上的每一个节点，因此，时间复杂度为$O(n)$;
空间上，我们使用的空间由递归栈决定，它等于当前二叉树的高度！最坏情况下为$O(n)$;
具体代码在LeetCode中的执行情况如下所示：