1.对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。
示例一：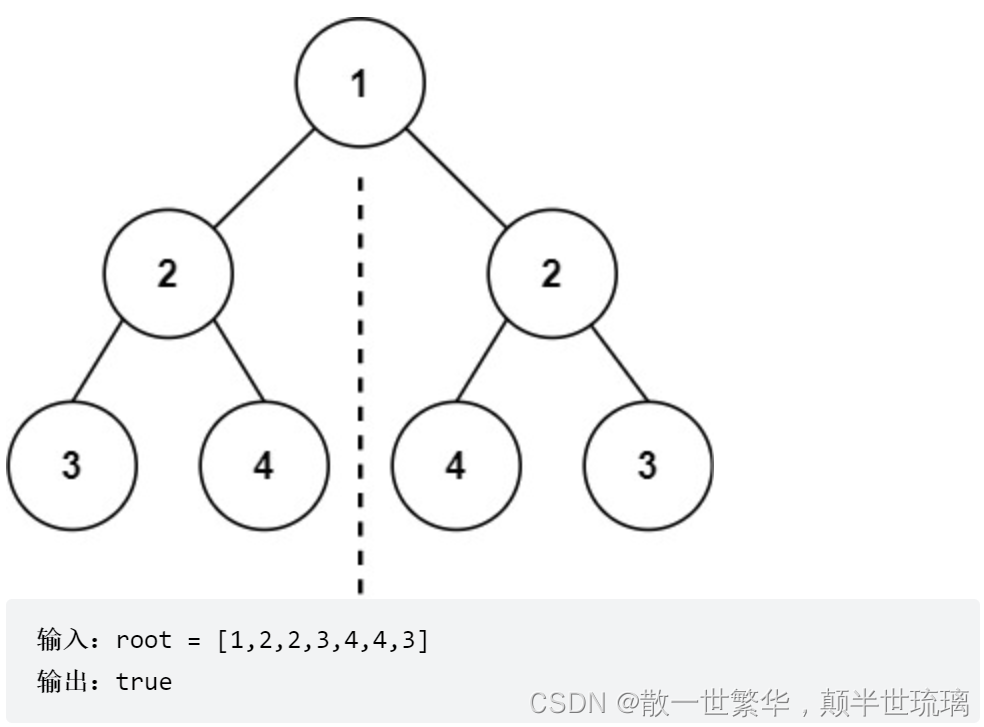

示例二：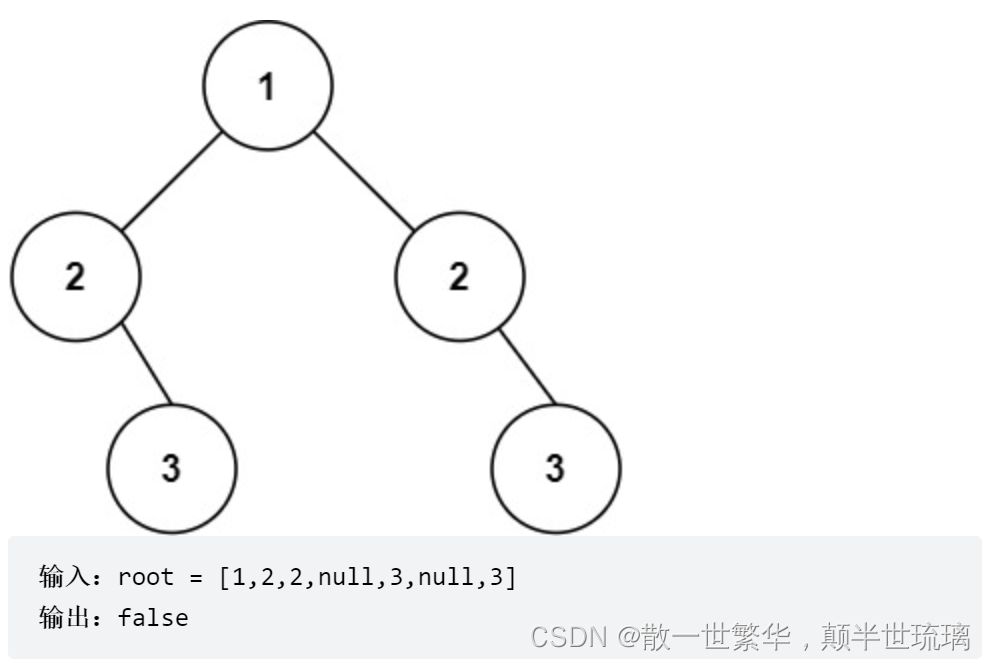

1.递归求解

乍一看无从下手，但用递归其实很好解决。
根据题目的描述，镜像对称，就是左右两边相等，也就是左子树和右子树是相当的。
注意这句话，左子树和右子相等，也就是说要递归的比较左子树和右子树。
我们将根节点的左子树记做 left，右子树记做 right。比较 left.val 是否等于 right.val，不等的话直接返回就可以了。
如果相当，比较 left 的左节点和 right 的右节点，再比较 left 的右节点和 right 的左节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null){
            return true;
        }
        return deepCheck(root.left,root.right);
    }
    boolean deepCheck(TreeNode left,TreeNode right){
        if(left==null && right==null){
            return true;
        }else if(left==null || right==null){
            return false;
        }else if(left.val!=right.val){
            return false;
        }else{
            return deepCheck(left.left,right.right) && deepCheck(left.right,right.left);
        }
    }
}

2.GIF动图演示

下面是一个具体的二叉树递归判断是否为对称二叉树的具体过程。

3.时间复杂度分析

时间复杂度：这里遍历了这棵树，时间复杂度为 O(n)。
空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为 O(n)。具体代码在LeetCode中的执行情况如下所示：

2.二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：

1.递归求解

这里直接递归求解左右子树的最大深度，在二者的最大值的基础上加1返回就是二叉树的最大深度。注意，这里要特别注意递归的出口。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null)
        return 0;
        else{
            return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
        }
    }
}

2.时间复杂度分析

时间复杂度：$O(n)$，其中 $n$ 为二叉树节点的个数。每个节点在递归中只被遍历一次。
空间复杂度：O($\text{height}$)，其中 $\text{height}$表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。
该代码在LeetCode中的执行情况如下所示：