引言
微分方程在物理、工程、经济和生物等多个领域有着广泛的应用。它们用于描述系统中变量与其导数之间的关系,通过这些方程可以解释和预测系统的动态行为。本文将结合MATLAB的数值解法,探讨如何使用MATLAB求解常微分方程和偏微分方程,尤其是刚性与非刚性微分方程问题。通过实际代码示例,帮助读者更好地理解和应用这一重要工具。
微分方程的定义
常微分方程: 常微分方程(Ordinary Differential Equation, ODE)是描述未知函数及其导数之间关系的方程,主要针对一元函数。常微分方程按阶数可以分为一阶、二阶及高阶微分方程。在MATLAB中,常微分方程可以通过符号方法(解析解)和数值方法(数值解)两种方式求解。
偏微分方程: 偏微分方程(Partial Differential Equation, PDE)描述的是多元函数的导数与自变量之间的关系。偏微分方程广泛应用于描述物理场问题,如热传导、电磁场和流体力学中的方程。
MATLAB求解常微分方程
解析解法: MATLAB中的 dsolve 函数用于求解常微分方程和常微分方程组的解析解。当系统存在解析解时,MATLAB可以直接返回结果。例如,考虑一阶常微分方程:
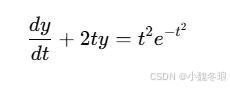
该方程的解可以通过以下命令求得:
syms y(t)
eqn = diff(y,t) + 2*t*y == t^2*exp(-t^2);
sol = dsolve(eqn)
MATLAB将返回方程的通解,若有初始条件,还可返回特解。
参数分析:
- 自变量 ttt:这是方程中的独立变量,如时间等。
- 初始条件:在求解常微分方程时,初始条件是必不可少的。它决定了特定解的唯一性。
- 符号解法的局限:虽然解析解是数学上完美的解法,但许多实际问题无法通过解析方法求解,此时需使用数值方法。
数值解法: 当解析解不可行时,我们通常使用数值解法。在MATLAB中,常用的数值解法包括 ode45、ode23 等方法,这些方法适用于求解一阶和高阶常微分方程。
% 例子:求解 y' = y - 2*t/y
f = @(t, y) y - 2*t/y;
[t, y] = ode45(f, [0 1], 1);
plot(t, y);
此处使用 ode45 函数求解了一个常微分方程,并绘制了解的变化趋势(用MATLAB求解微分方程及微分方程组)(第5讲 用MATLAB求解微分方程及微分方程组)。
MATLAB求解偏微分方程
偏微分方程的求解在工程和物理中非常重要,如描述传热的热传导方程。在MATLAB中,可以通过 pdepe 函数来求解一维时间依赖的偏微分方程组。例如,考虑如下的热传导方程:
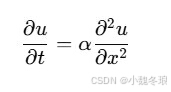
该方程可以用以下MATLAB代码求解:
m = 0; % 0表示一维问题
x = linspace(0,1,20);
t = linspace(0,10,100);
sol = pdepe(m, @pde, @pdeic, @pdebc, x, t);
% 初始条件和边界条件的定义
function u0 = pdeic(x)
u0 = sin(pi*x);
end
function [pl,ql,pr,qr] = pdebc(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = ur;
qr = 0;
end
此代码模拟了一个简单的热传导问题,通过有限差分法近似偏微分方程的数值解。
刚性和非刚性问题
在数值求解微分方程时,刚性问题往往给计算带来挑战。刚性方程的特点是解的某些部分变化非常快,而其他部分变化较慢,标准的数值方法如 ode45 在这种情况下效率较低。此时,可以使用MATLAB中的 ode15s 等专门处理刚性问题的函数。
刚性问题的解决方法: 对于刚性方程, ode15s 是一个多步法的求解器,适用于处理刚性问题。示例:
f = @(t, y) -1000*y + 3000 - 2000*exp(-t);
[t, y] = ode15s(f, [0 1], 0);
plot(t, y);
通过这个示例,我们使用 ode15s 解决了一个刚性方程。
总结
本文详细介绍了使用MATLAB求解常微分方程和偏微分方程的两种主要方法:解析解法和数值解法。解析解法适用于可以求得显式解的方程,而对于无法通过解析法求解的问题,数值解法提供了有效的解决方案。MATLAB中丰富的 ode 系列函数为处理不同类型的微分方程提供了强大的支持。
| 项目 | 内容 |
|---|---|
| 主要问题 | 解决常微分方程(ODE)和偏微分方程(PDE)的解析解和数值解问题,包括刚性和非刚性问题。 |
| 解析解法 | 使用dsolve函数求解ODE的解析解,适用于理论上有显式解的情况,如一阶、二阶常微分方程。 |
| 数值解法 | 对于无法求得解析解的问题,使用ode45、ode23等数值方法,特别是刚性问题可以用ode15s等函数。 |
| 偏微分方程求解 | 使用pdepe函数求解一维时间依赖的PDE问题,广泛应用于热传导等物理问题。 |
| 刚性问题处理 | 刚性问题使用ode15s、ode23s等专门求解器,通过分步求解、提高效率解决快速变化和缓慢变化共存的系统。 |
| 典型代码示例 | 示例代码展示了如何通过ode45求解一阶微分方程,并使用pdepe函数解决PDE问题的数值解。 |
| 应用场景 | 用于物理、工程和数学领域中的动力学模拟,如热传导、物体运动轨迹、化学反应速率等问题。 |
| MATLAB函数 | dsolve(求解析解)ode45、ode23(非刚性问题的数值解)ode15s、ode23s(刚性问题的数值解)pdepe(PDE求解器) |

