1、分治法的基本思想
分治法的基本思想是将一个规模为n的问题分解为k个规模为较小的子问题,这些子问题互相独立且与原问题相同,递归地求解这些子问题,然后利用子问题的解合并出原问题的解。
2、分治算法的设计
分为三个阶段:
- 分解阶段:将整个问题划分为多个子问题。
- 递归求解阶段:求解每个子问题。
- 合并阶段:合并子问题的解,形成原始问题的解。
3、分治算法的分析
分为两个阶段:
- 建立递归方程
- 求解递归方程
4、最大子段和问题
给定由n个整数(可为负数)组成的序列a1,a2.....an,求该序列的子段和的最大值,当所有整数均为负整数时定义最大子段和为0。(子段是连续的)
例:当(a1,a2,a3,a4,a5,a6) = (-2,11,-4,13,-5,-2)时,最大子段和为20(11-4+13)。
下面给出简单的穷举法和分治法求解最大子段和。
穷举法:
int maxsum(int n,int *a,int &besti,int &bestj){//n为长度,a为数组,i为开始位置,j为结束位置
int sum = 0;
for(int i = 1;i <= n;i++){
int thissum = 0;
for(int j = i;j <= n;j++){
thissum += a[j-1];
if(thissum > sum){
sum = thissum;
besti = i;
bestj = j;
}
}
}
return sum;
}时间复杂度:

分治法:
分治算法设计:
如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和。
a[1:n]的最大子段和有三种情形:
- a[1:n]的最大子段和与a[1:n/2]的最大子段和相同。
- a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同。
- a[1:n]的最大子段和为 (从i开始到j结束的子段和),其中1<=i<=n/2,n/2<=j<=n。
其中前两种情况可递归求得,第三种情况a[n/2]与a[n/2+1]在最优子序列中,因此可在a[1:n/2]中计算出最大值,在a[n/2+1:n]中计算出最大值,两者相加为最优解。
int maxsubsum(int *a,int left,int right){
int sum = 0;
if(left == right)//如果只有一个数的情况
return sum = a[left] > 0 ? a[left]:0;
int center = (left+right)/2;
int leftsum = maxsubsum(a,left,center);//第一种情况:左半部分最大值
int rightsum = maxsubsum(a,center+1,right);//第二种情况:右半部分最大值
int s1 = 0;
int lefts = 0;
for(int i = center;i >= left ;i--){
lefts += a[i];
if(lefts > s1)
s1 = lefts;
}
int s2 = 0;
int rights = 0;
for(int i = center+1;i <= right ;i++){
rights += a[i];
if(rights > s2)
s2 = rights;
}
sum = s1+s2;//第三种情况:最大子段和在两者范围连续
if(sum < leftsum) sum = leftsum;
if(sum < rightsum) sum = rightsum;
return sum;
}时间复杂度:
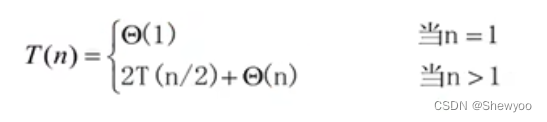
5、循环赛日程表问题
设有n = 2^k个运动员要进行网球循环赛,现在要设计一个满足以下要求的比赛日程表:
①每个选手必须与其它n-1个选手各赛一次。
②每个选手一天只能赛一次。
③循环赛一共进行n-1天。
按此要求,可将比赛日程表设计成有n行和n-1列的一个表,求表中第i行和第j列处填入第i个选手在第j天所遇到的选手。
算法设计:
按分治策略,我们可将所有选手对分为两组,n个选手的比赛日程表就可通过为n/2个选手设计的比赛日程表来决定。递归地用这种一分为二的策略对选手进行分割,直到只剩下2个选手时,只要让这两个选手进行比赛就可以了。
例:
八个选手的比赛日程表:
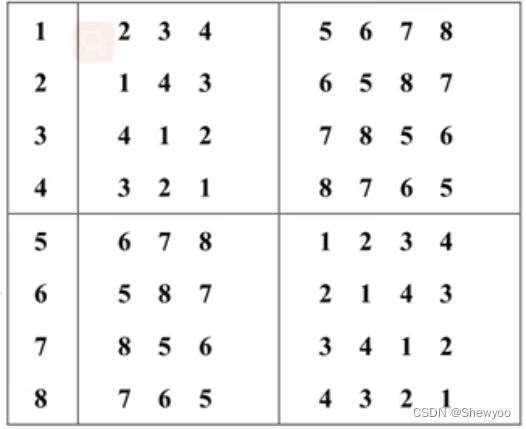
这个8×8的表可以往下划分4×4再往下2×2,如下:
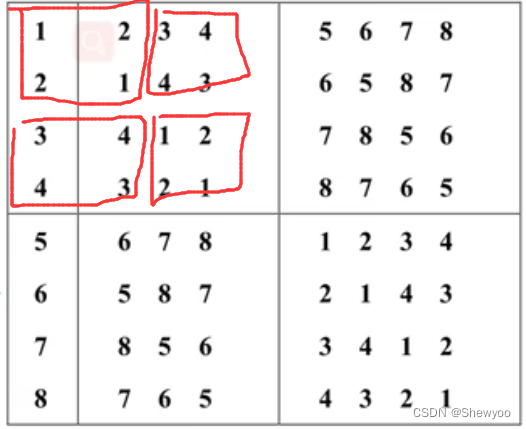
这个表有这么个规律:第一个2×2的矩阵就是12 21,第二个(横向)是第一个矩阵对应的数+n/2(n为当前所处的是n×n矩阵,如上是4×4),第三个第四个矩阵就是对角的矩阵相同。
如果还不懂,再来到8×8的矩阵上来,第二个(横向)矩阵:5 = 1+8/2,6 = 2+8/2......
int matrix[8][8] = {0};//存放日程表数组
void fun(int n){
int i,j;
if(n<=0)return;
if(n > 2){
fun(n/2);//向下划分为子问题
// 第一个双重循环完成第二个矩阵
for(i=0;i<n/2;i++)
for(j=n/2;j<n;j++)
matrix[i][j]=matrix[i][j-n/2]+n/2;
// 第二个双重循环完成第三个矩阵
for(i=n/2;i<n;i++)
for(j=0;j<n/2;j++)
matrix[i][j]=matrix[i-n/2][j+n/2];
// 第二个双重循环完成第四个矩阵
for(i=n/2;i<n;i++)
for(j=n/2;j<n;j++)
matrix[i][j]=matrix[i-n/2][j-n/2];
}
// 完成第一个2 ×2矩阵
else{
matrix[0][0] = 1;matrix[0][1]=2;
matrix[1][0] = 2;matrix[1][1]=1;
}
}
