类似的，我们的盘古自研框架BackPropagation也是同样的Back Propagation误差计算过程，actual_value是instances最后一列的实际值，predicted_value是预测值，预测值和真实值之间的误差值是minor_error（类似图中的δ）。如果我们的隐藏层设置为hidden_layers= [8,4,2]，首先计算输出层节点的误差值minor_error，然后从后往前循环遍历神经网络的神经元节点（输入层的X1，X2除外），例如：计算第三层隐藏层第二个神经元节点N[3][2]节点的误差，其误差值为affecting_theta *affected_minor_error，即N[3][2]节点与输出节点的连接权重乘以输出节点的误差值minor_error；又如计算第二层隐藏层的第一个神经元节点N[2][1]节点的误差值，先计算出N[3][1]节点的误差乘以N[2][1]与N[3][1]之间的连接权重，再计算出N[3][2]节点的误差乘以N[2][1]与N[3][2]之间的连接权重，然后将两者相加计算出N[2][1]节点的误差值。

•  
•  
•  
•  
•  
•  
•  
•  

Hidden layer creation: 1       N[1][1]         N[1][2]         N[1][3]         N[1][4]         N[1][5]         N[1][6]         N[1][7]         N[1][8]         Hidden layer creation: 2        N[2][1]         N[2][2]         N[2][3]         N[2][4]         Hidden layer creation: 3        N[3][1]         N[3][2]  

                           

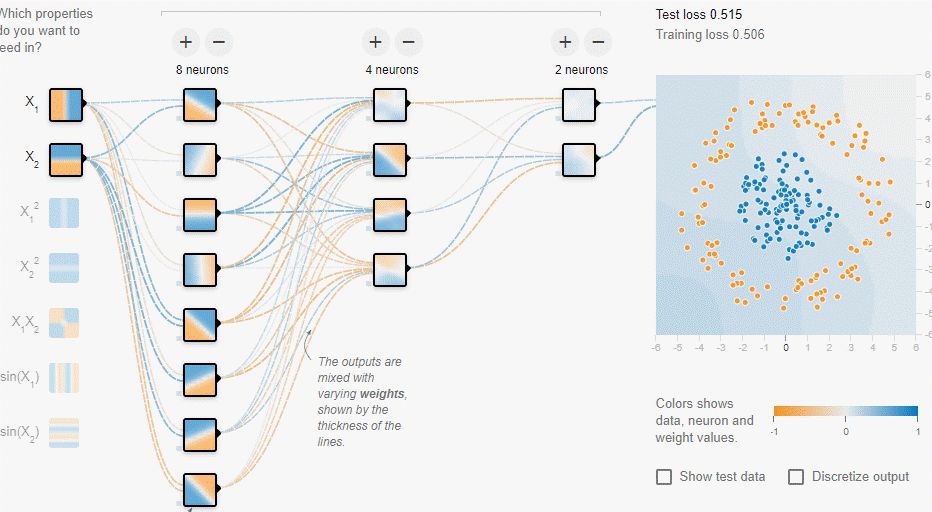
图 1- 40误差计算说明

这样在循环遍历的时候计算每个神经元Neuron（输入层的X1，X2除外）对误差结果应该负的责任。

• 最关键的地方是运行梯度下降算法进行求导调整权重。因为我们在

ForwardPropagation使用的是SigmoidActivation，所以这里是对Sigmoid进行求导。 导数的变化率根据梯度或误差进行计算，梯度根据链式推导从后往前推，要减少梯度或误差。最后得出的结果误差是输入数据和最后神经元的值导致的，最后神经元的值是根据前面神经元的值乘以权重导致的，而前面神经元的值又是根据上一层神经元的值乘以权重导致的，而上一层神经元的值又是根据输入层的值乘以权重导致的，而输入的值是训练数据集，输入数据的值不变的。因此，到底是什么导致误差，是权重的分配导致了误差！构建神经元网络的时候，初始化权重为（-1，1），根据输入的数据得出最后的结果，误差最终的原因是由于权重导致的！从计算过程角度，导致误差是因为权重不太对，权重需要调整！

Create_AI_Framework_In5Classes(Day3)版本的BackPropagation.py梯度下降代码：

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

class BackPropagation: …..  for j in range(len(weights)):                weight_from_node_value = 0                weight_to_node_value = 0                weight_to_node_error = 0                                for k in range(len(nodes)):                                        if nodes[k].get_index() == weights[j].get_from_index():                        weight_from_node_value = nodes[k].get_value()                                        if nodes[k].get_index() == weights[k].get_to_index():                        weight_to_node_value == nodes[k].get_value()                        weight_to_node_error = nodes[k].get_minor_error()                                                        #进行求导，因为我们在ForwardPropagation使用的是Sigmoid Activation，所以这里是对Sigmoid进行求导                # Forward Propagation中的Sigmoid代码：target_neuron_output = 1 / (1 + math.exp(- target_neuron_input))                                derivative = weight_to_node_error * (weight_to_node_value * (1 - weight_to_node_value                                                                             )) * weight_from_node_value                                #更新Weight，这是下次计算的时候能够更加准确的关键，因为把上面的计算成果运用在了调整Neuron Network的Weights上                                                                            weights[j].set_value(weights[j].get_value() - derivative * learning_rate)                  return nodes, weights         ……..

计算出神经元各节点的误差以后，接下来在Back Propagation中应用梯度下降算法进行求导，更新调整权重，其实现的原理机制如图所示，计算每个神经元的损失信号的时候，每个神经元的输入节点权重系数被修改。公式df(e)/de代表每个神经元激活函数的梯度。 

                           

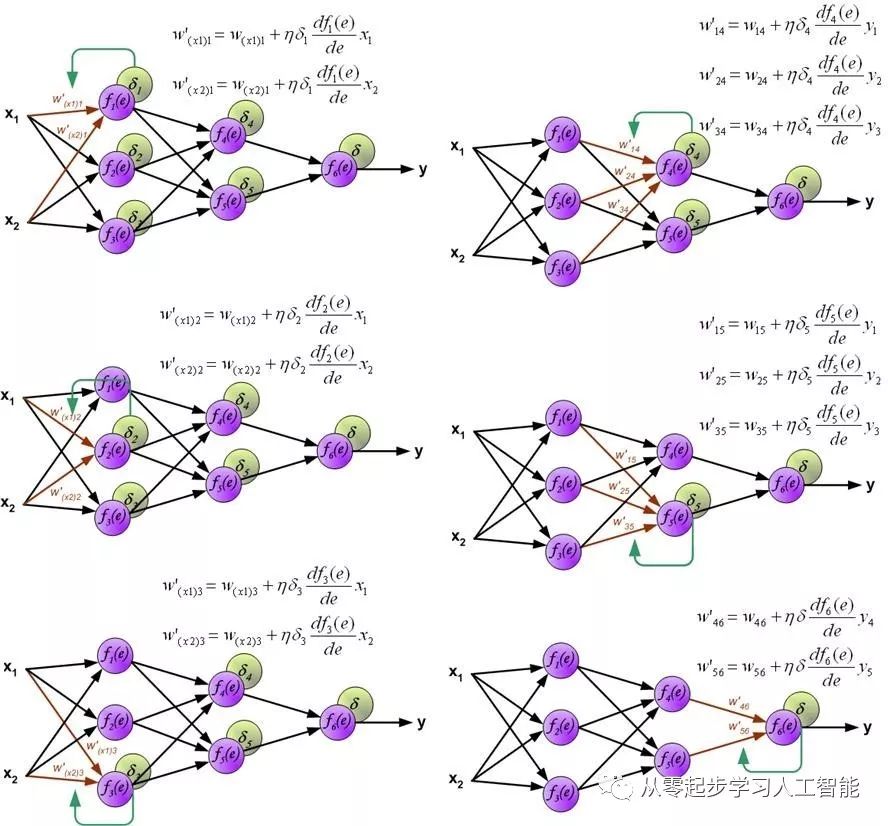
图 1- 41梯度求导

类似的，我们的盘古自研框架BackPropagation也是同样的Back Propagation梯度下降算法求导计算过程。