一、算法原理
滑动窗口,顾名思义,就是有一个大小可变的窗口,左右两端方向一致的向前滑动(右端固定,左端滑动;左端固定,右端滑动)。

滑动窗口的本质其实也是一种双指针算法,它是根据单调性的思想,使用”同向双指针“,索引字符串或者列表中的一个区间[left,right]。
滑动窗口的步骤一般如下所示:
1、在序列中使用双指针中的左右指针技巧,初始化
left = right = 0,把索引闭区间[left, right]称为一个窗口。
2、先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的序列符合要求。
3、此时,停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的序列不再符合要求。同时,每次增加 left前,都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达序列的尽头。
二、算法实战
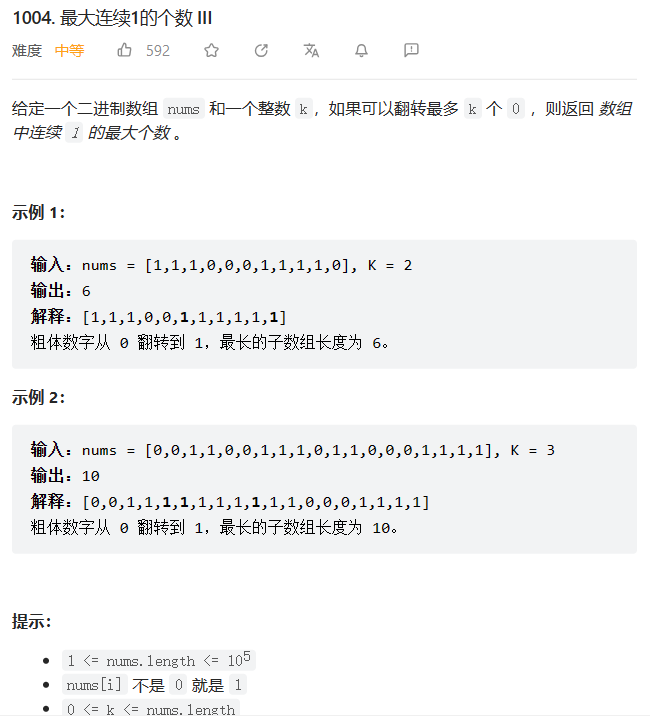
1. leetcode209 长度最小的子数组
长度最小的子数组
解题思路:

代码实现:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int left = 0, right = left, n = nums.size() - 1;
int Min = 0, sum = 0;
while(right <= n)
{
sum += nums[right];
while(sum >= target)
{
int tmp = right - left + 1;
Min = Min == 0 ? tmp : min(tmp, Min);
sum -= nums[left++];
}
right++;
}
return Min;
}
};
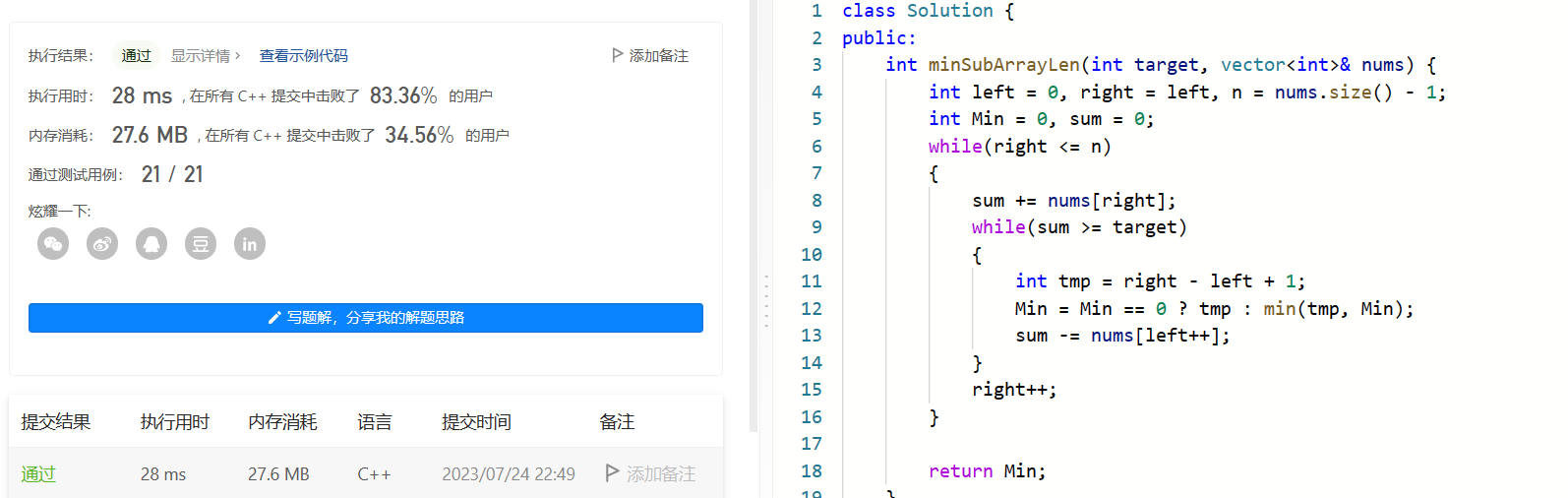
2. leetcode3 无重复字符的最长子串
无重复字符的最长字串
解题思路:滑动窗口+哈希表
题目要求的是无重复字符,为了统计每个字符出现的次数,这里我们可以使用哈希表来统计每个字符出现的次数。

代码实现:
class Solution {
public:
//滑动窗口问题
int lengthOfLongestSubstring(string s) {
int hash[128] = {0};
int n = s.size() - 1, len = 0;
for(int left = 0, right = 0; right <= n; right++)
{
hash[s[right]]++; // 进窗口
while(hash[s[right]] > 1)
{
hash[s[left]]--;//不满足要求,出窗口,直到满足要求为止
left++;
}
len = max(len, right - left + 1);
}
return len;
}
};
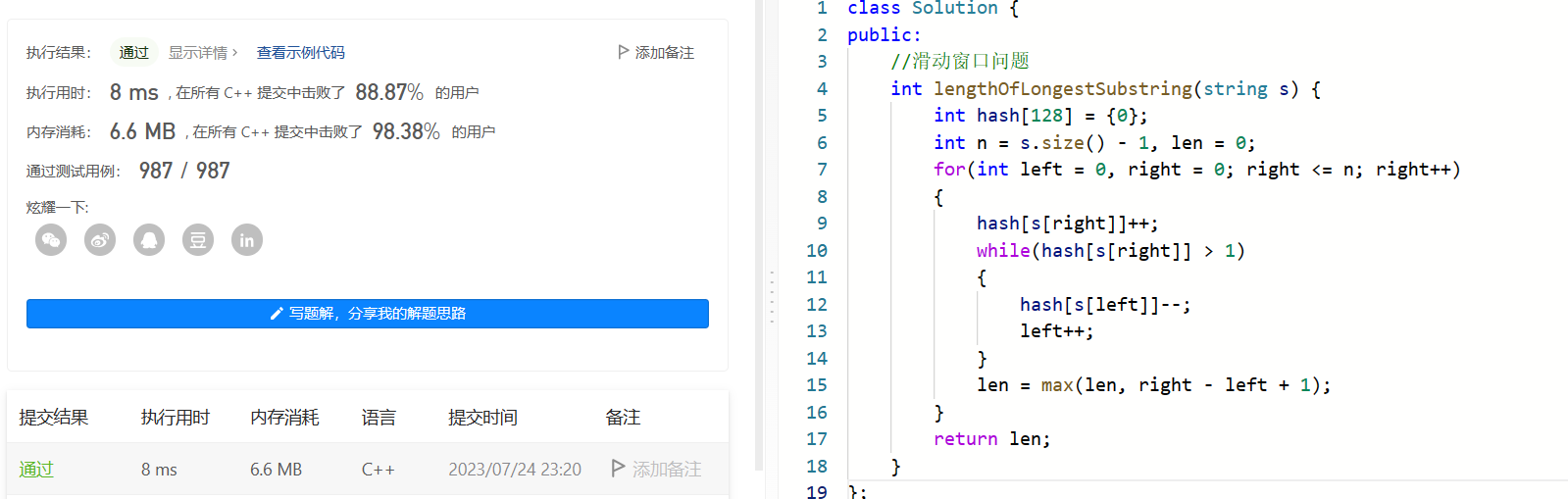
3. leetcode1004 最大连续1的个数
最大连续1的个数III
解题思路:
因为数组中除了0就是1,题目要求我们最多只能翻转k个0,求的是翻转k个0后,最长连续1的个数。
我们可以转换一下思路:找出最长的子数组,该子数组中0的个数不超过k个。

代码实现:
class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
int n = nums.size();
int zero = 0, ret = 0;
for(int left = 0, right = 0; right < n; right++)
{
if(nums[right] == 0)
zero++;
while(zero > k)
{
if(nums[left] == 0)
zero--;
left++;
}
ret = max(ret, right - left + 1);
}
return ret;
}
};
4. leetcode1685 将x减到0的最小操作数
将x减到0的最小操作数
这个题目我们可以进行进一步转化:转换为——> 找出最长的子数组的的长度,所有元素的和正好等于 sum-x,然后再利用滑动窗口解决即可。
代码实现:
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
int n = nums.size();
int sum = 0, target = 0;
for(int i = 0; i < n; i++)
sum += nums[i];
target = sum - x, sum = 0;
int len = -1;
if(target < 0) return -1;
for(int left = 0, right = 0; right < n; right++)
{
sum += nums[right]; // 进窗口
while(sum > target) // 判断
{
sum -= nums[left++]; // 出窗口
}
if(sum == target) // 更新结果
len = max(len, right - left + 1);
}
return len == -1 ? len : n - len;
}
};
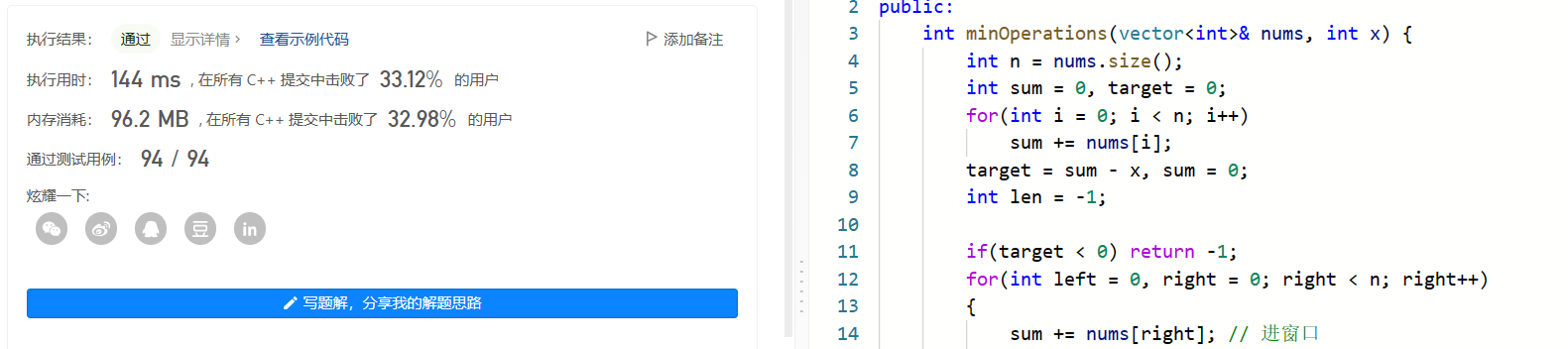
5. leetcode904 水果成篮
水果成篮
这道题目的解法是利用滑动窗口+哈希表,数组中的元素表示水果种类的编号,我们只需要利用滑动窗口来进行解决,找到在篮子中的水果种类不超过2的情况下,求出窗口最长的情况即可。
代码实现:
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int n = fruits.size(), hash[100010] = {0}, kinds = 0, len = 0;
for(int left = 0, right = 0; right < n; right++)
{
if(++hash[fruits[right]] == 1) // 进窗口
kinds++;
while(kinds > 2) // 判断
{
if(--hash[fruits[left++]] == 0) // 出窗口
kinds--;
}
if(kinds <= 2) // 更新结果
len = max(len, right - left + 1);
}
return len;
}
};
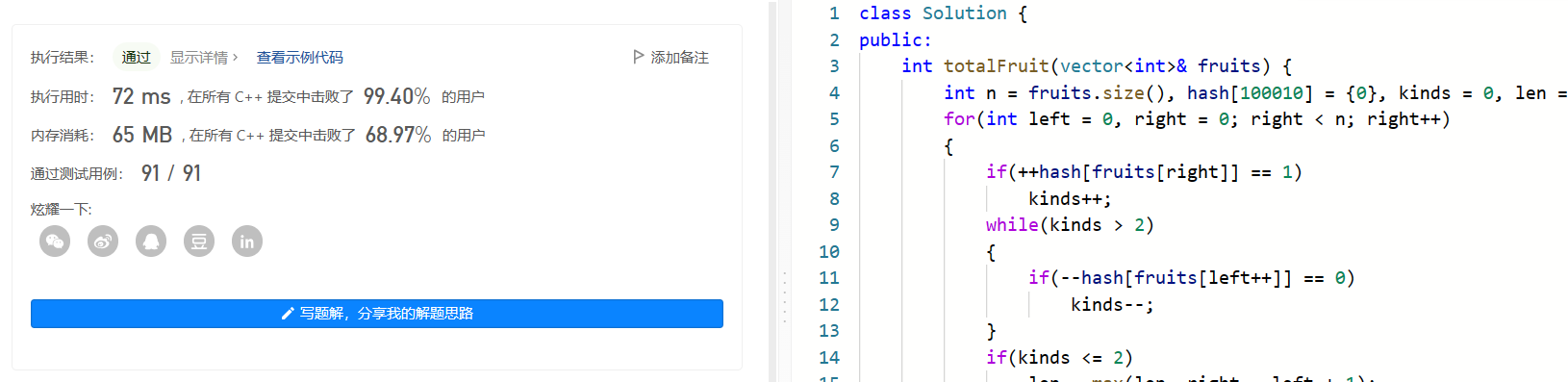
6. leetcode438 找到字符串中所有字母异位词
找到字符串中所有字母异位词
这道题目依旧是利用滑动窗口+哈希表,我们可以先统计目标单词中出现的次数,将其映射到哈希表。维护一个判断窗口中有效字符的个数的变量cnt,从左向右依次利用滑动窗口遍历即可,这里因为单词的长度是固定的,因此每进一个窗口、如过窗口长度大于单词的长度,就必须让最左边的元素出窗口。
代码实现:
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> ret;
int hash1[26] = {0}, hash2[26] = {0}, len = p.size();
for(auto&e : p)
hash2[e - 'a']++;
int cnt = 0;//判断窗口中的有效字符
for(int left = 0, right = 0; right < s.size(); right++)
{
if(++hash1[s[right] - 'a'] <= hash2[s[right] - 'a']) //进窗口
cnt++;
if(right - left + 1 > len) // 判断
{
if(--hash1[s[left] - 'a'] < hash2[s[left] - 'a']) //出窗口
cnt--;
left++;
}
//判断结构是否合法
if(cnt == len) // 更新结果
ret.emplace_back(left);
}
return ret;
}
};
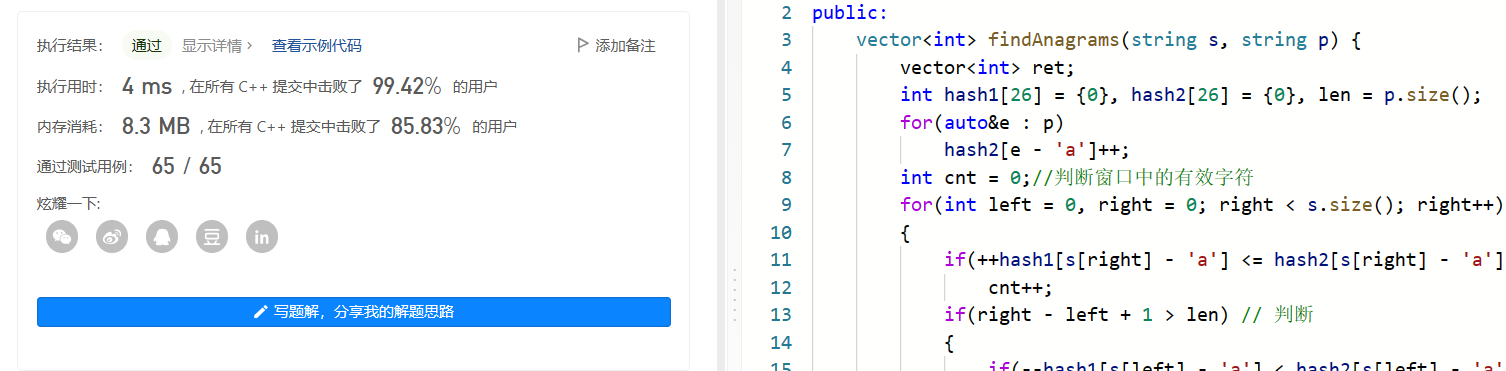
7. leetcode30 串联所有单词的子串
串联所有单词的子串
这道题目和上一道题目很相似,无非就是上一道题目解决的是字符,这道题目解决的是字符串。依然使用的方法是滑动窗口+哈希表,因为这里提前告诉我了我们——目标字符串数组中的每个单词的长度都相同。所以根据这个条件我们可以大大降低时间复杂度。
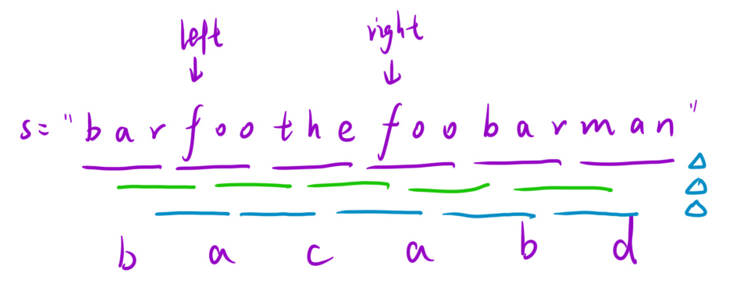
这里我们需要注意的是,滑动窗口在出入窗口的过程中,移动的步长是单词的长度,滑动窗口执行的次数是单词的长度次。
代码实现:
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
unordered_map<string,int> hash2;//开两个哈希表
for(auto& e : words)
hash2[e]++;
vector<int> ret;
ret.reserve(s.size());
int len = words.size(), cnt = 0, n = words[0].size();
for(int i = 0; i < n; i++) // 执行n次
{
unordered_map<string,int> hash1; // 维护窗口内单词的频次
cnt = 0;
for(int left = i, right = i + n; right <= s.size(); right += n)
{
string tmp = s.substr(right - n, n);
if(hash2.count(tmp) && ++hash1[tmp] <= hash2[tmp])
cnt++;
if(right - left > n*len) // 出窗口,维护cnt
{
string tmp = s.substr(left, n);
if(hash2.count(tmp) && --hash1[tmp] < hash2[tmp])
cnt--;
left += n;
}
if(cnt == len) // 更新结果
ret.emplace_back(left);
}
}
return ret;
}
};
8. leetcode76 最小覆盖子串
最小覆盖子串
这里给出我们的目标字符串t中的字符种类可能是重复出现的。和上面的题目”找到字符串中所有字母异位词“有所不同:这里我们进窗口时的判断条件应该是:当窗口中出现的字符个数等于目标串某个字符的个数时,变量cnt++,这样保证最后入窗口的字符个数等于目标字符串中指定字符个数时,也就是更新条件成立时,窗口中字符的种类 == 目标字符串,窗口中的字符个数一定是 >= 目标字符串的字符的。保证了窗口中的字符串一定是能够完全覆盖目标字符串。最后在满足判断更新条件的循环中不断出窗口,直到出到不能在出为止。
代码实现:
class Solution {
public:
string minWindow(string s, string t) {
int hash1[128] = {0}, hash2[128] = {0}, kinds = 0;
for(auto ch : t)
if(hash2[ch]++ == 0) kinds++;
int cnt = 0, Min = INT_MAX, begin = -1;
for(int left = 0, right = 0; right < s.size(); right++)
{
if(++hash1[s[right]] == hash2[s[right]])
cnt++;
while(cnt == kinds)
{
if(right - left + 1 < Min)
Min = right - left + 1, begin = left;
char out = s[left++];
if(hash1[out]-- == hash2[out])
cnt--;
}
}
if(begin == -1) return "";
else return s.substr(begin, Min);
}
};
三、总结
滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。 该技术可以将一部分问题中的嵌套循环转变为一个单循环,因此它可以减少时间复杂度。 简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。