题目
假设二叉树采用二叉链表存储结构存储,设计一个算法求出二叉树的宽度(具有结点数最多的那一层上的结点个数)。
分析
要求含有最多结点数的层上的结点数,可以分别求出每层的结点数,然后从中选出最多的。 要达到这个目的,应该明白两个事实。
第一,对于非空树,树根所在的层为第一层,并且从层次遍历算法的程序中可以发现,有-个由当前结点找到其左、右孩子结点的操作。这就提示我们,如果知道当前结点的层号,就可以推出其左、右孩子的层号,即为当前结点层号加1,进而可以求出所有结点的层号。
第二,在层次遍历中,用到了一个循环队列(队列用数组表示),其出队和入队操作为front=(front+ 1)%maxSize;和rear=(rear+1)%maxSize;两句。如果用来存储队列的数组足够长,可以容纳树中所有结点,这时在整个遍历操作中队头和队尾指针不会出现折回数组起始位置的情况,那么front=(front+ 1)%maxSize;可以用++front;代替,rear=(rear+1)%maxSize; 可以用++rear:代替。出队操作只是队头指针front后移了一一位,但并没有把队头元素删除。在数组足够长的情况下,队头元素也不会被新入队的元素覆盖。
代码
核心代码:
/* 求二叉树的宽度 */
int maxNode(BTNode *b) {
St que[maxSize];
int front,rear;// 定义顺序非循环队列
int Lno=0,i,j,n,max=0;
front=rear=0;// 将队列置空
BTNode *q;
if(b!=NULL) {
rear++;
que[rear].p=b;// 树根入队
que[rear].lno=1;// 树根所在的层次号设置为1,此为已知条件
while(front!=rear) {
front++;
q=que[front].p;
Lno=que[front].lno;// 关键语句:Lno用来存取当前结点的层次号
if(q->lchild!=NULL) {
rear++;
que[rear].p=q->lchild;
que[rear].lno=Lno+1;// 关键语句:根据当前结点的层次号,推知其孩子结点的层次号
}
if(q->rchild!=NULL) {
rear++;
que[rear].p=q->rchild;
que[rear].lno=Lno+1;// 关键语句:根据当前结点的层次号推知其孩子结点的层次号
}
} // 注意:循环结束的时候,Lno中保存的是这颗二叉树的最大层数
/* 以下代码找出了含有结点最多的层中的结点数 */
max=0;
for(int i=1; i<=Lno; i++) {
n=0;
for(j=0; j<rear; j++) {
if(que[j].lno==i) {
n++;
}
if(max<n) {
max=n;
}
}
}
return max;
} else {
return 0;// 空树直接返回0
}
}完整代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#define maxSize 30
/* 数结构体类型定义*/
typedef struct BTNode {
char data;// 这里默认结点data域为char类型
struct BTNode *lchild;// 左孩子指针域
struct BTNode *rchild;// 右孩子指针域
} BTNode,*BiTree;
/* 该结构体为顺序非循环队列的队列的队列元素,可以存储结点指针以及结点所在的层次号 */
typedef struct {
BTNode *p;// 结点指针
int lno;// 结点所在的层次号
} St;
/* 根据输入创建二叉树 */
/* 例:ABC##DE##F##GH### */
void CreatBiNode(BTNode **Node) { //此处应注意传递的参数(二重指针)
char data;
scanf("%c", &data);
*Node = (BiTree)malloc(sizeof(BTNode));
if (data == '#') {
*Node = NULL;
} else if ((data != '#') && (*Node)) {
(*Node)->data = data;
(*Node)->lchild = NULL;
(*Node)->rchild = NULL;
CreatBiNode(&(*Node)->lchild);
CreatBiNode(&(*Node)->rchild);
}
}
/* 求二叉树的宽度 */
int maxNode(BTNode *b) {
St que[maxSize];
int front,rear;// 定义顺序非循环队列
int Lno=0,i,j,n,max=0;
front=rear=0;// 将队列置空
BTNode *q;
if(b!=NULL) {
rear++;
que[rear].p=b;// 树根入队
que[rear].lno=1;// 树根所在的层次号设置为1,此为已知条件
while(front!=rear) {
front++;
q=que[front].p;
Lno=que[front].lno;// 关键语句:Lno用来存取当前结点的层次号
if(q->lchild!=NULL) {
rear++;
que[rear].p=q->lchild;
que[rear].lno=Lno+1;// 关键语句:根据当前结点的层次号,推知其孩子结点的层次号
}
if(q->rchild!=NULL) {
rear++;
que[rear].p=q->rchild;
que[rear].lno=Lno+1;// 关键语句:根据当前结点的层次号推知其孩子结点的层次号
}
} // 注意:循环结束的时候,Lno中保存的是这颗二叉树的最大层数
/* 以下代码找出了含有结点最多的层中的结点数 */
max=0;
for(int i=1; i<=Lno; i++) {
n=0;
for(j=0; j<rear; j++) {
if(que[j].lno==i) {
n++;
}
if(max<n) {
max=n;
}
}
}
return max;
} else {
return 0;// 空树直接返回0
}
}
int main() {
printf("先序输入二叉树(空结点用'#'表示):");
BiTree T=NULL;
CreatBiNode(&T);// 创建二叉树
/* 求二叉树的宽度 */
int r=maxNode(T);
printf("二叉树的宽度:%d",r);
return 0;
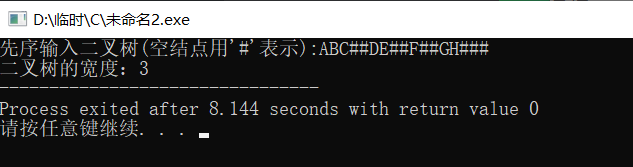
}以下图为例输入(其中空结点用“#”表示),输入的字符串如下:

运行结果: