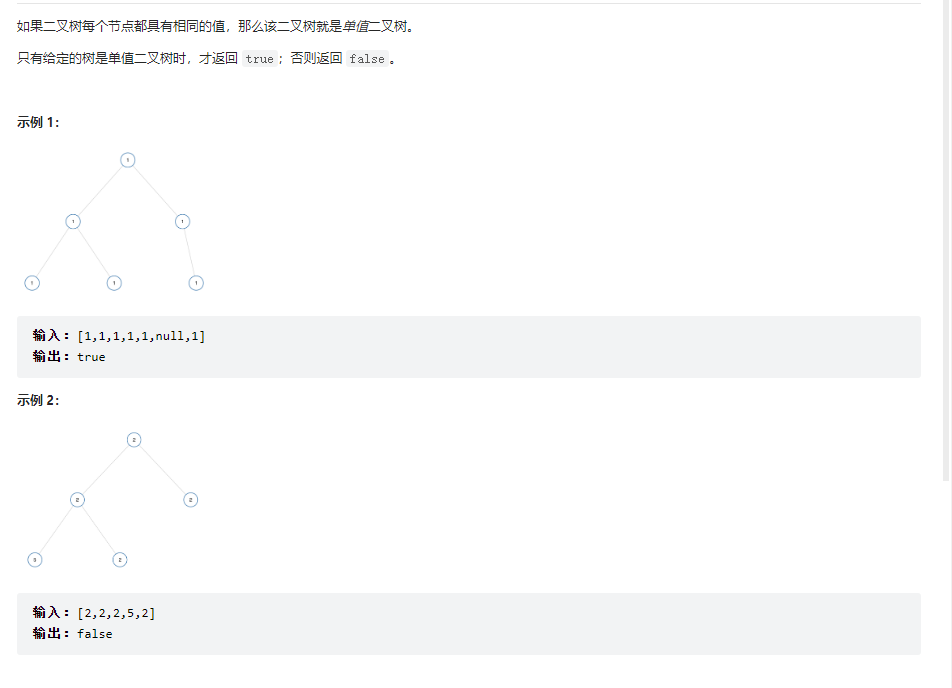
单值二叉树

简单来说，结点的值都要相同。那我们可以去判断当前结点的值和左孩子的值相不相同，再去判断当前结点的值和右孩子的值相不相同。只要出现不同，那我们直接返回错误。再去递归左右孩子，直到结束。

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
    {
        return true;
    }
    else if(root->left!=NULL&&root->val != (root->left)->val)
    {
        return false;
    }
    else if(root->right!=NULL&&root->val!=(root->right)->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

这里有一个比较容易错的地方：判断的时候除了要判断结点的值是否相等之外，左右孩子必须是存在的！

相同的树

两棵树分别去比较（都为空肯定相等，其中一个为空就不相等），根的值比较，对应的子树比较。还是采用递归解决

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

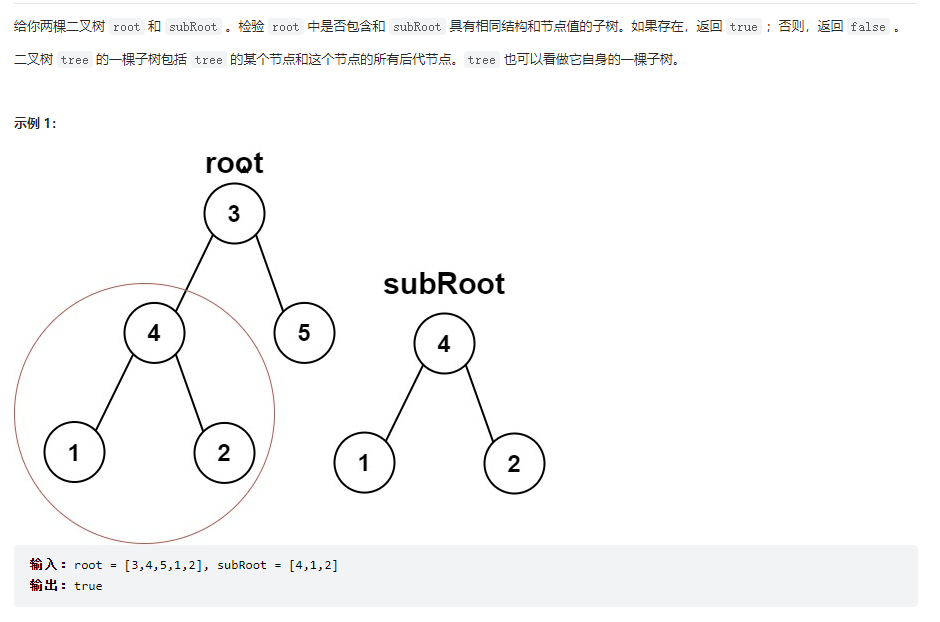
另一棵树的子树

这是一个很有意思的题目，我们可以让原树中的每颗子树(包括原树)去和subRoot比较。怎么比较❓我们可以利用上面的题相同的树去的函数进行判断。让原树的每个子树去比较即可

bool isSametree(struct TreeNode*p,struct TreeNode*q)
{
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSametree(p->left,q->left)&&isSametree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root==NULL)
    {
        return false;
    }
    if(isSametree(root,subRoot))
    {
        return true;
    }
    return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

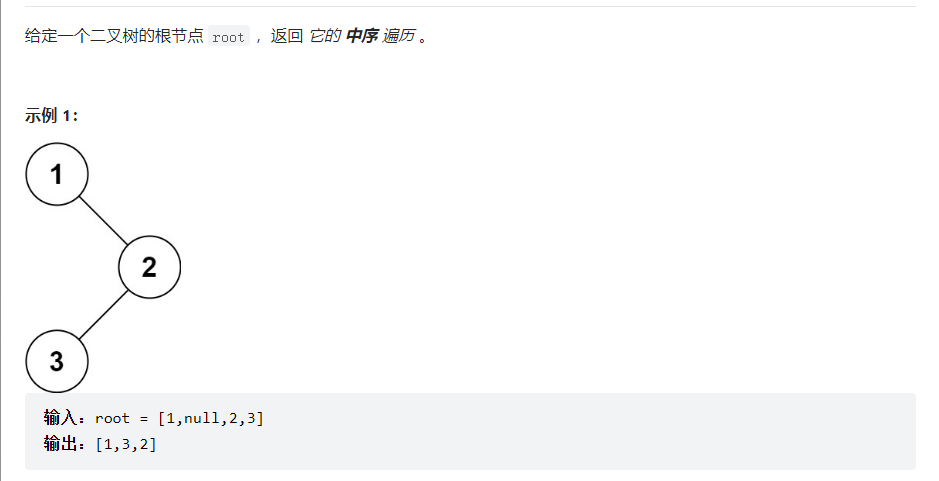
二叉树的前序遍历

这道题可不是简单的打印出前序遍历。我们需要把结果存放在开辟的数组中。我们可以通过算出结点的个数开辟对应的空间。再根据前序遍历把结果放到数组中：

int TreeSize(struct TreeNode*root)
 {
     if(root==NULL)
     {
         return 0;
     }
     return TreeSize(root->left)+TreeSize(root->right)+1;
 }
 void PreOrder(struct TreeNode*root,int*a,int*pi)
 {
     if(root == NULL)
     {
         return;
     }
     a[*pi] = root->val;
     (*pi)++;
     PreOrder(root->left,a,pi);
     PreOrder(root->right,a,pi);
            
 }
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int n = TreeSize(root);
    int*arr = (int*)malloc(sizeof(int)*n);
    int i = 0;
    PreOrder(root,arr,&i);
     *returnSize = n;
    return arr;
}

趁热打铁

二叉树的中序遍历

一样的做法：

 int TreeSize(struct TreeNode*root)
 {
     if(root==NULL)
     {
         return 0;
     }
     return TreeSize(root->left)+TreeSize(root->right)+1;
 }

 void InOrder(int*arr,struct TreeNode*root,int*pi)
 {
     if(root==NULL)
     {
         return;
     }
    InOrder(arr,root->left,pi);
     arr[*pi] = root->val;
     (*pi)++;
     InOrder(arr,root->right,pi);
 }

int* inorderTraversal(struct TreeNode* root, int* returnSize){
    int n = TreeSize(root);
    int*arr = (int*)malloc(sizeof(int)*n);
    int i = 0;
    InOrder(arr,root,&i);
    *returnSize = n;
    return arr;
}

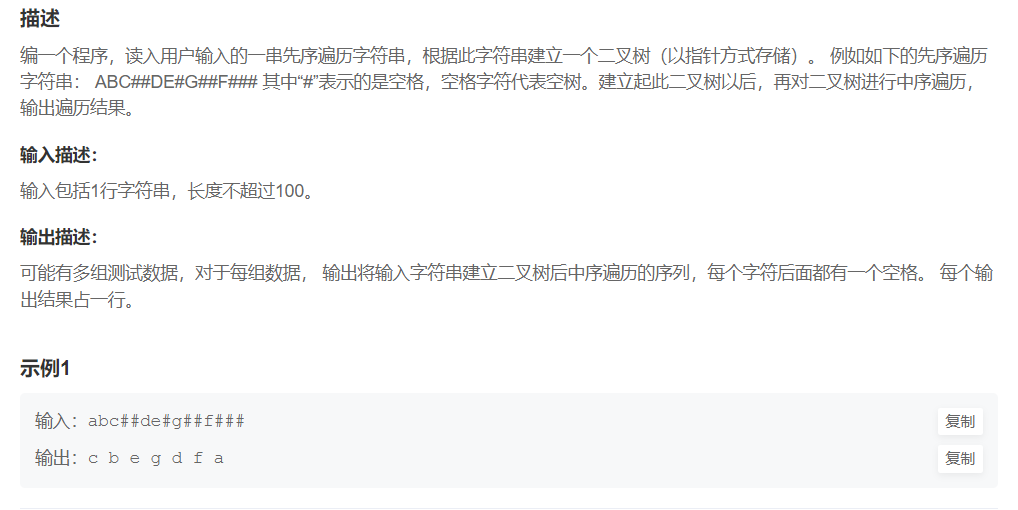
二叉树遍历

题目要求很简单：给出前序遍历，让我们建立二叉树，最后进行中序遍历输出。

我们得先了解怎么去建立，我们以上面的示例1为例子：

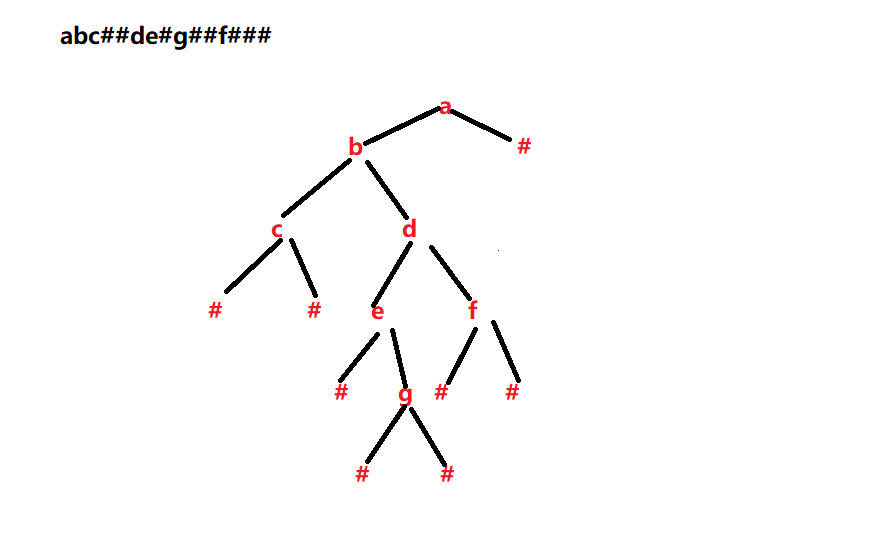
代码实现：

#include <stdio.h>
#include <stdlib.h>

typedef char BTDataType;
typedef struct BinarryTree
{
    struct BinarryTree*left;
    struct BinarryTree*right;
    BTDataType data;
}BTNode;

BTNode* BinarryTreeCreate(BTDataType* str,int*pi)
{
    if(str[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    BTNode*root = (BTNode*)malloc(sizeof(BTNode));
    if(NULL == root)
    {
        perror("malloc fail");
        exit(-1);
    }
    root->data = str[*pi];
    (*pi)++;
    root->left = BinarryTreeCreate(str,pi);
    root->right = BinarryTreeCreate(str,pi);
    return root;
}

void InOrder(BTNode*root)
{
    if(root==NULL)
        return;
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}

int main()
{
    char str[101];
    gets(str);
    int i = 0;
    BTNode*root = BinarryTreeCreate(str,&i);
    InOrder(root);
    return 0;
}

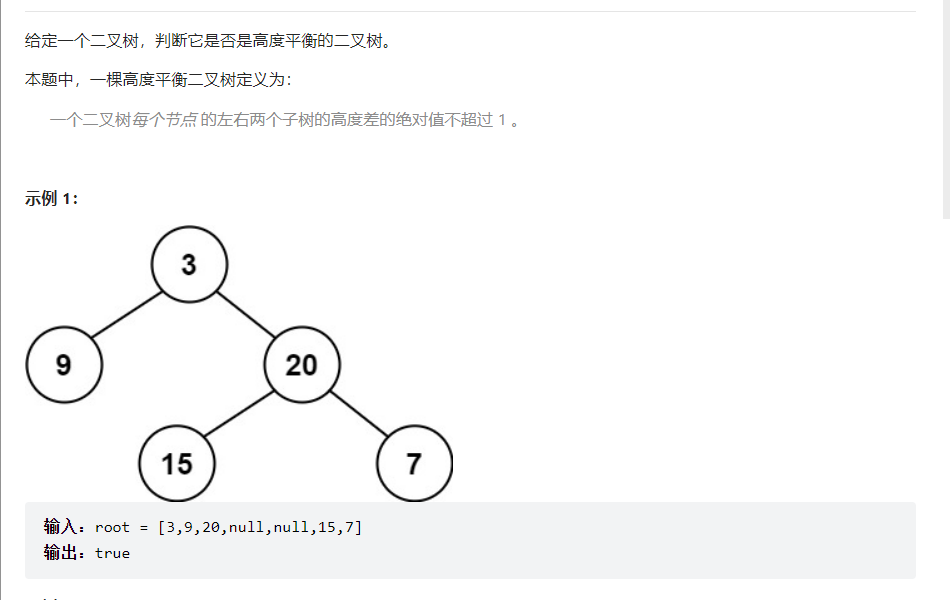
平衡二叉树

这道题我的思路是求出左子树的高度和右子树的高度，判断差值，大于1就直接返回false，然后再去递归左子树和右子树

int TreeDepth(struct TreeNode*root)
{
    if(root==NULL)
    {
        return 0;
    }
    int left = TreeDepth(root->left);
    int right = TreeDepth(root->right);
    return left>right?left+1:right+1;
}
bool isBalanced(struct TreeNode* root){
    if(root == NULL||(root->left==NULL)&&(root->right==NULL))
        return true;
    if(abs(TreeDepth(root->left)-TreeDepth(root->right))>1)
        return false;
    return isBalanced(root->left)&&isBalanced(root->right);
}

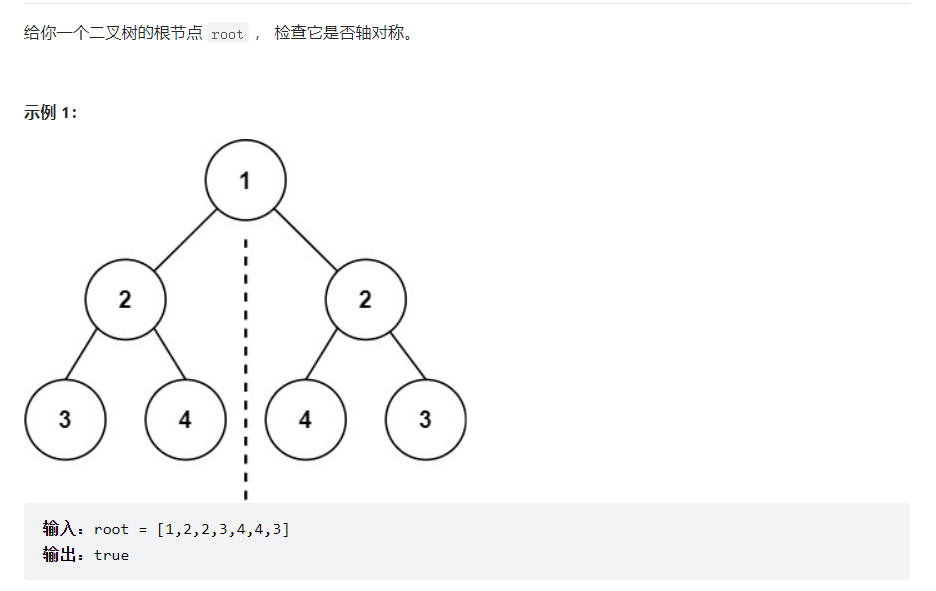
对称二叉树

如果是对称二叉树的话，那么左子树和右子树同时为空，左结点的左值会等于右结点的右值，左结点的右值会等于右结点的左值。我们可以采用递归的方式来完成这道题：

bool judge(struct TreeNode* left,struct TreeNode* right){
    if(left == NULL && right == NULL)
        return true;
    if(left == NULL || right == NULL || left -> val != right -> val)
        return false;
    return judge(left -> left,right -> right) && judge(left -> right,right -> left);
}

bool isSymmetric(struct TreeNode* root){
    if(root == NULL)
        return true;
    return judge(root -> left,root ->right);
}

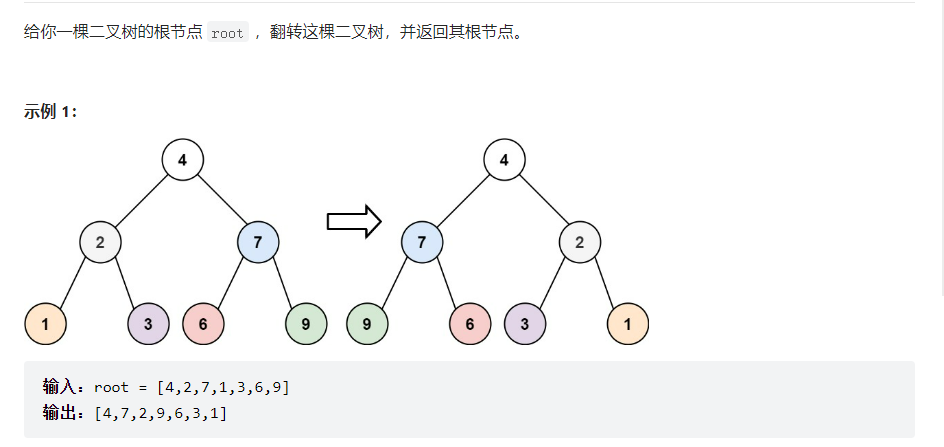
翻转二叉树

实际上就是左右子树进行交换即可：

struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL)
        return NULL;
    struct TreeNode*tmp = root->left;
    root->left = root->right;
    root->right = tmp;

    invertTree(root->left);
    invertTree(root->right);
    return root;
}

---

结语

通过这几道简单的题目，我们对于递归有了进一步的理解，同时加深了对二叉树的理解，如果觉得自己学有余力的情况之下，我们还可以去做更多的题目，当然，这里的二叉树知识是比较基础的，后面会更进一步的学习，这次就先到这里结束了。