核心考点:数组理解,二分查找,临界条件
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}是数组{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。NOTE:给出的所以元素都大于0,若数组大小为0,请返回0。
解析一:(不提倡)
寻找数组当中的最小值,不管怎么说,遍历一遍数组当中元素是肯定能找到的。
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.size() == 0) //数组大小为0,返回0
return 0;
int min = rotateArray[0];
//遍历数组寻找最小值
for (size_t i = 1; i < rotateArray.size(); i++)
{
if (rotateArray[i] < min)
min = rotateArray[i];
}
return min; //返回最小值
}
};
解析二:(较提倡)
因为原数组是一个非递减的数组,所以原数组当中的每一个元素都大于或等于其前面的一个元素,而原数组经过旋转后被分为两部分(一部分是被旋转到后面的,另一部分是未被旋转的),这两部分也分别满足该规律(每一个元素都大于或等于其前面一个元素)。

所以我们可以挨个比较数组当中相邻的两个元素,若前一个元素小于或等于后一个元素,则继续比较;若前一个元素大于后一个元素,则说明这两个元素之间就是分界处,此时返回后一个元素即可。
若是遍历完数组都没有找到前一个元素大于后一个元素的情况,则说明旋转数组是由原数组的全部元素旋转后得到的(旋转后的数组与原数组相同),此时返回数组的第一个元素即为最小值。
该解法找到特定情况后便可以直接返回数组当中的最小值,相对于第一种解法来说效率会高一点,但其查找效率的快慢却决于数组的旋转深度。
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.size() == 0) //数组大小为0,返回0
return 0;
for (size_t i = 1; i < rotateArray.size(); i++)
{
if (rotateArray[i - 1] > rotateArray[i]) //找到前一个元素小于后一个元素的情况
return rotateArray[i]; //返回后者即为最小值
}
return rotateArray[0]; //数组遍历结束,返回数组的第一个元素即为最小值
}
};
解析三:(正解)
对于该题目,我们还可以使用二分查找的方式:找到数组的中间元素mid,将mid与某一元素进行比较,确定最小值位于mid的哪一侧,从而达到查找一次后待查找元素减半的效果。
这里我们选择将中间元素mid与数组的最后一个元素进行比较(也可以选择将其与第一个元素进行比较),那么会出现以下四种情况:
情况一: left索引的元素小于right索引的元素。
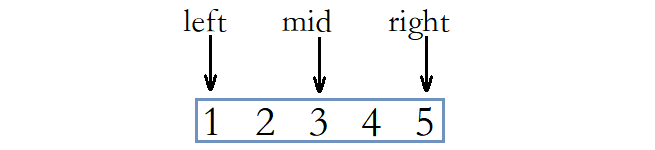
此时说明[left, right]区间内的元素已经是非递减序列了,left索引的元素便是数组当中的最小值。
情况二: mid索引的元素小于right索引的元素。
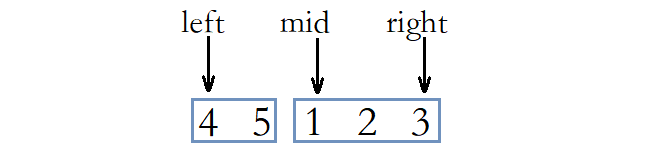
此时说明[mid+1, right]区间内的元素都大于等于mid索引的元素,而mid左侧还有可能有比mid索引的元素更小的元素,所以将待查找区间缩小为[left, mid]。
情况三: mid索引的元素大于right索引的元素。
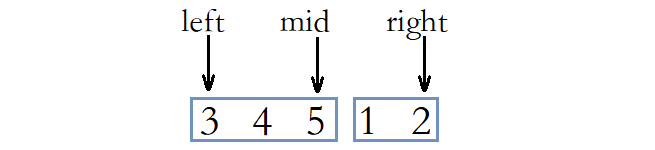
此时说明[left, mid]区间内的元素都大于等于right索引的元素,而在mid和right之间可能有比right索引的元素更小的元素,所以将待查找区间缩小为[mid+1, right]。
情况四: mid索引的元素等于right索引的元素。
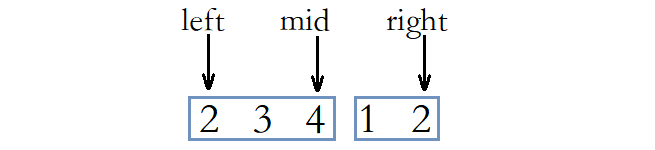
此时无法判断数组最小值位于mid的哪一侧,我们可以选择将right左移一个位置,然后重新进行判断。
通过这种方法一直判断下去,直到出现第一种情况得到最小值,或是直到left和right所确定的区间当中只有一个元素时,这一个元素便是数组当中的最小值。
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.size() == 0) //数组大小为0,返回0
return 0;
int left = 0, right = rotateArray.size() - 1;
while (left < right)
{
if (rotateArray[left] < rotateArray[right]) //[left,right]区间已经是非递减序列,返回区间内第一个元素即可
return rotateArray[left];
int mid = left + (right - left) / 2;
if (rotateArray[mid] < rotateArray[right]) //待查找区间缩小为[left, mid]
{
right = mid;
}
else if (rotateArray[mid] > rotateArray[right]) //待查找区间缩小为[mid+1, right]
{
left = mid + 1;
}
else //mid和right索引的元素值相同,将right往左移
{
right--;
}
}
return rotateArray[left]; //left和right所确定的区间当中只有一个元素,返回这个元素即可
}
};

