编写一个函数，输入是一个无符号整数（以二进制的形式），返回其二进制表达式中数字位数为‘1’的个数（也被称为汉明重量）。

示例：
 输入：n = 11
 输出：3

提示：
输入必须是长度为32的二进制串。

思路：
该题比较容易想到的一个方法是，循环32次，依次判断32个二进制位是否为1，最后返回1的个数即可。
但还有一个更简洁的方法：我们可以依次消去所给数字的32个二进制位中最右边的1，消去一个，计次就加一，直到二进制位当中没有1，此时的计次就是所给数字二进制中1的个数。
那么问题就变成了如何消去二进制中最右边的1，方法如下：
用所给数字n和n - 1进行按位与操作，操作后便可消去二进制中最右边的1。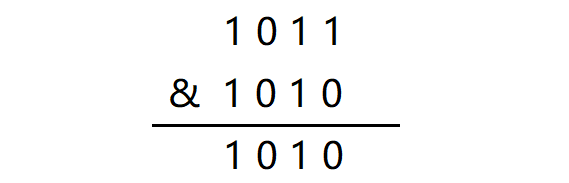

因为当数字减一后，二进制位当中最右边的1及其右边的二进制位都相当于进行了按位取反操作，而最右边的1的左边的二进制位保持不变，此时将其与原数字进行按位与操作，就相当于将二进制当中最右边的1消除了。

代码如下：

class Solution {
public:
	int hammingWeight(uint32_t n) {
		int count = 0; //统计二进制中1的个数
		while (n) //当n不等于0时，说明其二进制当中还有1存在
		{
			n = n&(n - 1); //消去二进制中最右边的1
			count++; //更新1的个数
		}
		return count; //返回二进制中1的个数
	}
};