1、概述
相比于 CPU,GPU 在架构设计时将更多的晶体管用于数据处理,而不是数据缓存和流量控制,因此可以高度实现并行计算。由于深度学习是基于大量矩阵运算实现的,因此我们往往使用 GPU 训练深度学习网络。GPU 的计算能力和显存大小决定了计算速度和可运行的网络的大小,但除了 GPU 本身的性能外,网络训练/推理的性能还与我们使用的数据类型有关。在大模型时代,低精度和混合精度的使用非常常见。本文列出NVIDIA CUDA支持的数据类型,详细分析每种数据类型的空间占用情况、数据表达能力和精度分辨。
2、基础概念
本节主要介绍数据的存储方式(包括高精度和低精度数据)
2.1 数据存储
浮点数据在计算机内都是以二进制方式存储的,主要由三部分组成:
- 符号位(Sign, 简称S): 0表示正数,1表示负数;
- 指数位(Exponent, 简称E): 用于存储科学计数法的指数部分,其大小决定了数据的表达能力(表示范围);
- 尾数位(Mantissa, 简称M): 用于存储尾数(小数)部分,其大小决定了数据能够表达的分辨率(精度);
2.2 高精度数据
下图展示了NVIDIA GPU中支持的高精度浮点数据类型, 详细给出了了每种数据类型的三部分分别占用的比特位数大小,后续我们根据每种数据类型对应部分的比特位数计算分析其表达能力和数值精度。
注意:
-
通常在科学计算领域只有double才算是高精浮点类型,在AI领域fp32也算是高精度表示了;
-
tf32数据只有10bit位表示小数(精度), 在AI领域也是低精度数据,这里为了跟fp32比较,将它画在一起;
2.3 低精度数据
下图展示了NVIDIA GPU中支持的低精度浮点数据类型, 详细给出了了每种数据类型的三部分分别占用的比特位数大小,后续我们根据每种数据类型对应部分的比特位数计算分析其表达能力和数值精度。特别强调是的,FP8格式有不同的表达,如E5M2/E4M3分别表示5bit指数+2bit精度的高表达低精度的类型,以及4bit指数+3bit小数的低表达高精度的类型(在NVIDIA GPU中,目前只有H100+的GPU才支持FP8精度!)。
3、能力与精度
为了彻底搞懂每一种数据类型的表达能力和精度,我们对2个典型的数据类型进行计算和分析,彻底搞懂特定数据表达能力和精度的计算方式和流程。
3.1 浮点数表示
我们首先回顾一下浮点数的表示方式
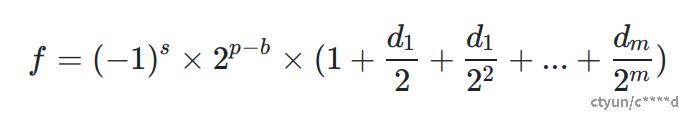
其中,

浮点数可以看做是在2^n和2^(n+1)两个连续2次幂至之间有m个均匀的网络,由于对于不同的数据范围,2^n到2^(n+1)之间的数值的数量不均等,因此浮点数在不同的范围内的精度也不相同。以为bf16例,其在不同数值区间的数值精度如下:
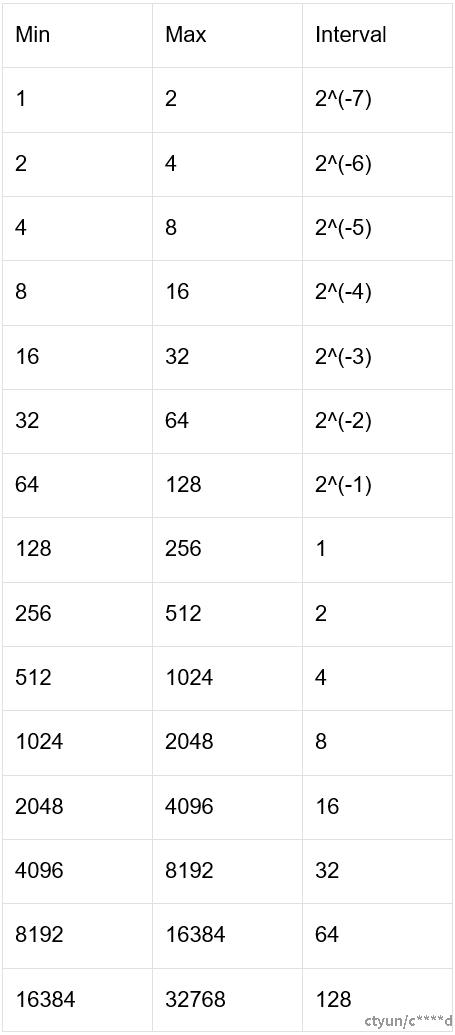
可以发现,浮点数在原点附近精度最高,可以达到2^(-m)。数值逐渐远离原点的同时,数值精度也逐渐下降。
3.2 float
Float数据又称为全精度数据,在计算机中使用32个二进制位也即2个字节来表示和存储,其由1位符号位、8位指数位和23位尾数位组成,明细如下:

于是,fp32的数据计算方式为:
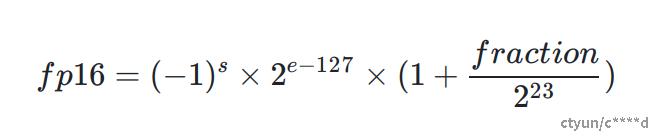
- 特殊情况-1 e为00000000
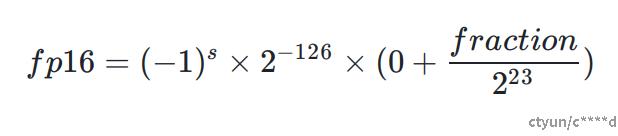
- 特殊情况-2 e为111111111
综上所述:
其中的精度表示在原点附近的精度,远离原点精度会降低!
3.3 fp16
Float16数据又称为半精度数据,在计算机中使用16个二进制位也即2个字节来表示和存储,其由1位符号位、5位指数位和10位尾数位组成,明细如下:

于是,fp16的数据计算方式为:
- 特殊情况-1 e为00000
- 特殊情况-2 e为111111
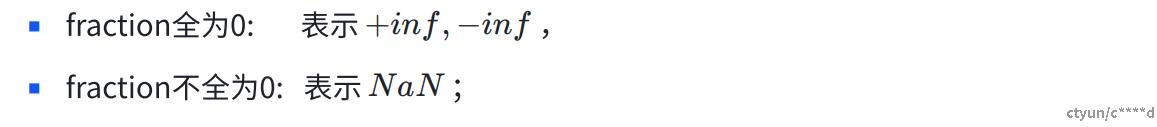
综上所述:
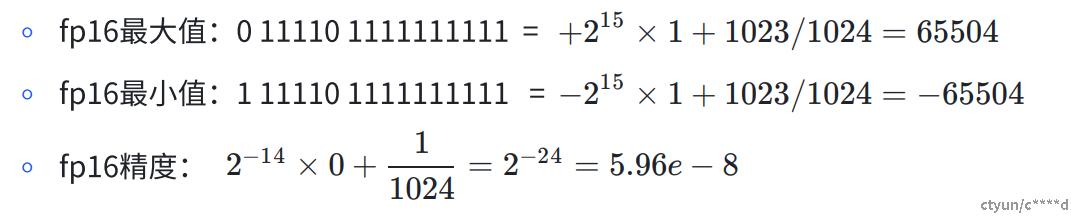
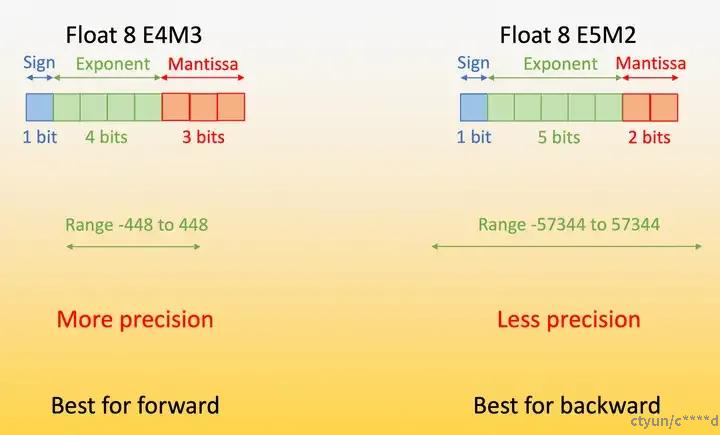
3.4 fp8
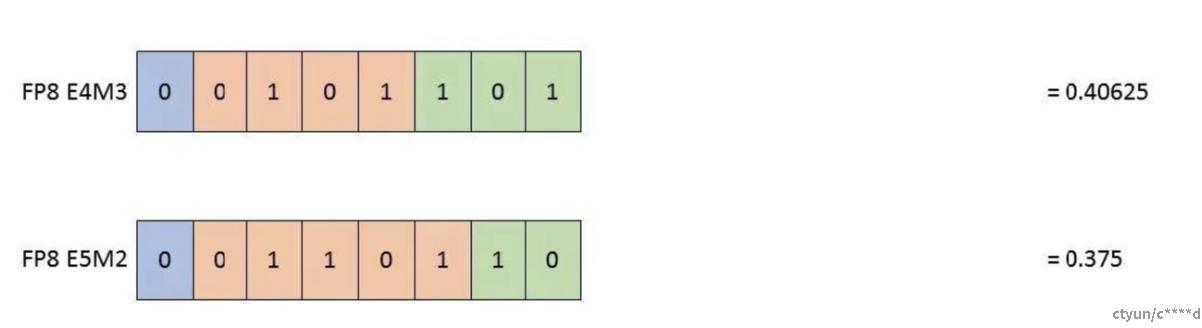
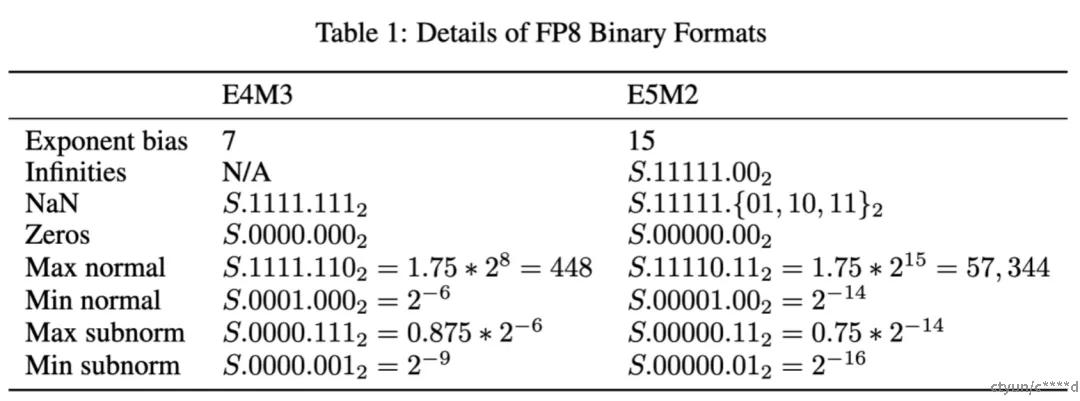
可以看到,因为FP8格式的设计遵循与IEEE-754约定保持一致的原则,只有在DL应用精度有望获得显著提高时才会偏离。因此,E5M2格式遵循IEEE754对指数和特殊值的约定,可视为IEEE半精度,但尾数位数较少(类似于bfloat16和TF32可视为IEEE单精度,但位数较少)。
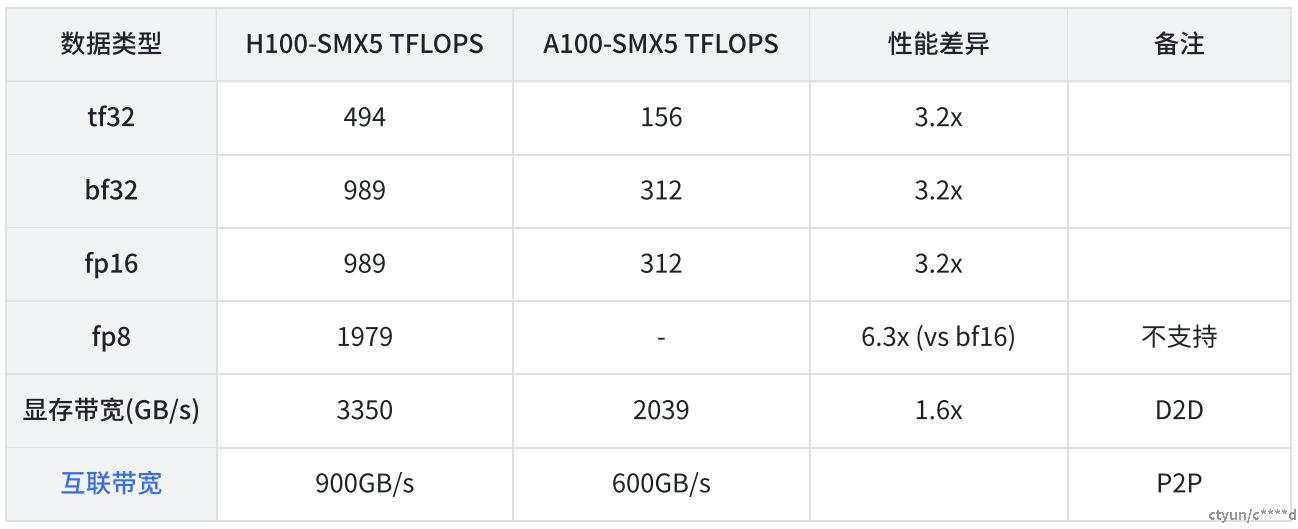
这使得E5M2和IEEEFP16格式之间可以直接转换。相比之下,E4M3的动态范围是通过回收用于特殊值的大部分比特模式来扩展,因为在这种情况下,所实现的更大范围要比支持特殊值的多种编码有用得多。如下表所示, 在 NVIDIA H100 Tensor Core GPU上为例,单位是TFLOPS,相较FP16和BF16,FP8的峰值性能能够实现翻倍:
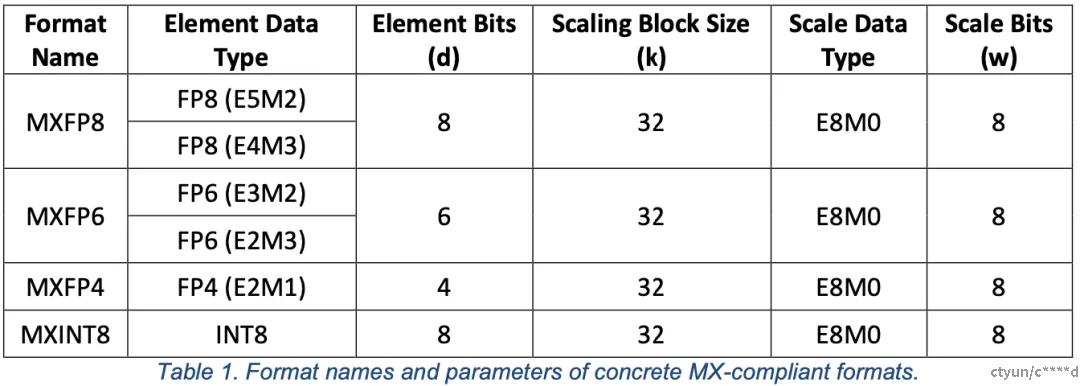
3.5 fp4/nf4
nf4全称为4-bit Fixed Point,指的是 4 位定点数格式。与浮点数不同,定点数使用固定的小数点位置来表示数值。这种格式对于需要固定精度和对计算效率要求较高的场景非常有用
3.6 总结
| 数据类型 | 比特位 | 符号位 | 指数位 | 尾数位 | 数值范围 | 数值精度 |
|---|---|---|---|---|---|---|
| double | 64 | 1 | 11 | 52 | -1.79e308~1.79e308 | 1e-15 |
| float | 32 | 1 | 8 | 23 | -3.4e38~3.4e38 | 1e-6 |
| tf32 | 19 | 1 | 8 | 10 | -3.4e38~3.4e38 | 1e-3 |
| fp16 | 16 | 1 | 5 | 10 | -65504~65504 | 1e-3 |
| bf16 | 16 | 1 | 8 | 7 | -3.39e38~3.39e38 | 1e-2 |
| fp8 | 8 | 1 | 5 | 2 | -57344~57344 | 0.25 |
| fp8 | 8 | 1 | 4 | 3 | -448~448 | 0.125 |
| fp8 | 8 | 1 | 4 | 3 | -240~240 | 0.125 |
| int | 32 | 1 | 31 | - | -2.15e9~2.15e9 | 1 |
| int16 | 16 | 1 | 15 | - | -32768~32767 | 1 |
| int8 | 8 | 1 | 7 | - | -128~127 | 1 |
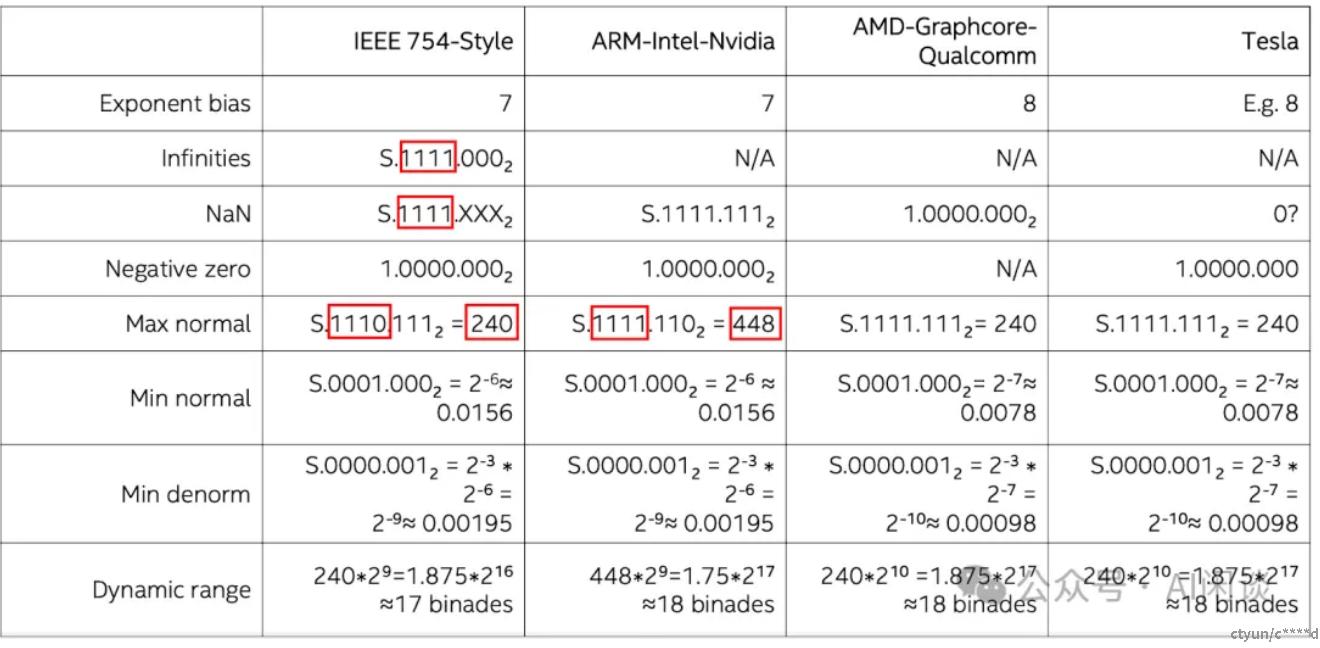
需要注意的是FP8有许多种类型,如下:

虽然都是 E5M2 或者 E4M3,不同公司的硬件可能采用不同的格式。比如 NVIDIA GPU 上的 E5M2 符合 IEEE 754 Style,而 E4M3 却不符合 IEEE 754 Style,本文中没有特殊说明都以 ARM-Intel-Nvidia Style 为例。如下图所示,IEEE 754 Style 的 E4M3 的范围为 [-240, 240],而 ARM-Intel-Nvidia Style 的 E4M3 的范围是 [-448, 448]:
4、Pytorch验证
import torch
print(torch.finfo(torch.float64))
#finfo(resolution=1e-15, min=-1.79769e+308, max=1.79769e+308, eps=2.22045e-16, tiny=2.22507e-308, dtype=float64)
print(torch.finfo(torch.float32))
# finfo(resolution=1e-06, min=-3.40282e+38, max=3.40282e+38, eps=1.19209e-07, tiny=1.17549e-38, dtype=float32)
print(torch.finfo(torch.float16))
# finfo(resolution=0.001, min=-65504, max=65504, eps=0.000976562, tiny=6.10352e-05, dtype=float16)
print(torch.finfo(torch.bfloat16))
# finfo(resolution=0.01, min=-3.38953e+38, max=3.38953e+38, eps=0.0078125, tiny=1.17549e-38, dtype=bfloat16)
print(torch.finfo(torch.float8_e5m2))
# finfo(resolution=1, min=-57344, max=57344, eps=0.25, smallest_normal=6.10352e-05, tiny=6.10352e-05, dtype=float8_e5m2)
print(torch.finfo(torch.float8_e5m2fnuz))
#finfo(resolution=1, min=-57344, max=57344, eps=0.125, smallest_normal=3.05176e-05, tiny=3.05176e-05, dtype=float8_e5m2fnuz)
print(torch.finfo(torch.float8_e4m3fnuz))
# finfo(resolution=1, min=-240, max=240, eps=0.125, smallest_normal=0.0078125, tiny=0.0078125, dtype=float8_e4m3fnuz)
print(torch.finfo(torch.float8_e4m3fn))
# finfo(resolution=1, min=-448, max=448, eps=0.125, smallest_normal=0.015625, tiny=0.015625, dtype=float8_e4m3fn)