49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs =["eat", "tea", "tan", "ate", "nat", "bat"]输出: [["bat"],["nat","tan"],["ate","eat","tea"]]示例 2:
输入: strs =[""]输出: [[""]]示例 3:
输入: strs =["a"]输出: [["a"]]
解题思路
可以使用哈希表来组织字母异位词。哈希表的键将是字符串中字母排序后的结果,而值则是具有相同字母组合的字符串列表。这样,所有的字母异位词都会被映射到相同的键下。具体步骤如下:
-
初始化哈希表:创建一个哈希表,用于存储每一组字母异位词。键为排序后的字符串,值为原字符串列表。
-
遍历字符串数组:对于数组中的每一个字符串:
- 将字符串中的字母进行排序。
- 检查排序后的字符串是否已经作为键存在于哈希表中。
- 如果存在,将原字符串添加到对应的列表中。
- 如果不存在,以排序后的字符串为键,创建一个新列表,并将原字符串添加到这个列表中。
-
收集结果:遍历哈希表,将所有的值(字符串列表)收集到一个结果列表中。
完整代码
python
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
anagrams = {}
for s in strs:
# 对字符串中的字符进行排序
sorted_str = ''.join(sorted(s))
# 如果排序后的字符串作为键存在,追加原字符串到对应的列表中
if sorted_str in anagrams:
anagrams[sorted_str].append(s)
# 否则,创建新的键值对
else:
anagrams[sorted_str] = [s]
# 返回哈希表中所有值组成的列表
return list(anagrams.values())Java
public class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
if (strs == null || strs.length == 0) return new ArrayList<>();
Map<String, List<String>> map = new HashMap<>();
for (String s : strs) {
char[] ca = s.toCharArray();
Arrays.sort(ca);
String keyStr = String.valueOf(ca);
if (!map.containsKey(keyStr)) map.put(keyStr, new ArrayList<>());
map.get(keyStr).add(s);
}
return new ArrayList<>(map.values());
}
public static void main(String[] args) {
Solution solution = new Solution();
String[] strs = {"eat", "tea", "tan", "ate", "nat", "bat"};
List<List<String>> result = solution.groupAnagrams(strs);
System.out.println(result);
}
}50. Pow(x, n)
实现 pow(x, n) ,即计算
x的整数n次幂函数(即,xn)。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000示例 2:
输入:x = 2.10000, n = 3 输出:9.26100示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
解题思路
实现 pow(x, n) 函数,我们可以利用"快速幂"算法以减少计算的次数。快速幂算法通过将指数折半分解,使得我们不必一步一步地乘以 x,而是可以快速达到目标指数。这个方法在处理非常大的指数时特别有效。
解题思路
-
特殊情况处理:如果
x为 0,直接返回 0(考虑到 0 的任何正指数都是 0)。如果n为 0,根据定义返回 1。 -
处理负指数:如果
n为负数,可以先计算x的-n次幂,然后取其倒数。这样可以转化为正指数的情况处理。 -
快速幂递归:使用递归函数计算
x^n。如果n是偶数,x^n可以分解为(x^(n/2))^2;如果n是奇数,则可以分解为x * (x^(n-1))。这样每次递归可以把问题规模减半,直到n为 1 或者特殊情况。 -
返回结果:根据上述递归过程计算结果。
完整代码
python
class Solution:
def myPow(self, x: float, n: int) -> float:
# 递归函数定义
def fastPow(x, n):
# 递归终止条件
if n == 0:
return 1.0
# 计算 x^(n/2)
half = fastPow(x, n // 2)
# 根据 n 的奇偶性返回结果
if n % 2 == 0:
return half * half
else:
return half * half * x
# 处理 n 为负的情况
if n < 0:
x = 1 / x
n = -n
# 调用快速幂函数
return fastPow(x, n)Java
public class Solution {
private double fastPow(double x, long n) {
if (n == 0) {
return 1.0;
}
double half = fastPow(x, n / 2);
if (n % 2 == 0) {
return half * half;
} else {
return half * half * x;
}
}
public double myPow(double x, int n) {
long N = n;
if (N < 0) {
x = 1 / x;
N = -N;
}
return fastPow(x, N);
}
public static void main(String[] args) {
Solution solution = new Solution();
double x = 2.00000;
int n = 10;
System.out.println(solution.myPow(x, n));
}
}51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中
'Q'和'.'分别代表了皇后和空位。
示例 1:
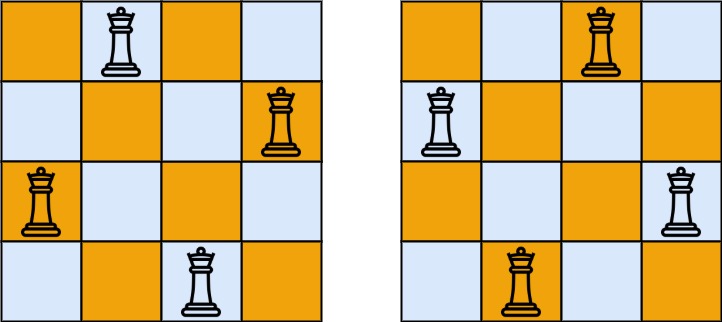
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1 输出:[["Q"]]
解题思路
解决 n 皇后问题通常使用回溯法,这是一种通过递归遍历所有可能情况来寻找所有解的算法。该问题的关键在于如何放置皇后以避免相互攻击,这意味着在同一行、同一列或者两个主要对角线上不能有两个皇后。
解题步骤
-
初始化棋盘:创建一个
n x n的棋盘,初始时全部填充为'.',表示所有位置都是空的。 -
递归放置皇后:从第一行开始,尝试在每一列放置一个皇后,然后检查当前放置是否会导致攻击。
检查当前位置是否安全:确保当前位置所在的列、左对角线和右对角线上没有其他皇后。对于对角线的检查,可以使用规律:在同一左对角线上的元素满足行号 - 列号 = 常数,在同一右对角线上的元素满足行号 + 列号 = 常数。 -
递归的继续与回溯:如果当前位置安全,则放置皇后,并递归地尝试放置下一个皇后。如果放置下一个皇后的所有可能都已尝试且不可行,或者已经放置了所有皇后,则回溯到上一步,移除当前皇后,尝试下一个位置。
-
保存解决方案:当成功放置了
n个皇后,即每一行都成功放置了一个皇后且没有冲突时,将当前棋盘的布局作为一个解决方案保存。 -
返回所有解决方案:重复以上步骤,直到遍历完所有可能的布局,返回所有有效的棋盘布局。
完整代码
python
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
def could_place(row, col):
return not (cols[col] + hill_diagonals[row - col] + dale_diagonals[row + col])
def place_queen(row, col):
queens.add((row, col))
cols[col] = 1
hill_diagonals[row - col] = 1
dale_diagonals[row + col] = 1
def remove_queen(row, col):
queens.remove((row, col))
cols[col] = 0
hill_diagonals[row - col] = 0
dale_diagonals[row + col] = 0
def add_solution():
solution = []
for _, col in sorted(queens):
solution.append('.' * col + 'Q' + '.' * (n - col - 1))
output.append(solution)
def backtrack(row=0):
for col in range(n):
if could_place(row, col):
place_queen(row, col)
if row + 1 == n:
add_solution()
else:
backtrack(row + 1)
remove_queen(row, col)
cols = [0] * n
hill_diagonals = [0] * (2 * n - 1)
dale_diagonals = [0] * (2 * n - 1)
queens = set()
output = []
backtrack()
return outputJava
public class Solution {
// 定义记录每一行皇后位置的数组
int[] queens;
// 定义标记是否可以攻击的辅助数组
boolean[] cols;
boolean[] diag1;
boolean[] diag2;
// 存储最终结果的列表
List<List<String>> output = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
queens = new int[n];
cols = new boolean[n];
diag1 = new boolean[2 * n - 1];
diag2 = new boolean[2 * n - 1];
backtrack(0, n);
return output;
}
private void backtrack(int row, int n) {
if (row == n) {
// 所有皇后都放置完毕,添加到结果列表
List<String> board = generateBoard(queens, n);
output.add(board);
return;
}
for (int col = 0; col < n; col++) {
if (isNotUnderAttack(row, col, n)) {
placeQueen(row, col, n);
backtrack(row + 1, n);
removeQueen(row, col, n);
}
}
}
private boolean isNotUnderAttack(int row, int col, int n) {
return !cols[col] && !diag1[row - col + n - 1] && !diag2[row + col];
}
private void placeQueen(int row, int col, int n) {
queens[row] = col;
cols[col] = true;
diag1[row - col + n - 1] = true;
diag2[row + col] = true;
}
private void removeQueen(int row, int col, int n) {
queens[row] = 0;
cols[col] = false;
diag1[row - col + n - 1] = false;
diag2[row + col] = false;
}
private List<String> generateBoard(int[] queens, int n) {
List<String> board = new ArrayList<>();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
java.util.Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
public static void main(String[] args) {
Solution solution = new Solution();
List<List<String>> results = solution.solveNQueens(4);
for (List<String> board : results) {
for (String row : board) {
System.out.println(row);
}
System.out.println();
}
}
}