97. 交错字符串,100. 相同的树,101. 对称二叉树,每题做详细思路梳理,配套Python&Java双语代码, 2024.03.245可通过leetcode所有测试用例。
97. 交错字符串
给定三个字符串
s1、s2、s3,请你帮忙验证s3是否是由s1和s2交错 组成的。两个字符串
s和t交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空子字符串
:
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1- 交错 是
s1 + t1 + s2 + t2 + s3 + t3 + ...或者t1 + s1 + t2 + s2 + t3 + s3 + ...注意:
a + b意味着字符串a和b连接。
示例 1:
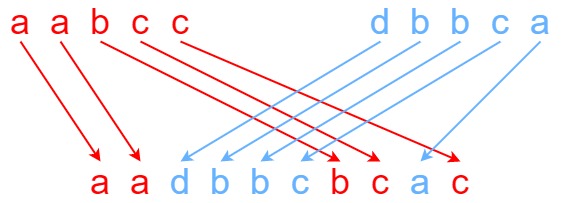
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" 输出:true示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" 输出:false示例 3:
输入:s1 = "", s2 = "", s3 = "" 输出:true
解题思路
要解决这个问题,我们可以使用动态规划的方法。动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。具体到这个问题,我们可以定义一个二维的动态规划数组 dp[i][j],其中 dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符是否能交错组成 s3 的前 i + j 个字符。
-
初始化:首先,如果
s1和s2的长度之和不等于s3的长度,那么s3必然不可能由s1和s2交错组成,直接返回false。否则,初始化动态规划数组dp,其中dp[0][0]为true,表示空字符串是由两个空字符串交错组成的。 -
处理
s1:对于dp[i][0](即只考虑s1),如果s1的前i个字符和s3的前i个字符相同,并且dp[i-1][0]为true,那么dp[i][0]也为true。 -
处理
s2:类似地,对于dp[0][j](即只考虑s2),如果s2的前j个字符和s3的前j个字符相同,并且dp[0][j-1]为true,那么dp[0][j]也为true。 -
填充剩余的
dp数组:对于dp[i][j],如果dp[i-1][j]是true且s1[i-1]等于s3[i+j-1],则dp[i][j]也是true;或者如果dp[i][j-1]是true且s2[j-1]等于s3[i+j-1],则dp[i][j]也是true。 -
返回结果:最终,
dp[len(s1)][len(s2)]的值将表示s3是否可以由s1和s2交错组成。
完整代码
Python
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
if len(s1) + len(s2) != len(s3):
return False
dp = [[False] * (len(s2) + 1) for _ in range(len(s1) + 1)]
dp[0][0] = True
for i in range(1, len(s1) + 1):
dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]
for j in range(1, len(s2) + 1):
dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]
for i in range(1, len(s1) + 1):
for j in range(1, len(s2) + 1):
dp[i][j] = (dp[i - 1][j] and s1[i - 1] == s3[i + j - 1]) or \
(dp[i][j - 1] and s2[j - 1] == s3[i + j - 1])
return dp[len(s1)][len(s2)]Java
public class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
if (s1.length() + s2.length() != s3.length()) {
return false;
}
boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];
dp[0][0] = true;
for (int i = 1; i <= s1.length(); i++) {
dp[i][0] = dp[i - 1][0] && s1.charAt(i - 1) == s3.charAt(i - 1);
}
for (int j = 1; j <= s2.length(); j++) {
dp[0][j] = dp[0][j - 1] && s2.charAt(j - 1) == s3.charAt(j - 1);
}
for (int i = 1; i <= s1.length(); i++) {
for (int j = 1; j <= s2.length(); j++) {
dp[i][j] = (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) ||
(dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
}
}
return dp[s1.length()][s2.length()];
}
}
100. 相同的树
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
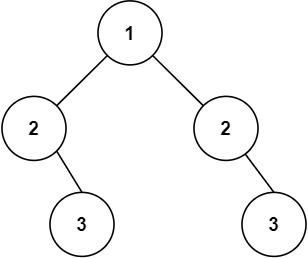
示例 1:
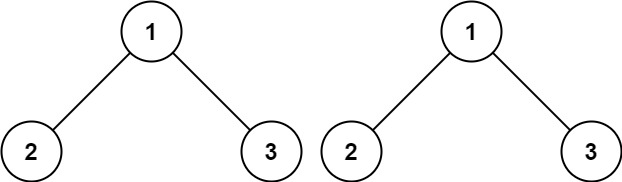
输入:p = [1,2,3], q = [1,2,3] 输出:true示例 2:
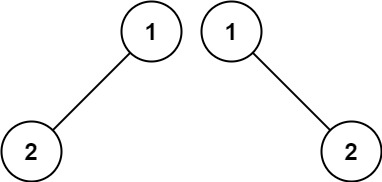
输入:p = [1,2], q = [1,null,2] 输出:false示例 3:
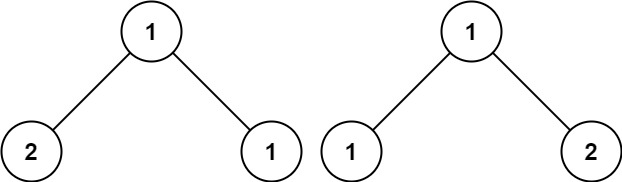
输入:p = [1,2,1], q = [1,1,2] 输出:false
解题思路
要检验两棵二叉树是否相同,我们可以递归地比较每一个节点。对于每一对节点,我们需要比较它们的值是否相同,并且它们的左子节点和右子节点也分别相同。
-
终止条件:如果两个节点都是
null,那么它们相同,返回true。如果其中一个是null而另一个不是,那么它们不同,返回false。 -
比较节点值:如果两个节点都非空,比较它们的值。如果值不相同,返回
false。 -
递归比较子节点:递归地比较左子节点和右子节点。如果左子节点或右子节点中的任何一个对比返回
false,则整个树不相同。 -
返回结果:如果所有对比都相同,则返回
true。
完整代码
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
# 如果两个节点都是 None,那么它们相同
if not p and not q:
return True
# 如果一个节点是 None,另一个不是,或者两个节点的值不同,那么它们不相同
if not p or not q or p.val != q.val:
return False
# 递归比较左子树和右子树
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) return true;
if (p == null || q == null) return false;
if (p.val != q.val) return false;
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
101. 对称二叉树
给你一个二叉树的根节点
root, 检查它是否轴对称。
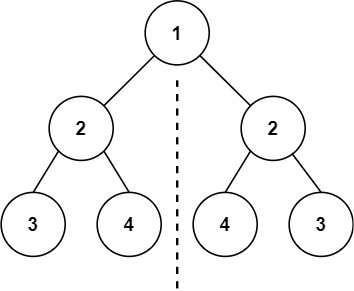
示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内-100 <= Node.val <= 100
解题思路
要检查一棵二叉树是否是轴对称的,我们可以递归地检查树的两个子树。对于树的两个子树来说,它们要成为镜像对称,必须满足以下条件:
- 它们的根节点具有相同的值。
- 每个树的右子树都与另一棵树的左子树镜像对称。
具体步骤
-
初始化:如果树是空的,则它是对称的。
-
递归函数:创建一个递归函数
isMirror(t1, t2)来检查两个树t1和t2是否是镜像对称的。在这个函数中:- 如果
t1和t2都为空,返回True(它们是对称的)。 - 如果
t1或t2其中之一为空,或者它们的值不相等,返回False。 - 递归检查
t1的左子树与t2的右子树是否对称,以及t1的右子树与t2的左子树是否对称。
- 如果
-
调用递归函数:从根节点开始调用递归函数,即
isMirror(root.left, root.right)。
完整代码
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
# 用于递归检查两个树是否为镜像对称
def isMirror(t1: TreeNode, t2: TreeNode) -> bool:
# 如果两个节点都为空,则它们是对称的
if not t1 and not t2:
return True
# 如果其中一个为空,另一个不为空,则它们不对称
if not t1 or not t2:
return False
# 检查当前节点的值是否相同,并递归检查左子树和右子树
return (t1.val == t2.val) and isMirror(t1.right, t2.left) and isMirror(t1.left, t2.right)
# 从根节点的两个子节点开始递归检查
return isMirror(root, root)Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public boolean isSymmetric(TreeNode root) {
return root == null || isMirror(root.left, root.right);
}
private boolean isMirror(TreeNode t1, TreeNode t2) {
// 如果两个节点都为空,那么它们是对称的
if (t1 == null && t2 == null) return true;
// 如果一个为空另一个不为空,或者两个节点的值不相同,那么它们不对称
if (t1 == null || t2 == null || t1.val != t2.val) return false;
// 递归比较t1的左子树与t2的右子树和t1的右子树与t2的左子树是否对称
return isMirror(t1.left, t2.right) && isMirror(t1.right, t2.left);
}
}