题目：
给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

示例 1:

输入: 1
输出: true
解释: 20 = 1

示例 2:

输入: 16
输出: true
解释: 24 = 16

示例 3:

输入: 218
输出: false

---

思路一:
使用常规解题思路

class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n<1)return false;
        while(n%2==0){
            n=n/2;
        }
        if(n==1)return true;
        else return false;
    }
}

此处的if(n==1)return true; else return false;
可以直接更换为return n==1；（相同意思）
思路二：
使用递归的方式

class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n<1)return false;
        if(n==1)return true;
        return isPowerOfTwo(n/2)&&n%2==0;
    }
}

思路三：
在int类型中 只有32位，即单独每一位都是1的时候，才是2的幂
去掉一个符号位最高位，即遍历31次既可以，在依次往左移位
这种位运算方法不错，可记住

class Solution {
    public boolean isPowerOfTwo(int n) {
     int tmp = 1;
        for (int i = 0; i < 31; i++) {
            if (tmp == n) {
                return true;
            }
            tmp <<= 1;
        }
        return false;
    }
}

思路四：

=-=想不到
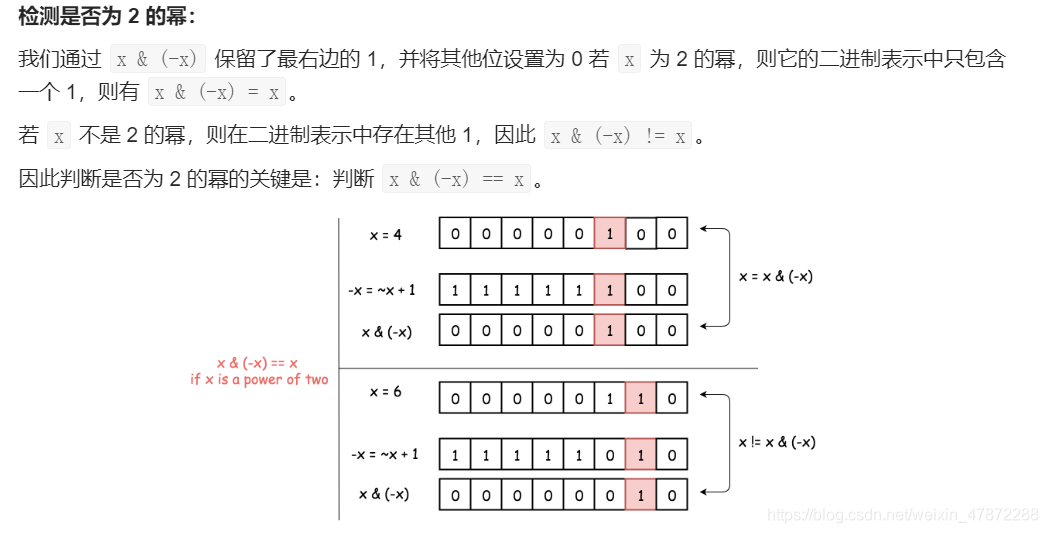
通过补码与原码的相与是否是本身，如果是则只有1个1
如果不是则还有其他位置的1
(x & (-x)) == x;

class Solution {
  public boolean isPowerOfTwo(int n) {
    if (n == 0) return false;
    long x = (long) n;
    return (x & (-x)) == x;
  }
}

思路五：
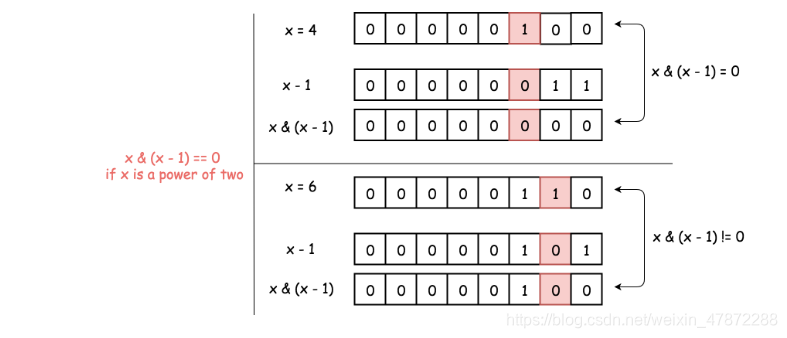
使用位运算x& (x - 1)可以将最右边的1设置为0。
(x - 1)代表了将x最右边的1设置为0，并且将较低位设置为1
再使用与运算:则x最右边的1和就会被设置为0，因为1 &0 = 0。

class Solution {
  public boolean isPowerOfTwo(int n) {
    if (n == 0) return false;
    long x = (long) n;
    return (x & (x - 1)) == 0;
  }
}

总结：

• 常规逻辑思路
• 递归
• 移位判断是否位1
• 源码与补码相与判断
• 与前一位想与