迪杰斯特拉算法(Dijkstra's Algorithm),又称为狄克斯特拉算法,是一种用于解决带权重有向图或无向图最短路径问题的算法。该算法由荷兰计算机科学家艾兹赫尔·狄克斯特拉在1956年发明,是一种广泛应用于网络路由和其他领域的算法。
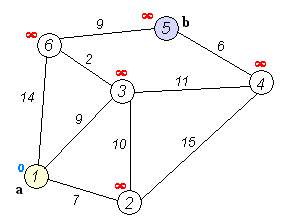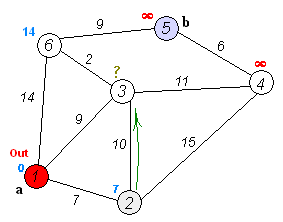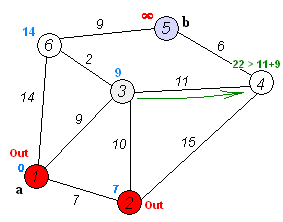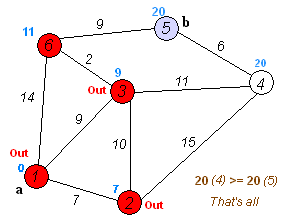
假设有如下的图示例,包含6个节点和它们之间的边:
节点: 0 1 2 3 4 5
边: (0, 1, 4), (0, 2, 2), (1, 3, 2), (1, 2, 1), (2, 3, 5), (2, 4, 6), (3, 4, 1), (3, 5, 3), (4, 5, 4)现在,我们设定起点为节点0,终点为节点5。让我们通过迪杰斯特拉算法来找到起点0到终点5的最短路径。
首先,我们初始化距离数组dist和前驱数组prev:
dist: [0, INF, INF, INF, INF, INF]
prev: [-1, -1, -1, -1, -1, -1]然后,我们从起点0开始,将其加入集合S,并更新与起点相邻的节点的最短距离和前驱节点。
迭代1:节点0的邻接节点是节点1和节点2,它们与起点0的距离分别为4和2。由于这两个距离比当前已知的距离要小,所以我们更新dist和prev:
dist: [0, 4, 2, INF, INF, INF]
prev: [-1, 0, 0, -1, -1, -1]迭代2:下一步我们需要选择距离起点0最近的节点,也就是节点2(距离为2)。将节点2加入集合S,并更新与节点2相邻的节点的最短距离和前驱节点。
节点2的邻接节点是节点1、节点3和节点4,它们与起点的距离分别为3、7和8。由于节点1的距离比当前已知的距离要小,所以我们更新dist和prev:
dist: [0, 3, 2, INF, INF, INF]
prev: [-1, 2, 0, -1, -1, -1]迭代3:下一步选择距离起点0最近的节点,也就是节点1(距离为3)。将节点1加入集合S,并更新与节点1相邻的节点的最短距离和前驱节点。
节点1的邻接节点是节点3和节点2,它们与起点的距离分别为5和4。由于节点3的距离比当前已知的距离要小,所以我们更新dist和prev:
dist: [0, 3, 2, 5, INF, INF]
prev: [-1, 2, 0, 1, -1, -1]迭代4:下一步选择距离起点0最近的节点,也就是节点3(距离为5)。将节点3加入集合S,并更新与节点3相邻的节点的最短距离和前驱节点。
节点3的邻接节点是节点4和节点5,它们与起点的距离分别为6和8。由于节点4的距离比当前已知的距离要小,所以我们更新dist和prev:
dist: [0, 3, 2, 5, 7, INF]
prev: [-1, 2, 0, 1, 3, -1]迭代5:下一步选择距离起点0最近的节点,也就是节点4(距离为7)。将节点4加入集合S,并更新与节点4相邻的节点的最短距离和前驱节点。
节点4的邻接节点是节点3和节点5,它们与起点的距离分别为6和11。由于节点3的距离比当前已知的距离要小,所以我们更新dist和prev:
dist: [0, 3, 2, 5, 6, INF]
prev: [-1, 2, 0, 1, 3, 4]迭代6:最后一个节点是终点5,我们将其加入集合S,并完成算法。
此时,起点0到终点5的最短路径为:0 -> 2 -> 1 -> 3 -> 4 -> 5,总距离为6。
这就是迪杰斯特拉算法的演示过程。通过不断更新最短距离和前驱节点,我们可以找到起点到终点的最短路径。
三、 算法优化
尽管迪杰斯特拉算法已经在实践中证明了其效率和可靠性,但它仍然存在一些优化空间,以进一步提高算法效率。
堆优化
上面我们介绍的算法实现方式使用了小根堆来存储节点编号和距离信息。这样做可以确保我们每次取出的节点都是距离起点最近的。但在节点数较多的情况下,堆的维护和调整成本会很高,影响算法效率。
针对这个问题,我们可以采用更快的数据结构来存储节点信息。例如,我们可以使用斐波那契堆(Fibonacci Heap)或二项堆(Binomial Heap)等高效的堆实现方式来优化算法。
并行计算
迪杰斯特拉算法是一种基于图的算法,因此可以将其分布式计算,以提高计算效率。
例如,我们可以利用MapReduce等分布式计算框架,在多个计算节点上并行执行迪杰斯特拉算法,并在最后将结果汇总。通过这种方式,我们可以显著缩短计算时间,提高算法效率。
基于GPU的优化
由于迪杰斯特拉算法涉及大量的图数据处理和距离计算,因此GPU(Graphics Processing Unit)可以被用来加速算法运行。通过将算法并行化,将图划分到多个GPU处理单元上,我们可以显著提高算法效率。
四、 结论
迪杰斯特拉算法是一种用于解决带权重有向图或无向图最短路径问题的经典算法。该算法基于贪心策略,通过不断扩展已知的最短路径来逐步得到起点到其他所有点的最短路径。
在实际应用中,我们常常需要对算法进行优化,以提升算法效率和性能。例如,我们可以采用更快的堆实现方式、并行计算和GPU加速等方法,以进一步提高算法效率。

