1.简单选择排序

1.排序思路

简单选择排序的基本思想是第i趟排序开始时，当前有序区和无序区分别为$R[\mathrm{0..}i-1]$$R[i..n-1](0\le i<n-1)$,该趟排序是从当前无序区中选出值最小的元素$R[k]$,将它与无序区的第一个元素$R[i]$交换，使$R[\mathrm{0..}i]$和$R[i+\mathrm{1..}n-1]$分别变为新的有序区和新的无序区。
实现步骤如下所示：
1、第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置。
2、然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。
3、以此类推，直到全部待排序的数据元素的个数为零。
具体过程如下图所示：以数组[4,3,8,5,2,6,1,7]为例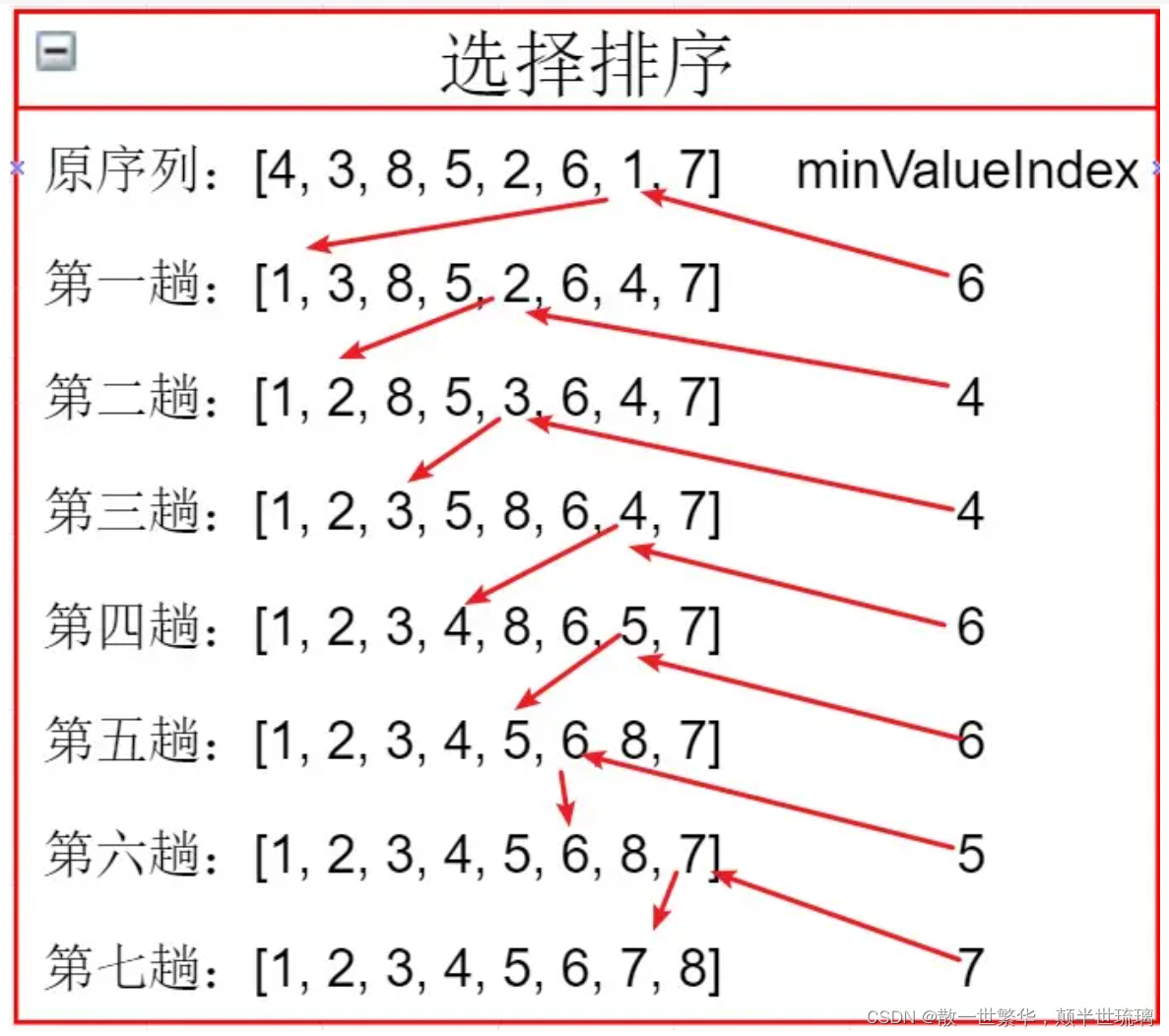

2.排序算法

void SelectSort(int R[],int n) {
	int i, j, k;
	for (i = 0; i < n - 1; i++) {//做第i趟排序
		k = i;
		for (j = i + 1; j < n; j++) {
			if (R[j] < R[k]) {
				k = j;//k记录目前找到的最小值的索引
			}
		}
		if (k != i)
			swap(R[k], R[i]);//交换元素
	}
}//简单选择排序

int main() {
	int R[] = { 4,5,6,3,2,1 };
	SelectSort(R,6);
	for (int i = 0; i < 6; i++) {
		printf("%d ", R[i]);
	}
	return 0;
}

3.算法分析

时间复杂度：平均 O ( n 2 ) O(n^2) O(n2) 最好 O ( n 2 ) O(n^2) O(n2) 最差 O ( n 2 ) O(n^2) O(n2)
空间复杂度：$O(1)$
稳定性:不稳定
复杂性:简单

2.堆排序

1.排序思路

堆排序（heap sort）是一种树形选择排序方法，它的特点是将$R[\mathrm{1..}n]$看成是一颗完全二叉树的顺序存储结构。利用完全二叉树中的双亲结点和孩子结点之间的位置关系在无序区中选择值最大或最小的元素。
性质：每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆；每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。如下图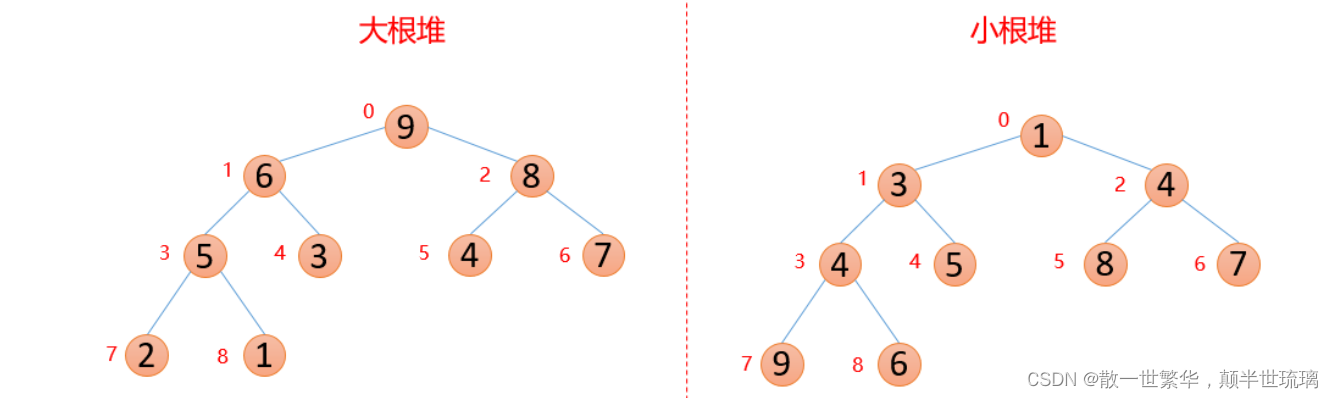


堆排序实现的关键就是筛选，其过程是假如完全二叉树的根节点是$R[i]$,它的左右子树已是大根堆，将其两个孩子的值$R[2i]、R[2i+1]$比较，将二者的较大者与$R[i]$比较，若$R[]i$较小，将其与最大孩子进行交换，这就有可能破坏下一级的堆，继续采用上述方法构造下一级的堆，直至这棵完全二叉树变成一个大根堆为止。
此时根节点$R[i]$一定是最大值的节点，将其放到排序序列的最后，也就是将堆中的跟与最后一个叶子交换。由于最大元素已归位，整个待排序的元素个数减少一个。由于根节点的改变，则$n-1$个节点$R[\mathrm{1..}n-1]$不一定是对，但其左子树和右子树均为堆，在重复上述变为大根堆的过程，将其根节点变为次大的元素，在将其放到排序xulde倒数第二个位置，即堆中的跟与最后一个叶子交换，待排序的元素个数变为$n-2$个，即$R[\mathrm{1..}n-2]$，在调整，再将根节点归位，如此这样，直至二叉树剩下一个根为止，即实现了堆排序。

2.排序算法

void sift(int R[], int low, int high) {
	int i = low, j = 2 * i;
	int tem = R[i];
	while (j <= high) {
		if (j < high && R[j] < R[j + 1])
			j++;
		if (tem < R[j]) {
			R[i] = R[j];
			i = j;//修改i和j的值 以便于继续向下筛选
			j = 2 * i;
		}
		else break;
	}
	R[i] = tem;//被筛选结点放入最终位置上
}

void HeapSort(int R[],int n) {
	int i;
	for (i = n / 2; i >= 0; i--) //循环建立初始堆
		sift(R, i, n);
	for (i = n-1; i >= 1; i--) {
		swap(R[0], R[i]);
		sift(R,0, i - 1);
	}
}

int main() {
	int R[] = { 4,5,6,3,2,1 };
	HeapSort(R,6);
	for (int i = 0; i < 6; i++) {
		printf("%d ", R[i]);
	}
	return 0;
}

3.算法分析

时间复杂度：最好 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2​n),最坏 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2​n)，平均 O ( n l o g 2 n ) O(nlog_{2}n) O(nlog2​n)
空间复杂度：$O(1)$
稳定性：不稳定
复杂性：较复杂