和前面的系列不同，布谷鸟这里没有现成的Python的包，使用我们需要自己写各种源码模块进行组合，达到布谷鸟搜索算法（CS）的功能。

这里的CS算法是面向过程的编程，都是自定义函数，不涉及类与对象。还是很简单的，知道原理的话可以看得懂的。

---

布谷鸟代码

# cuckoo_search via levy flight for global optimization
import numpy as np
import scipy.special as sc_special
import random
import time

time_start = time.time()  # 记录开始时间
#a=[]
#生成莱维飞行的步长
def levy_flight(n, m, beta):
    """
    This function implements Levy's flight.
    ---------------------------------------------------
    Input parameters:
        n: Number of steps 
        m: Number of dimensions
        beta: Power law index (note: 1 < beta < 2)
    Output:
        'n' levy steps in 'm' dimension
    """
    sigma_u = (sc_special.gamma(1+beta)*np.sin(np.pi*beta/2)/(sc_special.gamma((1+beta)/2)*beta*(2**((beta-1)/2))))**(1/beta)
    sigma_v = 1

    u =  np.random.normal(0, sigma_u, (n, m))
    v = np.random.normal(0, sigma_v, (n, m))
    steps = u/((np.abs(v))**(1/beta))

    return steps

#计算每个鸟巢的适应值（即函数值）
def calc_fitness(fit_func, nests):
    """
    calculate each nest's fitness
    ---------------------------------------------------
    Input parameters:
        fit_func: User defined fitness evaluative function
        nests:  Nests' locations
    Output:
        Every nest's fitness
    """
    n, m = nests.shape
    fitness = np.empty(n)

    for each_nest in range(n):
        fitness[each_nest] = fit_func(nests[each_nest])

    return fitness

#产生鸟巢的位置
def generate_nests(n, m, lower_boundary, upper_boundary):
    """
    Generate the nests' locations
    ---------------------------------------------------
    Input parameters:
        n: Number of nests
        m: Number of dimensions
        lower_boundary: Lower bounary (example: lower_boundary = (-2, -2, -2))
        upper_boundary: Upper boundary (example: upper_boundary = (2, 2, 2))
    Output:
        generated nests' locations
    """
    lower_boundary = np.array(lower_boundary)
    upper_boundary = np.array(upper_boundary)
    nests = np.empty((n, m))

    for each_nest in range(n):
        nests[each_nest] = lower_boundary + np.array([np.random.rand() for _ in range(m)]) * (upper_boundary - lower_boundary)

    return nests

#更新鸟巢的位置
def update_nests(fit_func, lower_boundary, upper_boundary, nests, best_nest, fitness, step_coefficient):
    """
    This function is to get new nests' locations and use new better one to replace the old nest
    ---------------------------------------------------
    Input parameters:
        fit_func: User defined fitness evaluative function
        lower_boundary: Lower bounary (example: lower_boundary = (-2, -2, -2))
        upper_boundary: Upper boundary (example: upper_boundary = (2, 2, 2))
        nests: Old nests' locations 
        best_nest: Nest with best fitness
        fitness: Every nest's fitness
        step_coefficient:  Step size scaling factor related to the problem's scale (default: 0.1)
    Output:
        Updated nests' locations
    """
    lower_boundary = np.array(lower_boundary)
    upper_boundary = np.array(upper_boundary)
    n, m = nests.shape
    # generate steps using levy flight
    steps = levy_flight(n, m, 1.5)
    new_nests = nests.copy()

    for each_nest in range(n):
        # coefficient 0.01 is to avoid levy flights becoming too aggresive
        # and (nest[each_nest] - best_nest) could let the best nest be remained
        step_size = step_coefficient * steps[each_nest] * (nests[each_nest] - best_nest)
        step_direction = np.random.rand(m)
        new_nests[each_nest] += step_size * step_direction
        # apply boundary condtions
        new_nests[each_nest][new_nests[each_nest] < lower_boundary] = lower_boundary[new_nests[each_nest] < lower_boundary]
        new_nests[each_nest][new_nests[each_nest] > upper_boundary] = upper_boundary[new_nests[each_nest] > upper_boundary]

    new_fitness = calc_fitness(fit_func, new_nests)
    nests[new_fitness > fitness] = new_nests[new_fitness > fitness]
    
    return nests

#按照一定概率抛弃鸟蛋，换巢（局部搜索）
def abandon_nests(nests, lower_boundary, upper_boundary, pa):
    """
    Some cuckoos' eggs are found by hosts, and are abandoned.So cuckoos need to find new nests.
    ---------------------------------------------------
    Input parameters:
        nests: Current nests' locations
        lower_boundary: Lower bounary (example: lower_boundary = (-2, -2, -2))
        upper_boundary: Upper boundary (example: upper_boundary = (2, 2, 2))
        pa: Possibility that hosts find cuckoos' eggs
    Output:
        Updated nests' locations
    """
    lower_boundary = np.array(lower_boundary)
    upper_boundary = np.array(upper_boundary)
    n, m = nests.shape
    for each_nest in range(n):
        if (np.random.rand() < pa):
            step_size = np.random.rand() * (nests[np.random.randint(0, n)] - nests[np.random.randint(0, n)])
            nests[each_nest] += step_size
            # apply boundary condtions
            nests[each_nest][nests[each_nest] < lower_boundary] = lower_boundary[nests[each_nest] < lower_boundary]
            nests[each_nest][nests[each_nest] > upper_boundary] = upper_boundary[nests[each_nest] > upper_boundary]
    
    return nests

#算法迭代
def cuckoo_search(n, m, fit_func, lower_boundary, upper_boundary, iter_num = 1000,pa = 0.25, beta = 1.5, step_size = 0.01):
    """
    Cuckoo search function
    ---------------------------------------------------
    Input parameters:
        n: Number of nests
        m: Number of dimensions
        fit_func: User defined fitness evaluative function
        lower_boundary: Lower bounary (example: lower_boundary = (-2, -2, -2))
        upper_boundary: Upper boundary (example: upper_boundary = (2, 2, 2))
        iter_num: Number of iterations (default: 100) 
        pa: Possibility that hosts find cuckoos' eggs (default: 0.25)
        beta: Power law index (note: 1 < beta < 2) (default: 1.5)
        step_size:  Step size scaling factor related to the problem's scale (default: 0.1)
    Output:
        The best solution and its value
    """
    # get initial nests' locations 
    nests = generate_nests(n, m, lower_boundary, upper_boundary)
    fitness = calc_fitness(fit_func, nests)

    # get the best nest and record it
    best_nest_index = np.argmin(fitness)
    best_fitness = fitness[best_nest_index]
    best_nest = nests[best_nest_index].copy()

    for _ in range(iter_num):
        nests = update_nests(fit_func, lower_boundary, upper_boundary, nests, best_nest, fitness, step_size)
        nests = abandon_nests(nests, lower_boundary, upper_boundary, pa)
        fitness = calc_fitness(fit_func, nests)
        
        min_nest_index = np.argmin(fitness)
        min_fitness = fitness[min_nest_index]
        min_nest = nests[min_nest_index]
        a.append(min_fitness)

        if (min_fitness < best_fitness):
            best_nest = min_nest.copy()
            best_fitness = min_fitness

    return (best_nest, best_fitness)

上述代码都是拆分为一个个小函数。最后的cuckoo_search是总体的搜索迭代的函数。

对布谷鸟算法的搜索能力，我们采用 Goldstein-Price函数进行测试。Goldstein-Price函数是二元八次多项式，是一个常见的用来进行算法测试的函数，可以用算法找它的局部最小值。该函数理论在x=0,y=-1处取得最小值3，该函数的公式如下：

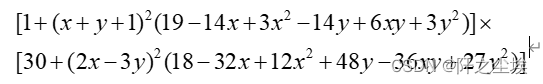
进行定义和计算

if __name__=='__main__':
    def fit_func(nest):
        x= nest        
        #return 3*(1-x)**2*np.e**(-x**2-(y+1)**2) - 10*(x/5-x**3-y**5)*np.e**(-x**2-y**2) - (np.e**(-(x+1)**2-y**2))/3
        return  (1+pow((1+x[0]+x[1]),2)*(19-14*x[0]+3*x[0]*x[0]-14*x[1]+6*x[0]*x[1]+3*x[1]*x[1]))*(30+pow((2*x[0]-3*x[1]),2)*(18-32*x[0]+12*x[0]*x[0]+48*x[1]-36*x[0]*x[1]+27*x[1]*x[1]))

    best_nest, best_fitness = cuckoo_search(100, 2, fit_func, [-3, -3], [3, 3],iter_num = 1000, step_size = 0.1)

    time_end = time.time()  # 记录结束时间
    time_sum = time_end - time_start  # 计算的时间差为程序的执行时间，单位为秒/s
    print(time_sum)
    print('最小值为:%.5f, 在(%.5f, %.5f)处取到!'%(best_fitness, best_nest[0], best_nest[1]))

 可以看到迭代1000次用时4s，还是很快的。和理论的最小值3很接近，x1和x2的值和真实值也还比较接近。

想复用这段代码到别的问题只需要改最后的这个fit_func()就行，返回你要评价的指标，布谷鸟会自动找最小值，并且告诉你参数为多少时取到。