加权最小二乘 的思想是在最小二乘上进行了改进。从损失函数角度来看，就是在每个样本的误差平方和求和之前，给每个误差平方赋予了一个权重，这个权重有很多种取法。可以把那残差平方的倒数作为权重。这样就可以让误差大的样本对于损失函数的影响较小，不受极端值的影响，拟合效果可以更好。

本次使用人工数据集，仿真实验。人工生成的数据集的好处就是可以自己给数据加你想要的扰动项，可以加上异方差。然后回归系数的真实值你是知道的，所以就很方便验证模型的拟合能力。

---

导入包

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from scipy import stats
from statsmodels.iolib.table import SimpleTable, default_txt_fmt

np.random.seed(1024)

生成人工数据 

生成X

nsample = 100
x = np.linspace(1, 100, nsample)
#X = np.column_stack((x, (x - 5) ** 2))      #抛物线数据
X = sm.add_constant(X)                       #添加常数列
X[:5]

 生成y

beta = [5.0, 0.5, ]#-0.01]
y_true = np.dot(X, beta)
y_true

 可以看到y是为y=5+0.5x，这是实际的方程。

添加扰动项

#添加残差
sig = 0.75
w = np.linspace(1, 10, nsample)
e = np.random.normal(size=nsample)
e=sig * w * e
y = y_true + e
X = X[:, [0, 1]]

W为扰动项的大小程度 ，我们让它线性增大，即x越大，残差的波动也越大。

画图查看

plt.figure(figsize=(6,4))
plt.scatter(x,y)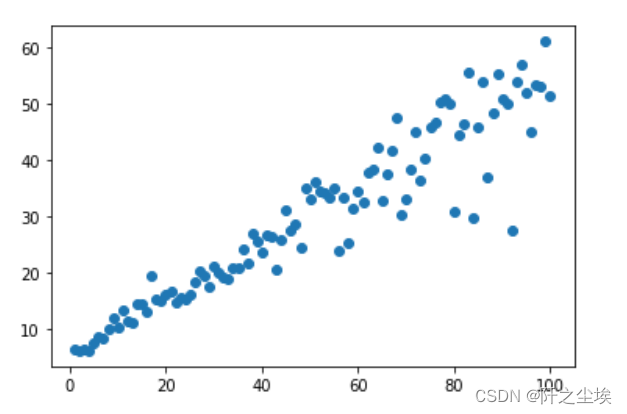

 可以看到X增大，Y的波动明显增大，数据存在异方差。

最小二乘

res_ols = sm.OLS(y, X).fit()
print(res_ols.summary())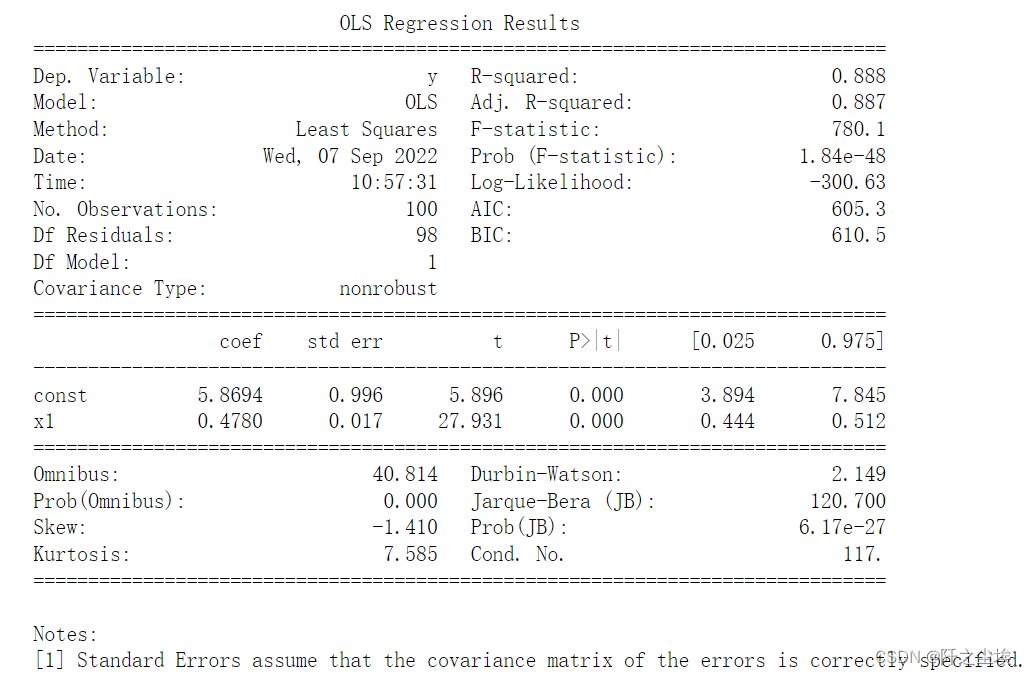

 可以看到拟合优度为88.8%。

加权最小二乘

将最小二乘的残差取出来，绝对值后，再倒数后最为wls的权重。

mod_wls = sm.WLS(y, X, weights=1.0 / abs(res_ols.resid))
res_wls = mod_wls.fit()
print(res_wls.summary())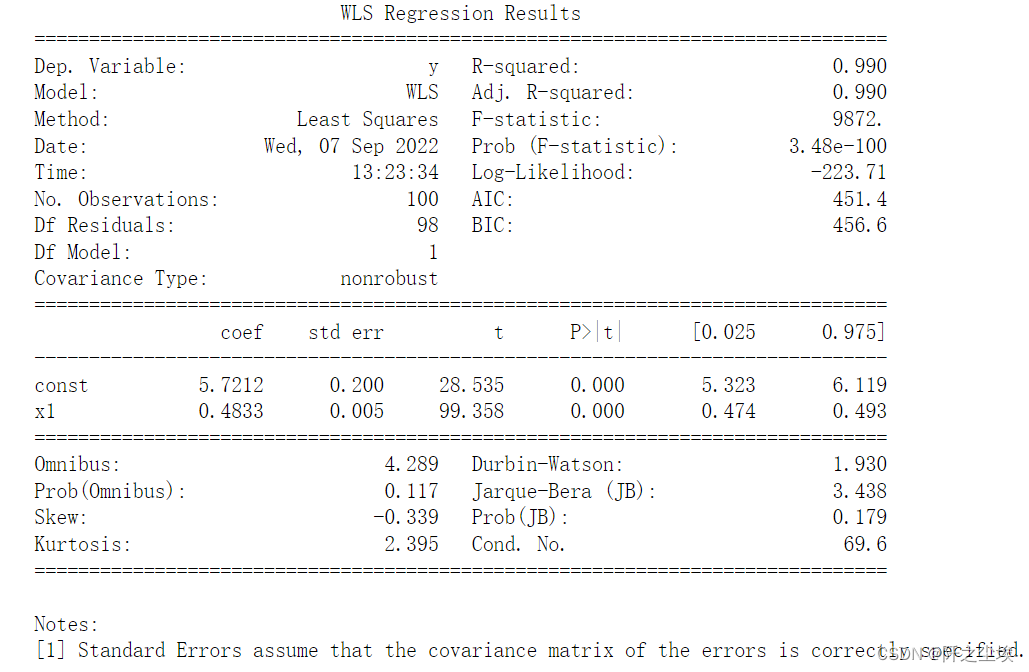

 

可以看到拟合优度变为了99% 

回归系数对比

print(res_ols.params)
print(res_wls.params)

 

 稍微比ols更加接近真实参数的值。

 画图对比

y_hat=res_wls.params[0]+res_wls.params[1]*x
y_hat_ols=res_ols.params[0]+res_ols.params[1]*x
plt.figure(figsize=(6,4))
plt.scatter(x,y)
plt.plot(x,y_hat,label='wls')
plt.plot(x,y_hat_ols,label='ols')
plt.legend()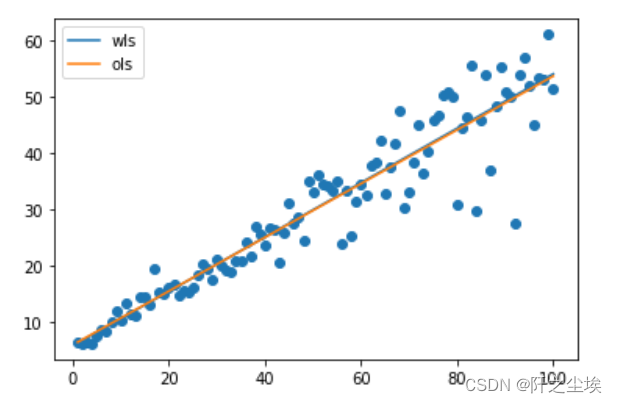

​​​​​​​

两条线有点重合.....在该数据集上可能效果不是很明显