阈值模型用于统计的几个不同区域,而不仅仅是时间序列。一般的想法是,当变量的值超过某个阈值时,过程可能表现不同。也就是说,当值大于阈值时,可以应用不同的模型,而不是当它们低于阈值时。例如,在药物毒理学应用中,可能低于阈值量的所有剂量都是安全的,而当剂量增加到阈值量以上时毒性增加。或者,在动物种群丰度研究中,种群可以缓慢增加至阈值大小,但是一旦种群超过一定大小,则可能迅速减少(由于有限的食物)。
阈值模型是制度转换模型(RSM)的特例。在RSM建模中,不同的模型适用于某些关键变量的不同值间隔。
单变量时间序列的阈值自回归模型(TAR)。在TAR模型中,AR模型在由因变量定义的两个或更多个值间隔中单独估计。这些AR模型可能是也可能不是相同的顺序。为方便起见,通常假设它们具有相同的顺序。
该文本仅考虑单个阈值,因此将存在两个单独的AR模型 - 一个用于超过阈值的值,另一个用于不超过阈值的值。困难在于确定是否需要TAR模型,使用的阈值以及AR模型的顺序。TAR模型可以工作的数据的一个特征是当值高于某个水平时,增加和/或减少的速率可能不同于当值低于该水平时。
阈值水平的估计或多或少是主观的。许多分析师探索了几种不同的阈值水平,试图提供良好的数据拟合(通过MSE值和残差的一般特征来衡量)。AR模型的顺序也可以是试错法,特别是当数据的固有模型可能不是AR时。一般来说,分析师从他们认为可能比必要的更高的订单开始,然后在必要时减少订单。
本文的第5.4节涵盖了阈值模型,并包含一个很好的例子。在本课中,我们将讨论该示例并提供R代码。这个例子的系列是美国流感死亡率每月11年(n = 132)。由于流感的流行性质,当比率超过某个阈值时,该系列的行为是非常不同的,而不是低于该值。
第一步绘制数据。以下是数据的时间序列图。
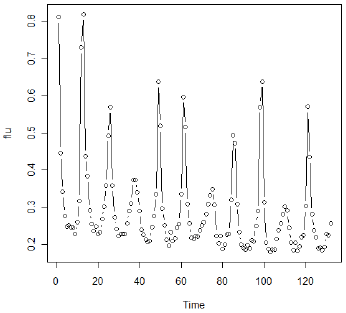
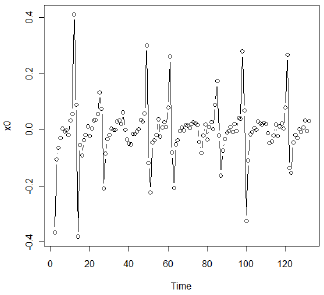
注意陡峭增加(和减少)的时期。作者还注意到略有下降趋势,因此首先考察了差异。以下是第一个差异的时间序列图。
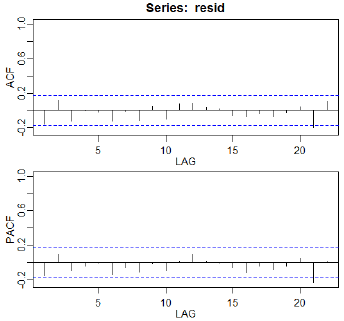
与原始数据一致,我们看到某些时期的急剧增加和减少。经过一些实验,作者决定对两个区域使用单独的AR(4)模型:第一个差异大于或等于0.05的数据和第一个差异小于0.05的数据。该模型非常适合,作为以下图表的证据 - 残差的ACF和PACF以及将实际的第一差异与预测的第一差异进行比较的图表。在比较实际值和预测值的图中,预测值沿着红色虚线。
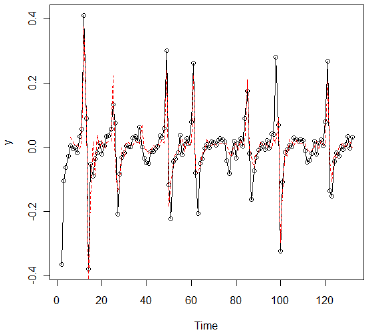
R代码示例
该示例的R代码如下。在ts.intersect 命令中,lag(,)命令创建滞后,输出的矩阵不包含缺少值的行。在代码中,我们对所有数据进行AR(4)模型的回归拟合,以便设置将在单独的制度回归中使用的变量。另请注意,阈值在命令c = .05中定义。 代码将执行两个回归,确定残差及其acf / pacf,并创建实际值和预测值的图。
flu = ts(flu)
plot(flu,type =“b”)
y = diff(flu,1)
plot(y,type =“b”)
x = model [ ,1]
##低于阈值的值的回归
less =(P [,1] <c)
x1 = x [less]
out1 = lm(x1~P1 [,1] + P1 [,2] + P1 [,3] + P1 [,4])
##回归值高于阈值
大=(P [, 1]> = c)
out2 = lm(x2~P2 [,1] + P2 [,2] + P2 [,3] + P2 [,4])
## Residuals
less [less == 1] = res1
##预测值
less =(P [,1 ] <c)
greater =(P [,1]> = c)
fit1 = predict(out1)
fit2 = predict(out2)
less [less == 1] = fit1
greater [greater == 1] = fit2 R中的tsDyn包将此代码简化为以下几个步骤:
flu.tar4.05 = setar(dflu,m = 4,thDelay = 0,th = .05)
通过拟合和诊断图显示上方和下方的最终模型.05 plot(flu.tar4.05)#cycles
如果我们没有为th选项提供阈值,则setar搜索网格以选择阈值(.036)

