SIR模型定义

SIR模型是一种传播模型，是信息传播过程的抽象描述。
SIR模型是传染病模型中最经典的模型，其中S表示易感者，I表示感染者，R表示移除者。

S：Susceptible，易感者
I：Infective，感染者
R：Removal，移除者

SIR模型的应用

SIR模型应用于信息传播的研究。

传播过程大致如下：最初，所有的节点都处于易感染状态。然后，部分节点接触到信息后，变成感染状态，这些感染状态的节点试着去感染其他易感染状态的节点，或者进入恢复状态。感染一个节点即传递信息或者对某事的态度。恢复状态，即免疫，处于恢复状态的节点不再参与信息的传播。

SIR的微分方程

a为感染率、b恢复率

注意：

t为某个时刻，例如t=1，S(1)为第一天易感人群的人数。
无论t为什么时刻，总人数是不变的，即N(t)=S(t)+I(t)+R(t)。
人口总数总保持一个常数，即N(t)=K，不考虑人口的出生、死亡、迁移等因素。

这里介绍一个使用R模拟网络扩散的例子。

第一步，生成网络。

规则网

1.  g =graph.tree(size, children =2); plot(g)
2.   

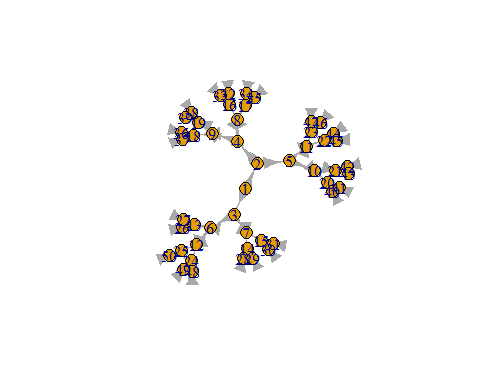
1.  g =graph.star(size); plot(g)
2.   

1.  g =graph.full(size); plot(g)
2.   

1.  g =graph.ring(size); plot(g)
2.   

第二步，随机选取一个或n个随机种子。 

1.  # initiate the diffusers
2.   
3.  seeds_num =1 diffusers =sample(V(g),seeds_num) ;
4.   
5.  diffusers
6.   
7.  ## + 1/50 vertex:
8.   
9.  ## [1] 43
10.   
11.  infected =list()
12.   
13.  infected[[1]]=diffusers#

第三步，传染能力

在这个简单的例子中，每个节点的传染能力是0.5，即与其相连的节点以0.5的概率被其感染,每个节点的回复能力是0.5，即其以0.5的概率被其回复。在R中的实现是通过抛硬币的方式来实现的。

1.  ## [1] 0
2.   

显然，这很容易扩展到更一般的情况，比如节点的平均感染能力是0.128，那么可以这么写： 节点的平均回复能力是0.1，那么可以这么写

1.  p =0.128
2.   
3.  coins =c(rep(1, p*1000), rep(0,(1-p)*1000))
4.   
5.  sample(coins, 1, replace=TRUE, prob=rep(1/n, n))
6.   
7.  ## [1] 0
8.   
9.  n =length(coins2)
10.   
11.  sample(coins2, 1, replace=TRUE, prob=rep(1/n, n))
12.   
13.  ## [1] 0

当然最重要的一步是要能按照“时间”更新网络节点被感染的信息。
 

1.  keep =unlist(lapply(nearest_neighbors[,2], toss))
2.   
3.  new_infected =as.numeric(as.character(nearest_neighbors[,1][keep >=1]))
4.   
5.  diffusers =unique(c(as.numeric(diffusers), new_infected))
6.   
7.  return(diffusers)}
8.   
9.  set.seed(1);

开启扩散过程！

先看看S曲线吧：

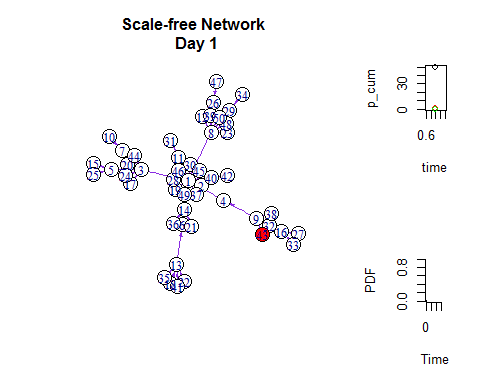
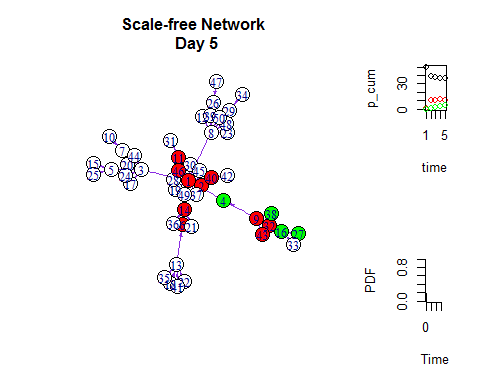
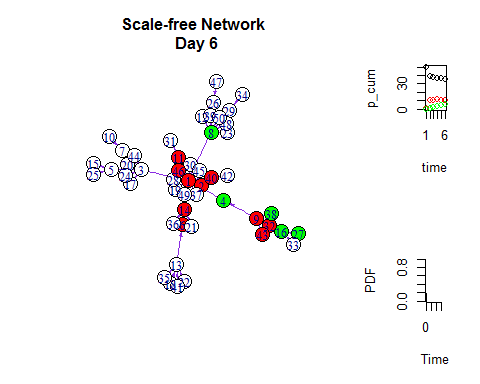
为了可视化这个扩散的过程，我们用红色来标记被感染者。

1.  # generate a palette#
2.   
3.  plot(g, layout =layout.old)
4.   
5.  set.seed(1)#
6.   
7.  library(animation)# start the plot
8.   
9.  m =1

如同在Netlogo里一样，我们可以把网络扩散与增长曲线同时展示出来：

1.  set.seed(1)
2.   
3.  # start the plot
4.   
5.  m =1
6.   
7.  p_cum=numeric(0)
8.   
9.  h_cum=numeric(0)
10.   
11.  i_cum=numeric(0)
12.   
13.  while( m<50 ) {# start the plot
14.   
15.  layout(matrix(c(1, 2, 1, 3), 2,2, byrow =TRUE), widths=c(3,1), heights=c(1, 1))
16.   
17.  V(g)$color = "white"
18.   
19.  V(g)$color[V(g)%in%infected[[m ]] ] = "red"
20.   
21.  V(g)$color[V(g)%in%health[[m ]]] = "green"
22.   
23.  if(m<=length(infected))
24.   
25.   
26.   
27.   
28.   
29.   
30.   
31.   
32.   
33.   
34.   
35.  plot(pp~time, type ="h", ylab ="PDF", xlab ="Time",xlim =c(0,i), ylim =c(0,1), frame.plot =FALSE)
36.   
37.  m =m +1
38.   
39.  }

 

---