并查集就是一个集合。这里需要用一个p[]数组来存储他的父节点，例如p[1] = 2，意思为1节点的父节点为2节点。这样就可以连接成一个集合。判断俩个元素是否在同一个集合中判断条件为：有共同的祖宗节点。

#include<iostream>
using namespace std;
const int N = 1e5 + 9;
int a, b, p[N], n, m;

int find(int x)//返回x的祖宗节点 + 路径压缩：让每个节点的父节点都为根节点
{
    //p[x] == x表示为根节点
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    //初始化，每个点开始的父节点都看作是自己
    for (int i = 1; i <= n; ++i) p[i] = i;
    while (m--)
    {
        char op;
        cin >> op >> a >> b;
        //让a的祖宗节点的父亲连接到b的祖宗节点上
        if (op == 'M') p[find(a)] = find(b);
        else
        {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

查找函数是并查集的核心，因为这里还加了一个路径压缩，第一次查找完后，就直接将他的父节点赋值为他所在集合的祖宗节点了。 

int find(int x)//返回x的祖宗节点 + 路径压缩：让每个节点的父节点都为根节点
{
    //p[x] == x表示为根节点
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

这里我画张图来演示。

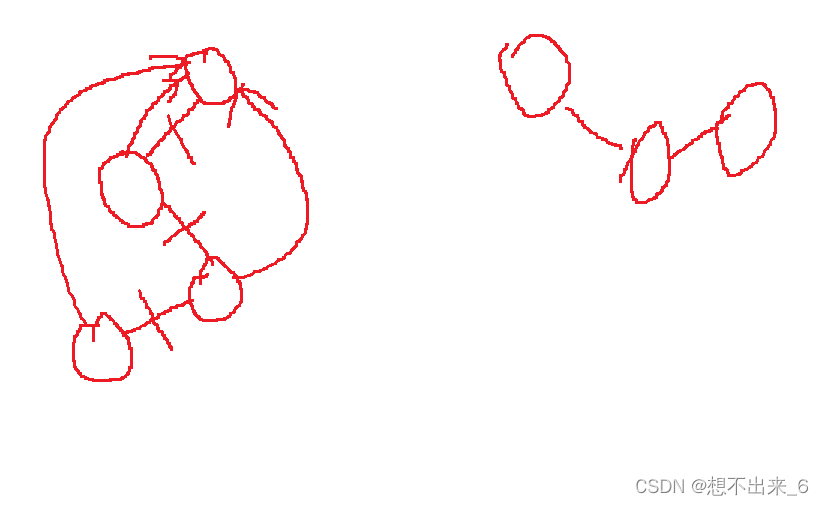
合并集合只需要将一个集合的祖宗节点连接到另一个集合的祖宗节点的下面。

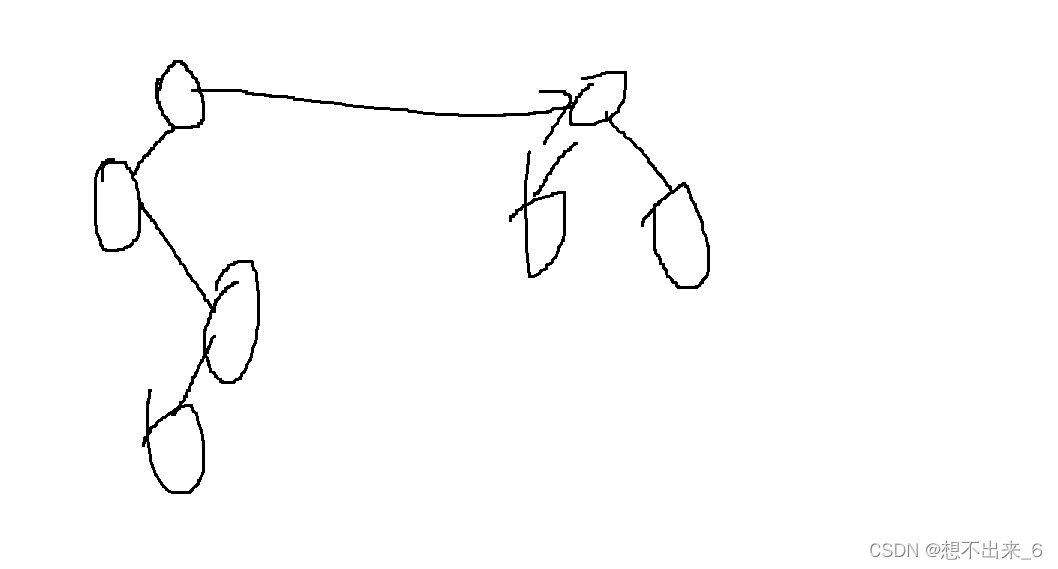
还有p[]数组一开始要初始化为自己，因为一开始所有节点都是祖宗节点。