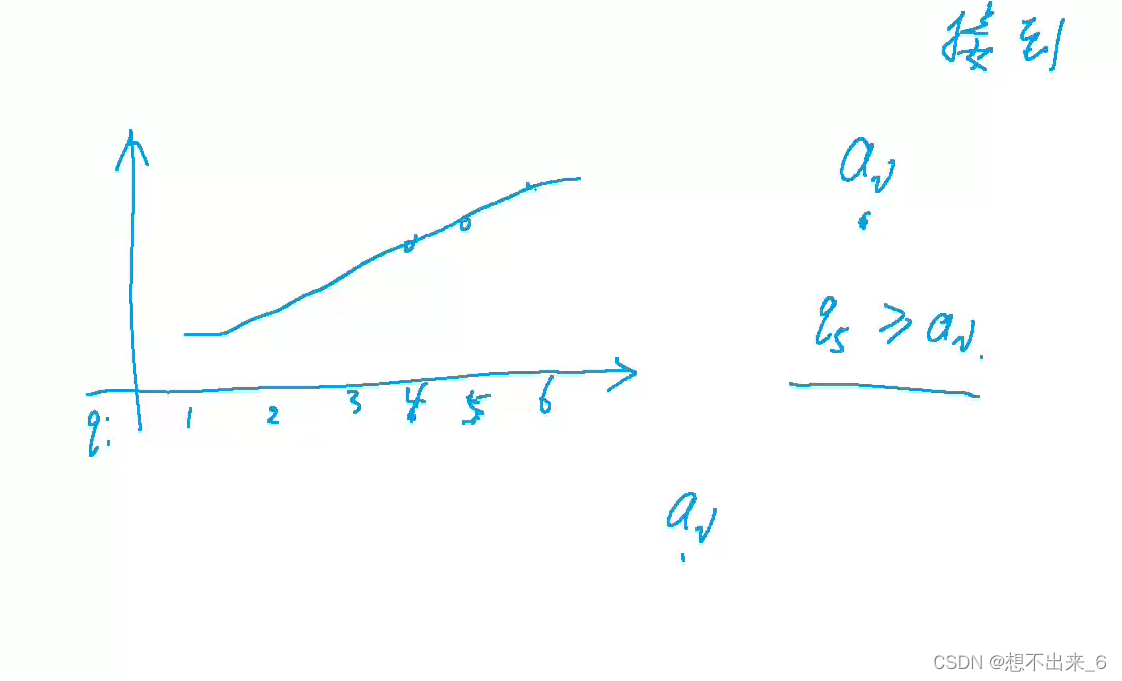
用二分的思想求最长上升子序列的思想就是保持单调性,用一个q[]数组来作为一个单调数组。
每次将a[i]放进q数组中,但是要保持单调性,q数组的长度就是答案。
q[]数组中存的是所以以下标为长度的最长子序列的结尾的最小值。
理解q[]数组的意义后那么就可以知道q数组下标从1开始有效。
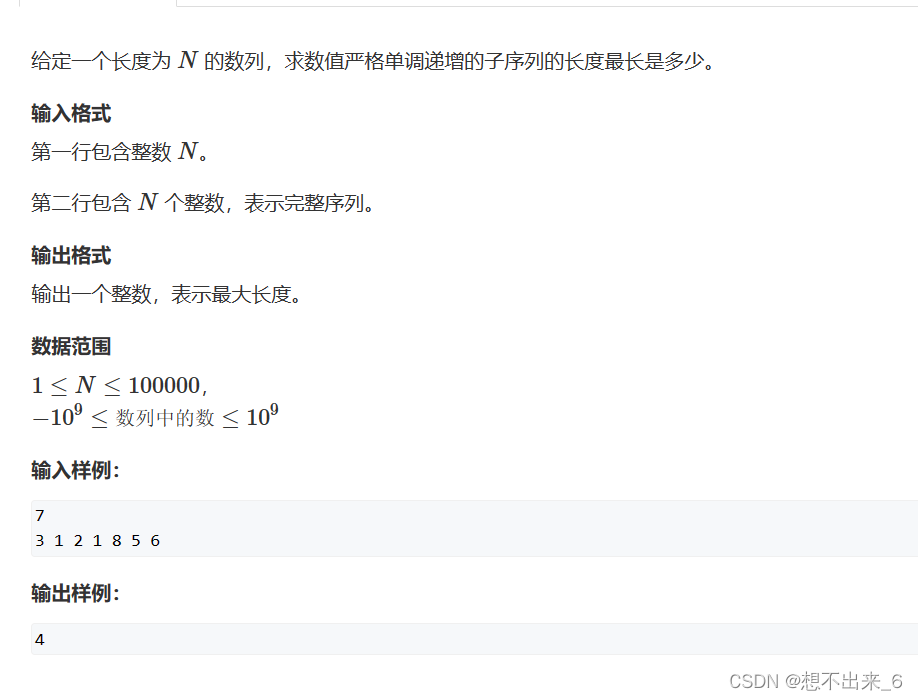
//二分 最大上升子序列
#include<iostream>
using namespace std;
const int N = 1e5 + 9;
int a[N], q[N], n;
//q[]是一个单调数组
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; ++i) cin >> a[i];
int len = 0;
q[0] = -2e9;//赋值为最小值,保证不会对结果有影响
for (int i = 0; i < n; ++i)
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] < a[i]) l = mid;//找到一个最大且小于a[i]的数
else r = mid - 1;
}
len = max(len, r + 1);//找到之后r + 1就是最大上升序列
q[r + 1] = a[i];//a[i]为q[]下一个数的最小的值,因为后面一个数必定大于等于a[i]
//所以需要更新他的值
}
cout << len;
return 0;
}根据上述代码举例,比如找到a[i]找的q[4]就是小于a[i]的最大的数,用因为q[]数组是单调的所以q[5]的值大于等于a[i],这时就可以更新q[5]了,因为q[5]比原先的值小,那么最长子序列的潜力就更大了。
至于二分寻找最大小于a[i]的位置。r先初始化为len的原因就显而易见了,因为就是在q[]数组中寻找嘛!r是找到的位置,r + 1就是应该的最长子序列长度。例如:q[4]为找到的最大小于a[i]的位置,q[r + 1]会被更新成a[i]所以求len时要用r + 1.

