字符串
字符串和列表是两种最常用的数据结构,所以相关的算法也很多,可谓是花样百出,防不胜防。反而是像栈,队列,树这些不常见的结构,套路更简单一些。
题目:
- 实现 strStr() 找到字符串的位置
- 最长公共前缀
- 最长回文子串
- 最长公共子串
- 全排列-无重复数字
- 全排列-含重复数字
- 数组子集
- 组合总和-数字无限次数
- 组合总和-数字使用一次
实现 strStr()
题目:
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll"
输出: 2
示例 2:
输入: haystack = "aaaaa", needle = "bba"
输出: -1
方法:该题目属于滑动窗口的范畴。
所谓滑动窗口:
一个窗口中包含长度为N的数据,逐步向下循环,不断生成新的窗口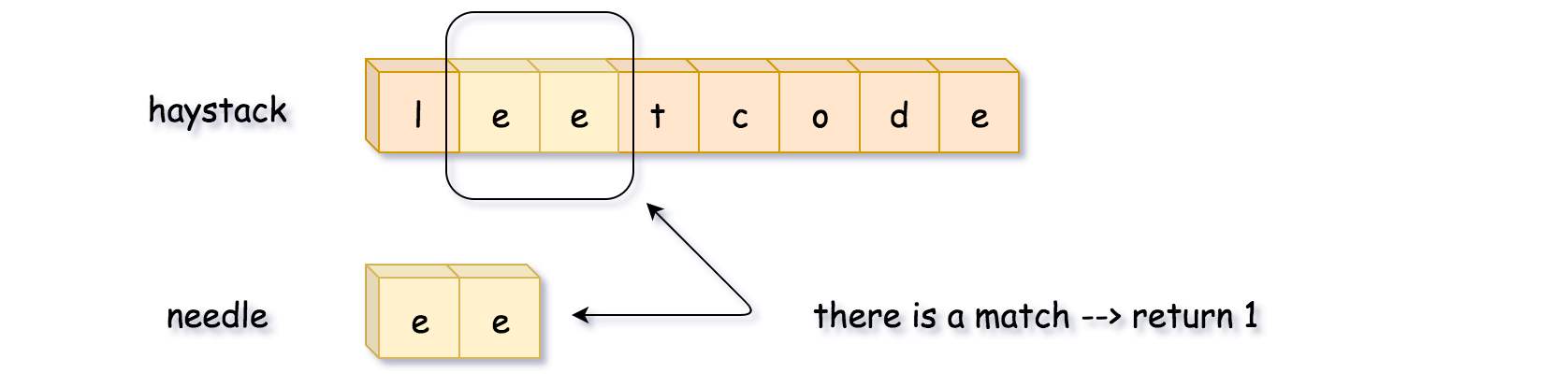
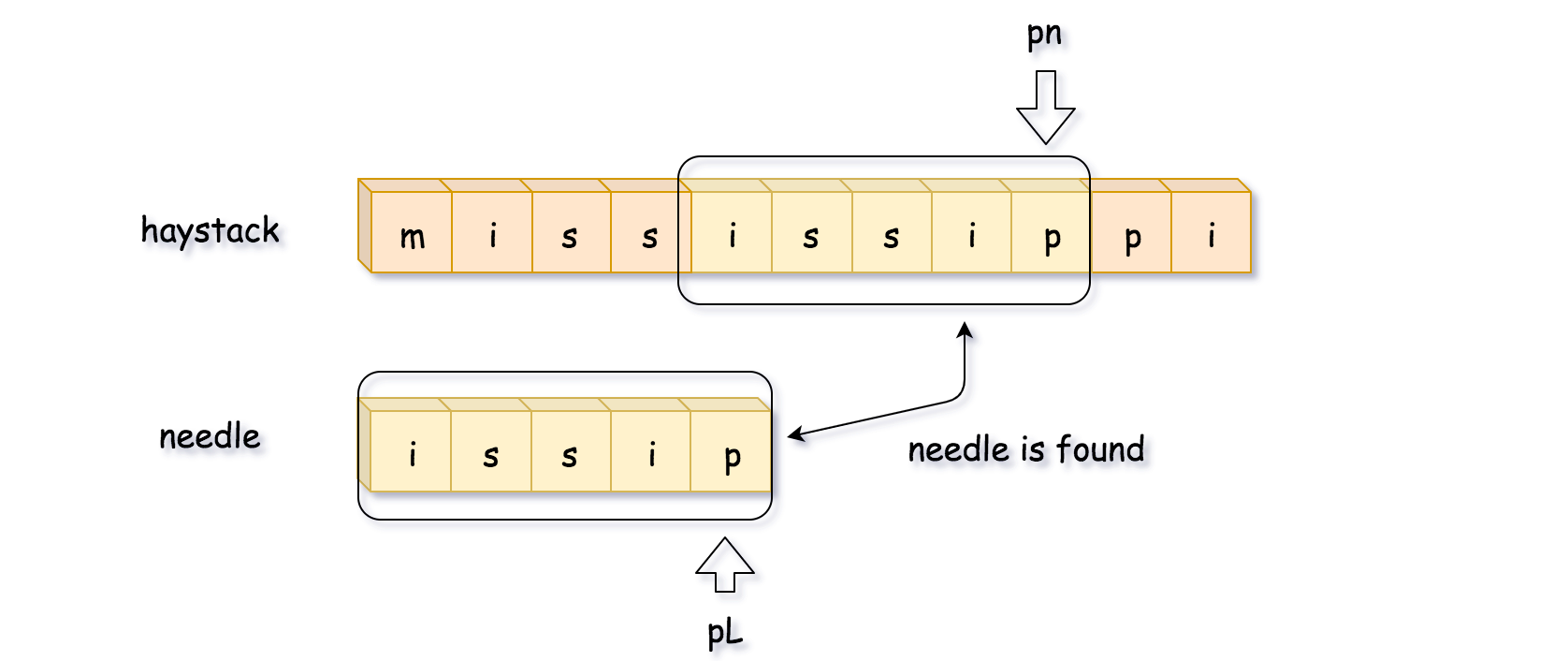
寻找子串有多种方法,包含:
- 循环长串,比较长串和子串的第一个数值,相同则与子串继续比下去,不同就比较下一位
- 对子串求哈希值,对父串相同长度的子串求哈希值,比较哈希值。是滑动串口的另一个比较方式。
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
if not needle:
return 0
if len(haystack) < len(needle):
return -1
for i in range(len(haystack)):
if haystack[i] == needle[0]:
if haystack[i:i+len(needle)] == needle:
return i
return -1
以上滑动窗口是静态变化的框口,还有一种是动态窗口。参见数组的长度最小的子数组。该题的思想就是一边向窗口中增加元素,如果元素的和大于某一个固定值时,在减少左边的窗口的值。这样的使用就是一个动态的窗口变化的过程。
最长公共前缀
寻找多个字符串的公共前缀有两种方式:
- 横向比较,先比较前两个,找到公共串,然后拿公共串去比较剩下的串
- 纵向比较,从0开始取出每个串的数值比较,相同继续,不相同退出。
- 进阶方法,只比较最长和最短的字符串即可
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
if len(strs) == 0:
return ""
# min函数巧用。指定比较条件。比较列表中长度,求最短长度的字符串
min_str = min(strs,key=lambda x:len(x))
for i in range(len(min_str)):
c = min_str[i]
for j in range(len(strs)):
if c != strs[j][i]:
return min_str[:i]
return min_str
特别收获
min使用方式
描述:
函数功能为取传入的多个参数中的最小值,或者传入的可迭代对象元素中的最小值。
语法:
min(iterable, *[, key, default])
min(arg1, arg2, *args[, key])
参数介绍:
默认数值型参数,取值小者;
字符型参数,取字母表排序靠前者。
key---可做为一个函数,用来指定取最小值的方法。
default---用来指定最小值不存在时返回的默认值。
arg1---字符型参数/数值型参数,默认数值型
最长回文子串
题目:
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
中心扩散法
遍历整个字符串,以每一个字符为中心,向两边扩散,如果两边相同则继续,能够找到最大的回文串
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n == 0:
return ""
res = s[0]
def extend(i, j, s):
while(i >= 0 and j < len(s) and s[i] == s[j]):
i -= 1
j += 1
return s[i + 1:j]
for i in range(n - 1):
e1 = extend(i, i, s)
e2 = extend(i, i + 1, s)
if max(len(e1), len(e2)) > len(res):
res = e1 if len(e1) > len(e2) else e2
return res
滑动窗口法
遍历整个字符串,取奇数数组和偶数数组。记录最大回文数。如果窗口内是回文,则增大回文数,扩大滑动窗口前后各一个,直到下一次比该滑动窗口更大的回文出现。中心扩散是每次都是当前字符扩散,而滑动窗口是在上一次的基础上直接扩散,避免了一层运算
# -*- coding:utf-8 -*-
class Solution:
def getLongestPalindrome(self, A, n):
max_len = 0
for i in range(n):
odd = A[i-max_len-1:i+1]
even = A[i-max_len:i+1]
if i-max_len-1 >=0 and odd == odd[::-1]:
max_len += 2
elif i-max_len >= 0 and even == even[::-1]:
max_len += 1
return max_len
最长公共子串
题目:
求两个字符串的公共子串:
bacefaebcdfabfaadebdaacabbdabcfffbdcebaabecefddfaceeebaeabebbad
dedcecfbbbecaffedcedbadadbbfaafcafdd
滑动窗口法:滑动窗口法和最长回文子串有异曲同工之妙。首先区分出长字符串和短字符串。遍历长字符串获得一个串,判断子串在不在短字符串中。如果在,子串向右增加一位,同时保证左边位不变。如果不在则以当前窗口的长度,继续向右滑动。
class Solution:
def LCS(self,str1 , str2 ):
# write code here
if len(str1) < len(str2):
str1, str2 = str2,str1
res = ''
max_len = 0
for i in range(len(str1)):
if str1[i - max_len : i+1] in str2:
res = str1[i-max_len : i+1]
max_len += 1
return res
动态规划
求两个字符串的公共子串,以两个字符串建立矩阵,如果在一条斜线上有连续的相同字符出现,则找出最大的斜线长度。
1ab2 3ab4
3 a b 4
1 0 0 0 0
a 0 1 0 0
b 0 0 1 0
2 0 0 0 0
就是找对角线为1最长的一条。建立二维dp矩阵。
当str1[i] == str2[j] 时,其长度就是对角线上一个+1 dp[i+1][j+1] = dp[i][j] + 1。
str1[1] != str2[j] 时,dp[i+1][j+1] = 0
class Solution:
def LCS(self,str1 , str2 ):
# write code here
n1 = len(str1)
n2 = len(str2)
dp = [ [0 for _ in range(n2+1)] for _ in range(n1+1)]
max_len = 0
for i in range(n1):
for j in range(n2):
if str1[i] == str2[j]:
dp[i+1][j+1] = dp[i][j] + 1
max_len = max(max_len, dp[i+1][j+1])
else:
dp[i+1][j+1] = 0
res = []
for i in range(n1):
for j in range(n2):
if dp[i+1][j+1] == max_len:
res = str1[i-max_len+1:i+1]
break
return res
全排列-无重复数字
题目:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
方法:很多种解法,其中有一种是交换思想。交换数组中数字的位置。
使用交换的深度搜索
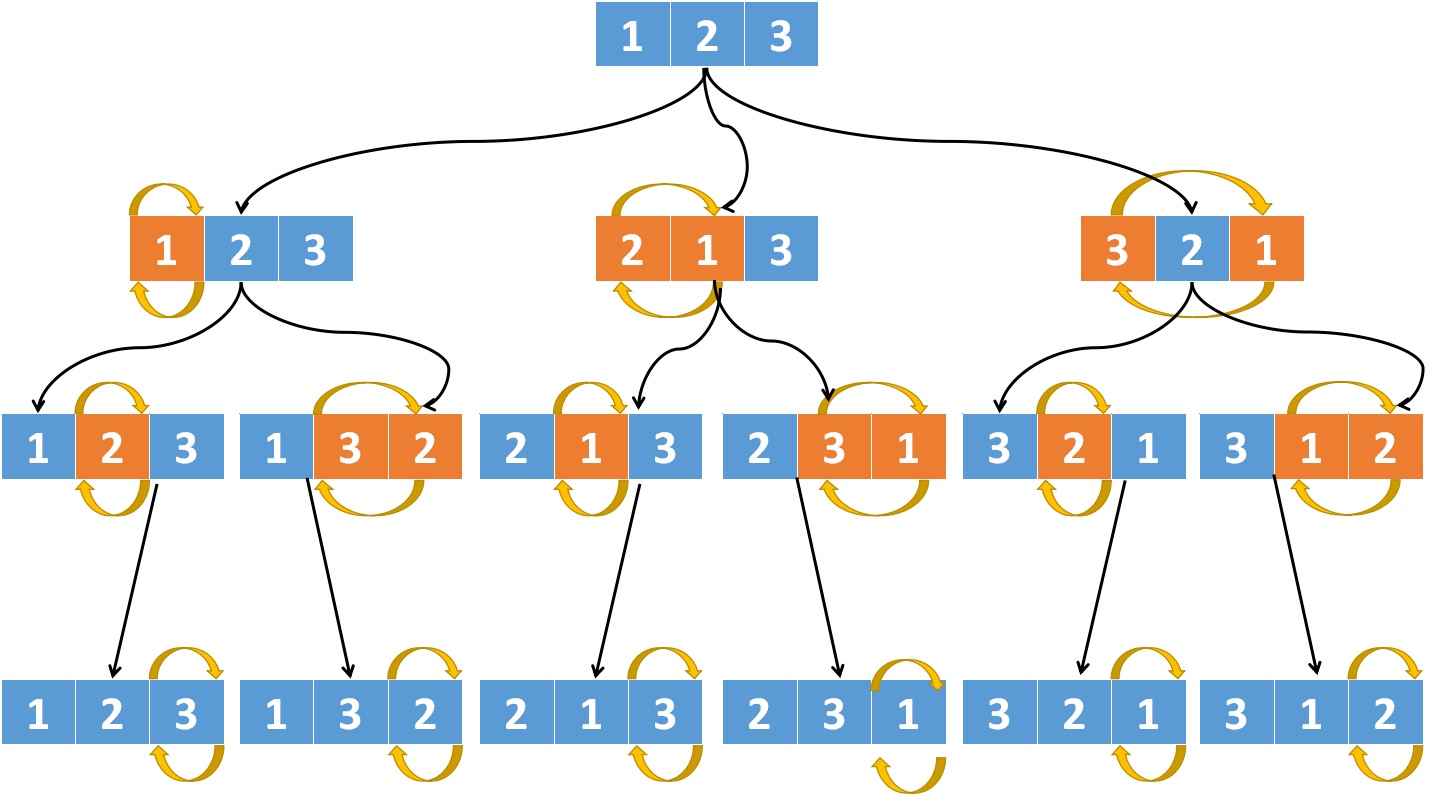
我们令index为0,指向数组的下标0
第一步,循环3次,对应上图中第二层,index指向0
i=index,交换i和index,此时1和1交换
i=index+1,交换i和index,此时1和2交换
i=index+3,交换i和index,此时1和3交换
第二步,循环两次,对应上图中第三层,index指向1
i=index,交换i和index,此时2和2交换
i=index+1,交换i和index,此时2和3交换
第三步,循环一次,对应上图中第三层,index指向2
i=index,交换i和index,此时3和3交换
知识点:回溯算法
def permute(string):
res = []
n = len(string)
def dfs(index):
if index == n:
res.append(list(string))
return
for i in range(index,n):
string[i],string[index] = string[index],string[i]
dfs(index+1)
string[i],string[index] = string[index],string[i]
dfs(0)
return res
string = [1,2,3]
res = permute(string)
print(res)
使用队列和栈完成的深度优先
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
import copy
if not nums:
return []
res = []
def dfs(queue,stack):
if not queue:
temp = copy.deepcopy(stack)
res.append(temp)
return
size = len(queue)
for i in range(size):
stack.append(queue.pop(0))
dfs(queue,stack)
queue.append(stack.pop())
dfs(nums,[])
return res
使用标记完成的深度优先
每次都遍历整个数组,在遍历时已经选择过的元素标记成已选择,完成保存后标记成未选择。
每次循环都循环3次,根据visited的标记选择是否加入。
当回退时,会存在这一次加入了最后一个,下一次调用加入了第二个。就是这样循序才使得排列组合能出来
第一层遍历分别是 1 2 3。
第二层就在第一层遍历剩余的元素里遍历如
第一层为1,nums=[1,2,3] visited=[1,0,0]
第二层为2, nums=[1,2,3] visited=[1,1,0]
第二层为3, nums=[1,2,3] visited=[1,1,1]
def permute(nums):
if not nums:
return
res = []
n = len(nums)
visited = [0] * n
def helper1(temp_list,length):
if length == n:
res.append(temp_list)
return
for i in range(n):
if visited[i] :
continue
visited[i] = 1
helper1(temp_list+[nums[i]], length+1)
visited[i] = 0
helper([], 0)
return res
string = [1,2,3]
res = permute(string)
print(res)
全排列-有重复数字
题目:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
来源:力扣(LeetCode)
链接:https:///problems/permutations-ii
方法:本题是全排列的一个进阶版本,全排列中是没有重复的,而本题是存在重复的数字。例如:[1,1,2]中: 1-,1,2和 1,1-,2 虽然元素位置不同,但是结果是一样的。这时就要在排列的时候去掉重复的元素。将当前元素和前面元素重复的,且前面元素没有被访问过的这一次情况去掉,称之为剪枝
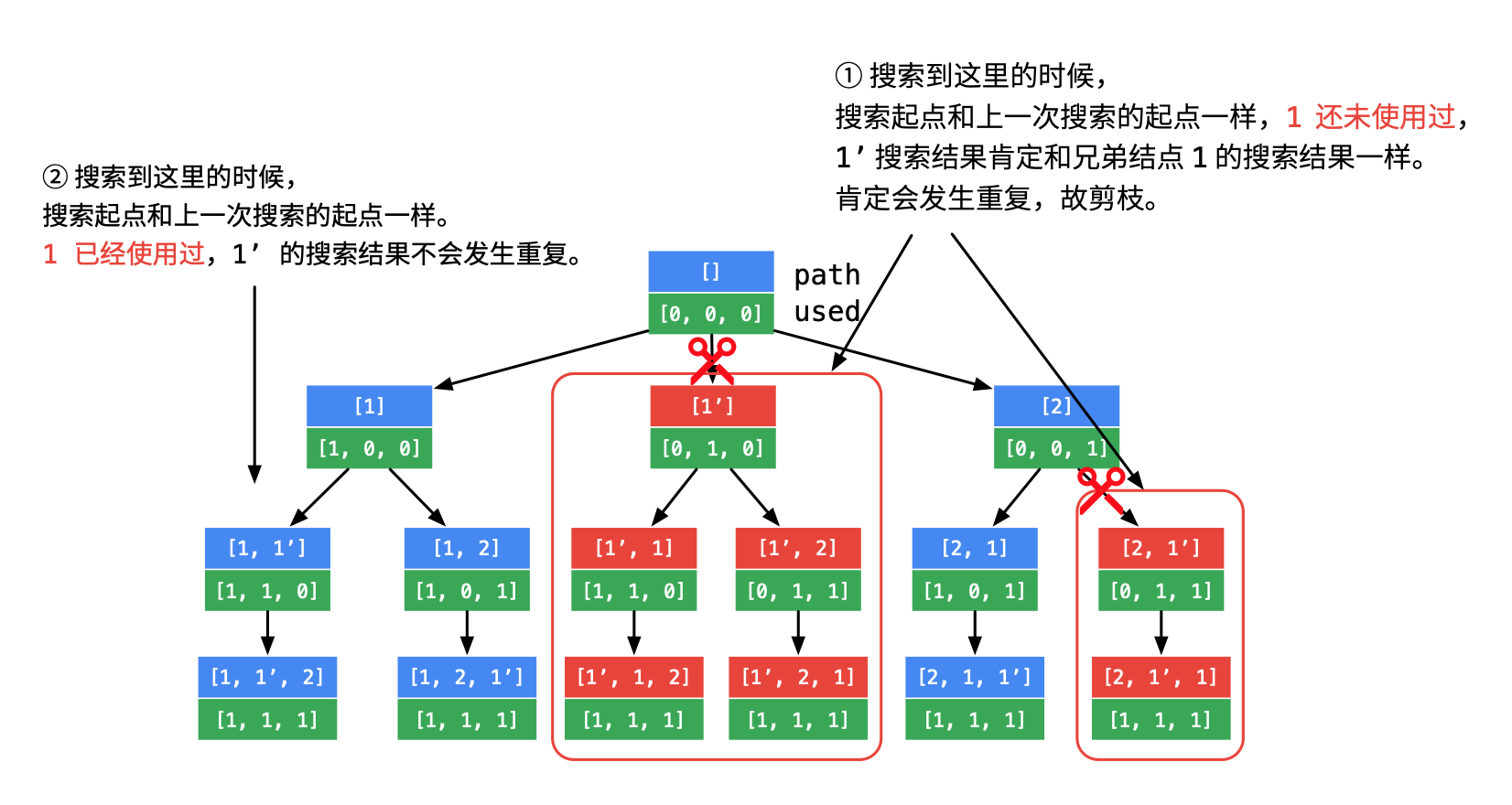
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
res = []
visited = [False] * n
# 需要先排列好,解决重复
nums.sort()
def dfs(temp, index):
if index == n:
res.append(temp)
return
for i in range(n):
# 剪枝的地方
if visited[i] or (i >0 and nums[i] == nums[i-1] and not visited[i-1]):
continue
visited[i] = True
dfs(temp+[nums[i]], index+1)
visited[i] = False
dfs([], 0)
return res
数组子集
题目:
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
解题思路:
顺序考虑,仅考虑选择的元素
除了上面的思路,还有一种需要遍历思考的思路,那就是顺序考虑,仅考虑选择的元素:
以空集[]开始,从第一个元素开始考虑,它有三种选择,1,2,3,组成[1],[2],[3]
当第一个元素为1的时候,第二个元素可以选择的是1后面的元素2,3,组成[1,2],[1,3]
当第二个元素为2的时候,此时[1,2],第三个元素可以选择3,组成[1,2,3]
当第一个元素为2的时候,第二个元素可以选择3,组成[2,3]
结束遍历,获得组成的8个答案,这说明了有效结果是没有条件的,任何结果都是有效的
def arrange(arr):
n = len(arr)
res = []
def dfs(temp_list, index):
res.append(temp_list)
for i in range(index, n):
dfs(temp_list+[arr[i]], i+1)
dfs([], 0)
print(res)
arr = [1,2,3]
arrange(arr)
>>>
[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
https:///problems/subsets/solution/hui-su-suan-fa-by-powcai-5/
https:///liweiwei1419/algo
组合总和-数字无限次数
题目:
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
来源:力扣(LeetCode)
链接:https:///problems/combination-sum
当我们遇到:“可行解是什么、可行解有多少个”这类问题时,最朴素的想法就是枚举,枚举出所有可能的结果,并在枚举的过程中不断删除不符合条件的解。
我们以问题39为例看看我们是怎么进行枚举的,以下图为例: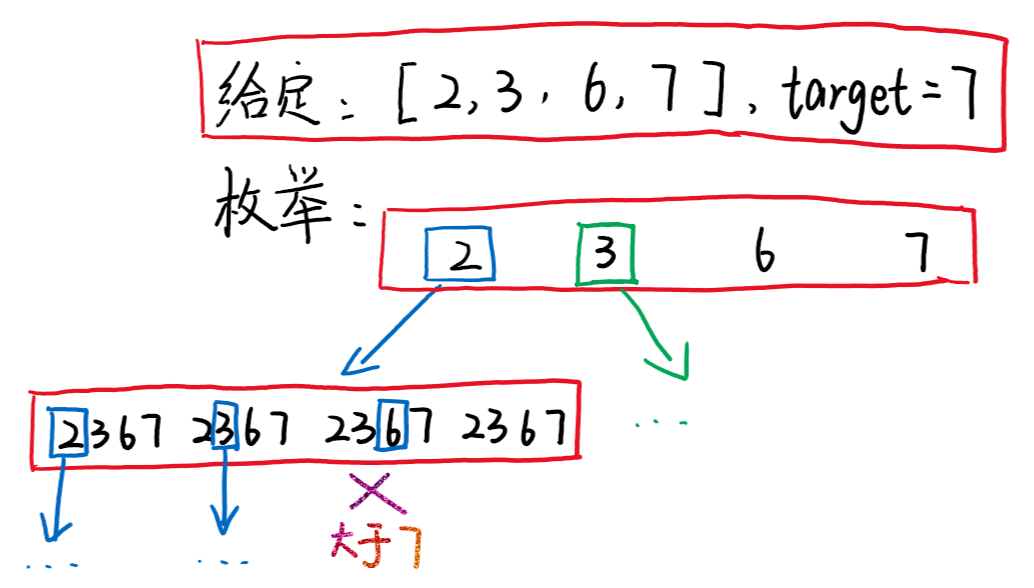
def arrange(arr, target):
n = len(arr)
res = []
def dfs(temp_list, index):
if sum(temp_list) == target:
res.append(temp_list)
return
if sum(temp_list) > target:
return
for i in range(index, n):
dfs(temp_list+[arr[i]], i)
dfs([], 0)
print(res)
arr = [2,3,4]
target = 7
arrange(arr, target)
组合总和-数字使用一次
题目:
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
链接:https:///problems/combination-sum/solution/hui-su-fa-yi-wen-jie-jue-si-dao-leetcodezu-he-zong/
来源:力扣(LeetCode)
方法:
该题的解法和组合总和之可重复元素的区别在于后者可以重复的使用元素,而前者不能重复使用元素。该题其实是和求数组的子数组问题非常类似,两者的思想是一致的。即:求出数组所有的子集,在子集中找出和为目标的子集。
def arrange(arr, target):
n = len(arr)
res = []
# 先排序,方便剔除重复项
arr.sort()
def dfs(temp_list, index):
if sum(temp_list) == target:
res.append(temp_list)
return
if sum(temp_list) > target or index == n:
return
for i in range(index, n):
if i>0 and arr[i] == arr[i-1]:
continue
dfs(temp_list+[arr[i]], i+1)
dfs([], 0)
print(res)
arr = [2,3,4,3]
target = 7
arrange(arr, target)
>>>>
[[3, 4]]
## 总结组合总和解题思路:
组合总和之元素可重复: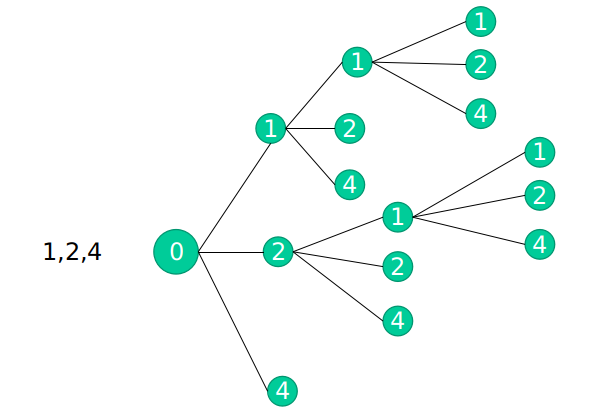
组合总和之元素不可重复: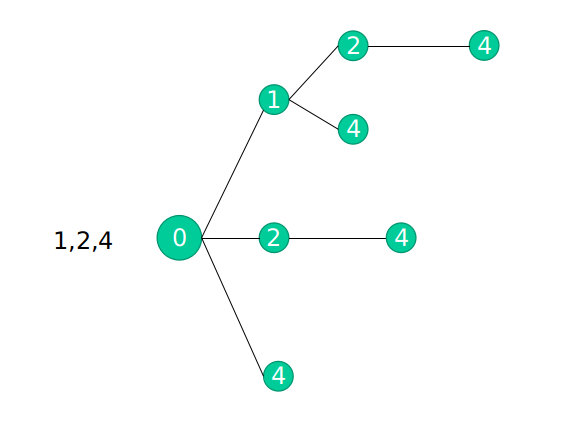
两者的访问模型如上图的差异,体现在代码上是:
def combinationSum(candidates,target):
n = len(candidates)
candidates.sort()
res = []
def dfs(index, total, arr):
for i in range(index, n):
# 差异点可重复就是能够访问数组中所有元素。
# 下一轮的运算也可以访问当前元素
dfs(i, total+candidates[i], arr+[candidates[i]])
dfs(0, 0, [])
return res
def combinationSum2(candidates, target):
candidates.sort()
res=[]
def backtrack(i,temp_sum,temp_list):
for j in range(i,len(candidates)):
if j>i and candidates[j]==candidates[j-1]:
continue
# 不可重复就是从当前元素的下一个元素访问,不可以访问当前元素
backtrack(j+1,temp_sum+candidates[j], temp_list+[candidates[j]])
backtrack(0,0,[])
return res
回溯算法
回溯有一个通用的模板,基本上可以套用到所有回溯的问题上,如下所示:
res = []
def backtrack(路径, 选择列表):
if 满足结束条件:
res.append(路径)
return
if 满足剪枝条件:
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
字符串小结
关于字符串的算法有很多,因为字符串和列表很类似,有很多算法是通用的。比如双指针,滑动窗口等。字符串的技巧有全排列,回文串,公共子串等。对于字符串需要把握的一点就是:字符串不支持修改,千万不要在原字符串上修改字符。
在众多算法中,全排列是最经典的,多次考试遇到全排列,特别注意排列之前把数据排个序,就因为忘记排序,错失了某为的面试,教训是惨痛的。

