列表
一维列表
- 删除排序数组中的重复项
- 移动非0元素到头部
- 盛最多水的容器
- 删除排序数组中的重复项
- 长度最小的子数组
- 无重复字符的最长子串
- 前缀和
- 三数之和
- 合并区间
二维列表
- 二维矩阵最大子矩阵和
- 旋转图像
- 杨辉三角
- 对角线遍历
- 矩阵元素查找
- 容器盛水
二维矩阵最大子矩阵和
题目:
[5,6,-3,8,-9,2],
[1,-12,20,0,-3,-5],
[0,-7,-3,6,7,-1]
在矩阵中找到和最大的子矩阵。
矩阵:长方形,非强制要求正方形
方法:二维矩阵的子矩阵中和最大的。首先要明确的是子矩阵是长方形而不是正方形。在二维矩阵中确定一个子矩阵的方法是确定矩阵的左上角和右下角。确定左上角就是确定x,y,使用两层for循环可以遍历到任意一个左上角。同理两层for循环也可以遍历到一个右下角。
暴力循环 两个for循环确定矩阵左上角;两个for循环确定矩阵右下角。两个for循环确定子矩阵和知识点: 二维列表的遍历
def func(matrix):
rows = len(matrix)
cols = len(matrix[0])
max_value = 0
for top in range(rows):
for left in range(cols):
for botton in range(top, rows):
for right in range(left, cols):
temp_list = []
for i in range(top, botton+1):
for j in range(left, right+1):
temp_list.append(matrix[i][j])
max_value = max(max_value, sum(temp_list))
# print(temp_list)
return max_value
matrix = [
[5,6,-3,8,-9,2],
[1,-12,20,0,-3,-5],
[0,-7,-3,6,7,-1]
]
# res = func(matrix)
# print(res)
方法: 暴力循环的方法时间复杂度简直吓人。在一维列表中有最大子列表的题目,那么将二维列表变成一维列表来处理是否可行呢?就是将多行压缩成一行,然后在一行中找最大子序列和。
首先将二维列表所有的子列表都找出来,结果如下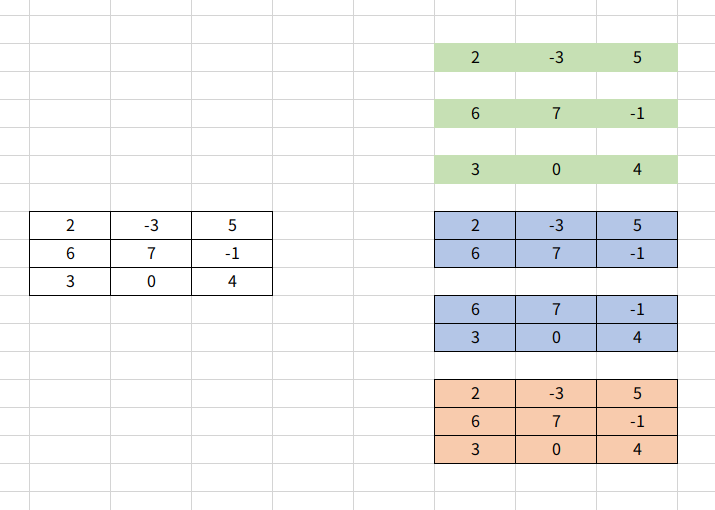
然后将二维子列表压缩成一维,这样一个一维列表就代表者二维子列表的和。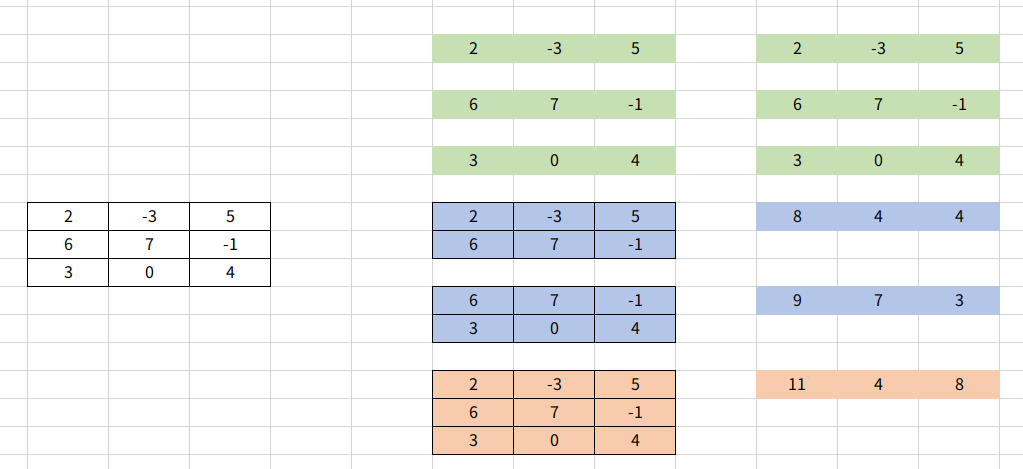
最后对所有一维列表求最大子序列和,结果即为二维列表的最大和子列表动态规划 将多行压缩成一行,对一维矩阵求最大值。3行的矩阵可以有6个行子矩阵
def max_sub_list(arr):
n = len(arr)
dp = [0] * n
dp[0] = arr[0]
for i in range(1, n):
if dp[i-1] + arr[i] > arr[i]:
dp[i] = dp[i-1] + arr[i]
else:
dp[i] = arr[i]
res = max(dp)
return res
def func2(matrix):
rows = len(matrix)
cols = len(matrix[0])
max_value = 0
for i in range(rows):
temp_list = [0] * cols
for j in range(i, rows):
for x in range(cols):
temp_list[x] += matrix[j][x]
res = max_sub_list(temp_list)
max_value = max(max_value, res)
return max_value
res = func2(matrix)
print(res)
旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
方法:有两种方法可解决矩阵旋转问题:
- 按照旋转规律,置换方格位置
- 先上下翻转,然后对角折叠
第一种方法:
由外层到内层,分别处理每一层。每一层中分别处理顶点到内部的位置。
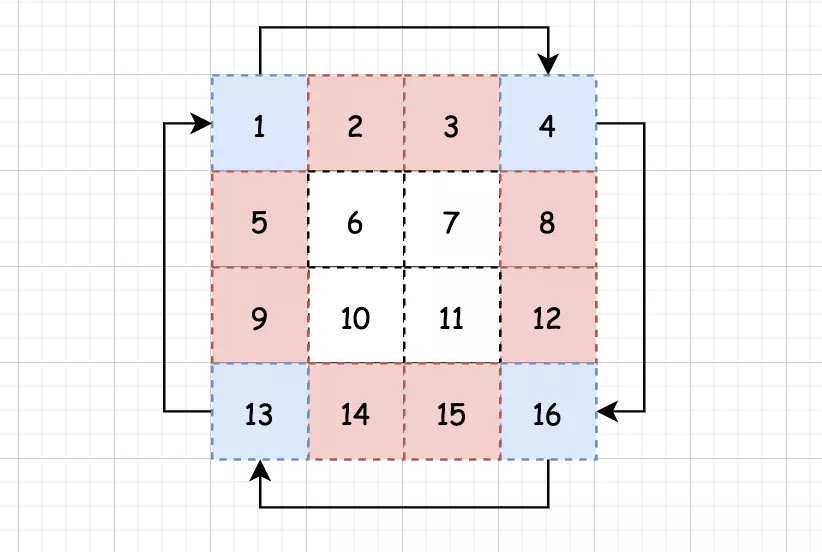
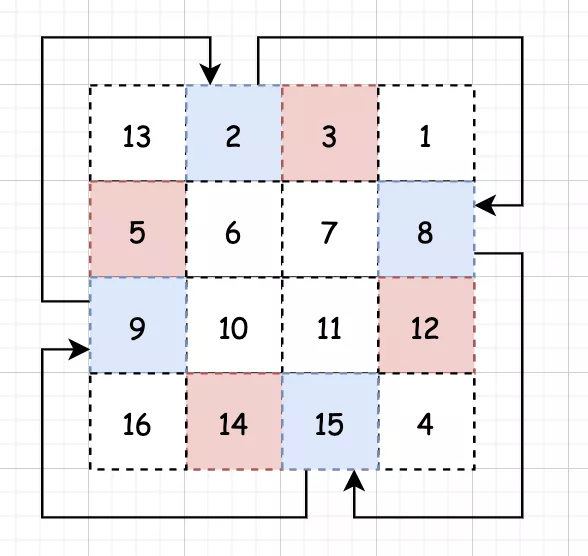
//java
class Solution {
public void rotate(int[][] matrix) {
int temp;
for (int x = 0, y = matrix[0].length - 1; x < y; x++, y--) {
for (int s = x, e = y; s < y; s++, e--) {
temp = matrix[x][s];
matrix[x][s] = matrix[e][x];
matrix[e][x] = matrix[y][e];
matrix[y][e] = matrix[s][y];
matrix[s][y] = temp;
};
};
}
}
第二种方法:
先上下翻转再对角线折叠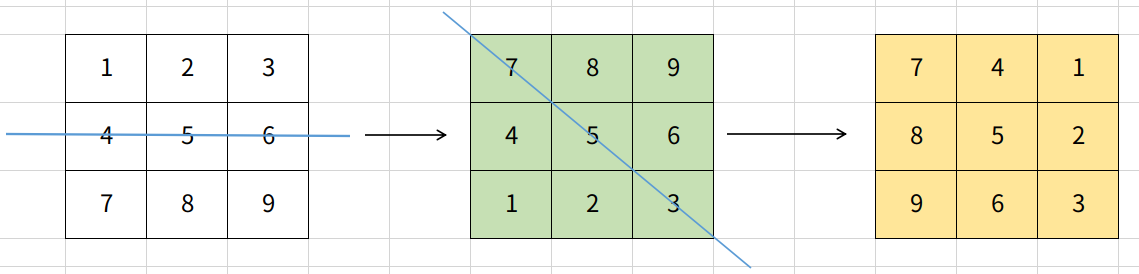
对角线遍历
题目:
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
![image_1el70dt1oudg14e6bnsg331ibn9.png-24kB][19]
方法:利用每一次输出的值坐标相加等于一个固定值这一个特征,将所有相同的坐标值放在一个字典中,判断是否翻转完成正确输出知识点: 二维列表的遍历
class Solution:
def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
group = collections.defaultdict(list)
for r,row in enumerate(matrix):
for c,num in enumerate(row):
sums = r + c
group[sums].append(num)
res = []
for k,s in group.items():
if k % 2 == 0:
s = s[::-1]
for p in s:
res.append(p)
return res
from collections import defaultdict
def output(arr):
temp_arr = defaultdict(list)
for i in range(len(arr)):
for j in range(len(arr[0])):
sums = i + j
temp_arr[sums].append(arr[i][j])
print(temp_arr)
res = []
for index,values in temp_arr.items():
if index % 2 == 0:
res.append(values[::-1])
else:
res.append(values)
print(res)
arr = [
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
output(arr)
def itor_fun(arr):
from collections import defaultdict
Dict = defaultdict(list)
for i in range(len(arr)):
for j in range(len(arr[0])):
Dict[i+j].append(arr[i][j])
print(Dict)
flag = False
for key, value in Dict.items():
if flag:
print(value)
else:
print(value[::-1])
flag = not flag
arr = [
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
itor_fun(arr)
矩阵元素查找
题目:
已知int一个有序矩阵mat,同时给定矩阵的大小n和m以及需要查找的元素x,且矩阵的行和列都是从小到大有序的。设计查找算法返回所查找元素的二元数组,代表该元素的行号和列号(均从零开始)。保证元素互异。
示例1
输入:
[[1,2,3],[4,5,6]],2,3,6
返回值:
[1,2]
方法:根据二维列表的特性,每一行都是从小到大,每一列都是从小到大。那么每一行的最后一个值肯定是最大的,判断targe与每一行最大的值,如果小于则肯定在下面,如果大于则在当前行。在当前行时向前遍历判断,值越来越小,如果存在肯定能找到。知识点:二维列表的遍历
class Solution:
def findElement(self, mat, n, m, x):
i = 0
j = m-1
while i < n and j >= 0:
if mat[i][j] == x:
return [i,j]
elif mat[i][j] > x:
j -= 1
else:
i += 1
return []
容器盛水
题目:
给定一个整形数组arr,已知其中所有的值都是非负的,将这个数组看作一个容器,请返回容器能装多少水。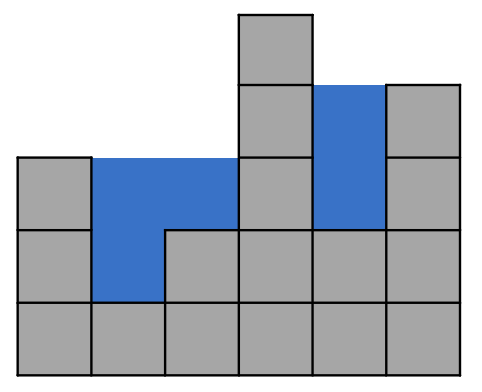
示例1
输入:
[3,1,2,5,2,4]
返回值:
5
示例2
输入:
[4,5,1,3,2]
返回值:
2
方法:找到每一个柱子的左边最大值和右边最大值,如果柱子的高度小于较小的那一个,就说明可以盛水。
本题可以使用的解法:
- 暴力,遍历每一个柱子,同时遍历得到柱子两边的最大值
- 动态规划,首先维护两个数组,每一个柱子左边最大值和右边最大值
- 先找到最高的柱子,然后从两边向最高的柱子进发
#
# max water
# @param arr int整型一维数组 the array
# @return long长整型
#
class Solution:
def maxWater(self , arr ):
n = len(arr)
left = [0] * n
for i in range(1,n):
left[i] = max(left[i-1], arr[i-1])
right = [0] * n
for i in range(n-2, -1, -1):
right[i] = max(right[i+1], arr[i+1])
# print(left)
# print(right)
res = 0
for i in range(n):
min_value = min(left[i], right[i])
if min_value > arr[i]:
res += min_value - arr[i]
# print(res)
return res
方法:先找到最大值,然后从两边向最大值靠近。在靠近的过程中,如果大于左边则没有盛水,如果小于左边则以左边为最小值来算盛水。
#
# max water
# @param arr int整型一维数组 the array
# @return long长整型
#
class Solution:
def maxWater(self , arr ):
max_value = max(arr)
res = 0
max_index = arr.index(max_value)
left = 0
right = 0
for i in range(max_index):
if arr[i] < left:
res += left - arr[i]
else:
left = arr[i]
for j in range(len(arr)-1, max_index, -1):
if arr[j] < right:
res += right - arr[j]
else:
right = arr[j]
return res
二维列表小结
对于二维列表的操作技巧有 化二维为一维,而遵循最基础操作的思想,总结二维列表的操作,那就是循环。普通循环:使用双层循环能够找到列表中任意一个元素。
arr = [
[10,22,68],
[41,23,66],
[28,88,84]
]
row = len(arr)
col = len(arr[0])
for x in range(row):
for y in range(col):
print(arr[x][y])
10
22
68
41
23
66
28
88
84
子矩阵:在二维列表中找出所有的子矩阵。在二维列表中确定一个左上角和一个右下角,就能确定一个子矩阵(包括一个点或多个点)。那么同时控制两个点就需要4层循环。
arr = [
[10,22,68],
[41,23,66],
[28,88,84]
]
row = len(arr)
col = len(arr[0])
for x in range(row):
for y in range(col):
for i in range(x,row):
for j in range(y, col):
print("左上角:{} -- 右下角:{}".format(arr[x][y], arr[i][j]))
左上角:10 -- 右下角:10
左上角:10 -- 右下角:22
左上角:10 -- 右下角:68
左上角:10 -- 右下角:41
左上角:10 -- 右下角:23
左上角:10 -- 右下角:66
左上角:10 -- 右下角:28
左上角:10 -- 右下角:88
左上角:10 -- 右下角:84
左上角:22 -- 右下角:22
左上角:22 -- 右下角:68
左上角:22 -- 右下角:23
左上角:22 -- 右下角:66
左上角:22 -- 右下角:88
左上角:22 -- 右下角:84
左上角:68 -- 右下角:68
左上角:68 -- 右下角:66
左上角:68 -- 右下角:84
左上角:41 -- 右下角:41
左上角:41 -- 右下角:23
左上角:41 -- 右下角:66
左上角:41 -- 右下角:28
左上角:41 -- 右下角:88
左上角:41 -- 右下角:84
左上角:23 -- 右下角:23
左上角:23 -- 右下角:66
左上角:23 -- 右下角:88
左上角:23 -- 右下角:84
左上角:66 -- 右下角:66
左上角:66 -- 右下角:84
左上角:28 -- 右下角:28
左上角:28 -- 右下角:88
左上角:28 -- 右下角:84
左上角:88 -- 右下角:88
左上角:88 -- 右下角:84
左上角:84 -- 右下角:84
单纯的二维列表并没有太多操作技巧,二维列表的更多操作是在动态规划中,能秀到眼花缭乱。

