解决⼀个回溯问题,实际上就是⼀个决
策树的遍历过程
。你只需要思考
3
个问题:
1、路径:也就是已经做出的选择。
2
、选择列表:也就是你当前可以做的选择。
3
、结束条件:也就是到达决策树底层,⽆法再做选择的条件。
回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满⾜结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核⼼就是 for
循环⾥⾯的递归,在递归调⽤之前「做选择」,在递归调⽤
之后「撤销选择」
,特别简单。
可以把「路径」和「选择」列表作为决策树上每个节点的属性
,⽐如下图列出了⼏个节点的属性:
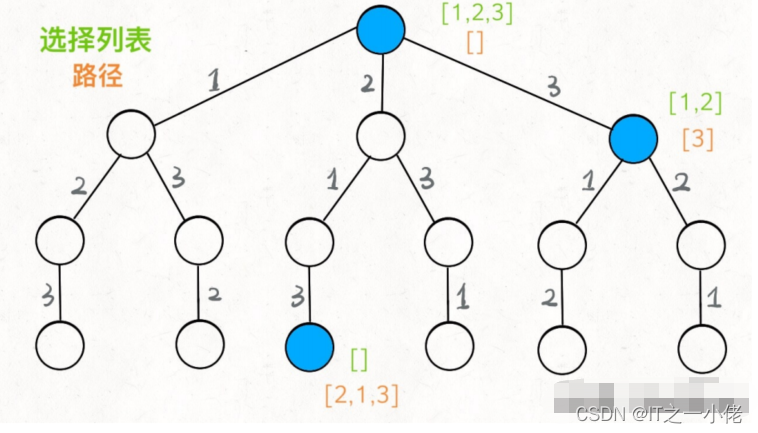
我们定义的 backtrack
函数其实就像⼀个指针,在这棵树上游⾛,同时要
正确维护每个节点的属性,每当⾛到树的底层,其「路径」就是⼀个全排
列
。
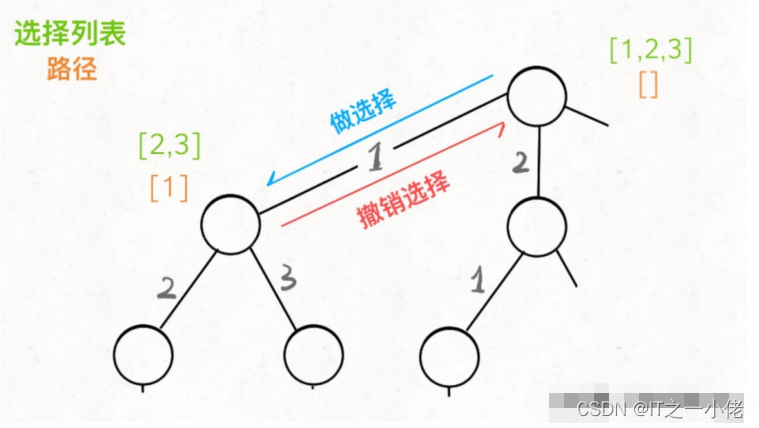
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加⼊选择列表
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置做⼀些操作,算法框架如下:
def backtrack(...):
for 选择 in 选择列表:
做选择
backtrack(...)
撤销选择
写 backtrack
函数时,需要维护⾛过的「路径」和当前可以做的「选择列
表」,当触发「结束条件」时,将「路径」记⼊结果集
。
⼀、全排列问题
详见博文:
数组全排列_IT之一小佬的博客-CSDN博客
示例代码:
class Solution(object):
def permute(self, nums):
n = len(nums)
ret, path = [], []
def backtrace():
if len(path) == n:
ret.append(path[:])
return
for i in range(n):
if nums[i] in path:
continue
path.append(nums[i])
backtrace()
path.pop()
backtrace()
return ret
nums = [1, 2, 3]
obj = Solution()
ret = obj.permute(nums)
print(ret)
⼆、
N
皇后问题
详见博文:
N 皇后问题_IT之一小佬的博客-CSDN博客
示例代码:
class Solution(object):
def solveNQueens(self, n):
def generate_board():
board = []
for i in range(n):
row[queens[i]] = "Q"
board.append("".join(row))
row[queens[i]] = "."
return board
def backtrack(row):
if row == n:
board = generate_board()
ret.append(board)
else:
for i in range(n):
if i in columns or row - i in diagonal1 or row + i in diagonal2:
continue
queens[row] = i
columns.add(i)
diagonal1.add(row - i)
diagonal2.add(row + i)
backtrack(row + 1)
columns.remove(i)
diagonal1.remove(row - i)
diagonal2.remove(row + i)
ret = []
queens = [-1] * n
row = ["."] * n
columns, diagonal1, diagonal2 = set(), set(), set()
backtrack(0)
return ret
obj = Solution()
ans = obj.solveNQueens(4)
print(ans)

