树
树也是一种常见的数据结构,比如电脑系统的文件资源管理器,如下图就是树形结构:

在数据结构中,树是若干结点的集合,是由唯一的根和若干棵互不相交的子树组成的,而每棵子树又是一棵树。
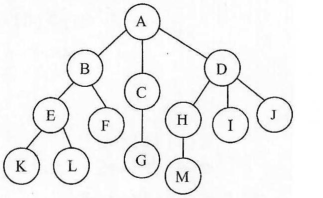
树的常见概念:
- 结点:A、B、C、D等都是结点,结点不仅包含数据元素,而且包含指向子树的指针。其中A是根结点,只有唯一一个。
- 叶子结点:又称为终端结点,没有孩子的结点,如K、L、F、G、M等都是叶子结点。
- 孩子结点:结点的子树的根,如A结点的孩子结点为B、C、D。
- 双亲结点:与孩子结点的定义对应,如B、C、D结点的双亲就是A结点。
- 兄弟结点:同一个双亲的孩子之间互为兄弟,如B、C、D三个结点互为兄弟。
- 结点的度:结点拥有的子树个数或者分支的个数。例如,A结点有3棵子树,所以A结点的度为3。
- 树的度:树中各结点度的最大值。如例子中结点度最大为3 (A、D结点)。
对于树知道上面简单的就差不多了,毕竟介绍树只是为了引出二叉树,进而引出红黑树。
树的存储结构有顺序存储和链式存储两种,这里不说明。
二叉树
二叉树是树的一种特殊形式,顾名思义,只有两个叉。
二叉树的定义:
- 每个结点最多只有两颗子树,注意,最多只有2个,可能是2个,可能是1个,也可能没有。
- 子树有左右顺序之分,不能颠倒。
二叉树有5种基本的形态:
- 空二叉树
- 只有根结点
- 只有左子树,右子树为空
- 只有右子树,左子树为空
- 既有左子树,又有右子树

二叉树又有两种特殊形式:满二叉树和完全二叉树。
满二叉树:一个二叉树的所有非叶子结点都存在左右孩子,并且所有叶子结点都在同一层上,那么这棵树称为满二叉树。

完全二叉树:对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个
二叉树为完全二叉树。


说明:通俗地说,一棵完全二叉树一定是由一棵满二叉树从右至左从下至上,挨个删除结点所得到的。如果跳着删除,则得到的不是完全二叉树。

二叉树的存储结构:链式存储和顺序存储。
- 顺序存储
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。
为什么这样设计呢?因为这样可以更方便地在数组中定位二叉树的孩子节点和父节点。

假设一个父节点的下标是parent,那么它的左孩子节点下标就是2×parent +1;右孩子节点下标就是2×parent + 2。
反过来,假设一个左孩子节点的下标是leftChild,那么它的父节点下标就是(leftChild-1)/ 2。
显然,对于一个稀疏的二叉树来说,用数组表示法是非常浪费空间的。

- 链式存储
链式存储是二叉树最直观的存储方式。

二叉树的结点最多可以指向左右两个孩子结点,所以二叉树的每一个结点包含3部分:存储数据的data变量、指向左孩子的left指针、指向右孩子的right指针。

