问：支持向量机是基于经验风险最小化(ERM) 原则构建的，因此有更好的泛化性能。

答：错误。支持向量机是一种基于结构风险最小化原则构建的机器学习算法，它可以通过寻找合适的分割超平面来实现分类任务，并且具有较好的泛化性能。

支持向量机基本原理与思想

支持向量机

SVM即支持向量机（Support Vector Machine），是有监督学习算法的一种，用于解决数据挖掘或模式 识别领域中数据分类问题。支持向量机是一种基于结构风险最小化原则构建的机器学习算法，它可以通过寻找合适的分割超平面来实现分类任务，并且具有较好的泛化性能。

基本原理

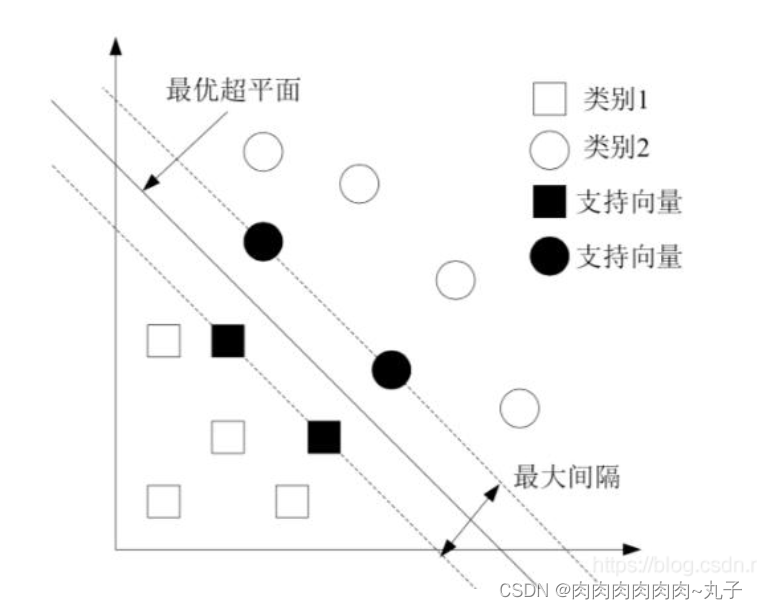
SVM算法 即寻找一个分类器使得超平面和最近的数据点之间的分类边缘（超平面和最近的数据点之间的 间隔被称为分类边缘）最大，对于SVM算法通常认为分类边缘越大，平面越优，通常定义具有“最大间隔”的决策面就是 SVM 要寻找的最优解。并且最优解对应两侧虚线要穿过的样本点，称为“支持向量”。其处理的基本思路为：把问题转化为一个凸二次规划 问题，可以用运筹学有关思想进行求解：
（1）目标函数
在线性SVM算法中，目标函数显然就是那个"分类间隔"，使分类间隔最大。
（2）约束条件
即决策面，通常需要满足三个条件：
1）确定决策面使其正确分类。
2）决策面在间隔区域的中轴线。
3）如何确定支持向量因此求解SVM问题即转化为求解凸二次规划的最优化问题。

支持向量机：就是用来分割数据点那个分割面，他的位置是由支持向量确定的(如果支持 向量发生了变化，往往分割面的位置也会随之改变), 因此这个面就是一个支持向量确定的 分类器即支持向量机。

线性可分数据的二值分类机理：系统随机产生一个超平面并移动它，直到训练集中属于不同类别的样本点正好位于该超平面的两侧。显然，这种机理能够解决线性分类问题，但不能够保证产生的超平面是最优的。支持向量机建立的分类超平面能够在保证分类精度的同时， 使超平面两侧的空白区域最大化，从而实现对线性可分问题的最优分类。
SVM的主要思想是：建立一个最优决策超平面，使得该平面两侧距平面最近的两类样 本之间的距离最大化，从而对分类问题提供良好的泛化力（推广能力）。