插入排序算法原理
插入排序算法类似于打扑克牌,每次从待排序区域抽出一张牌,然后通过比较插入到已排序区的合适的位置
插入排序算法动画演示
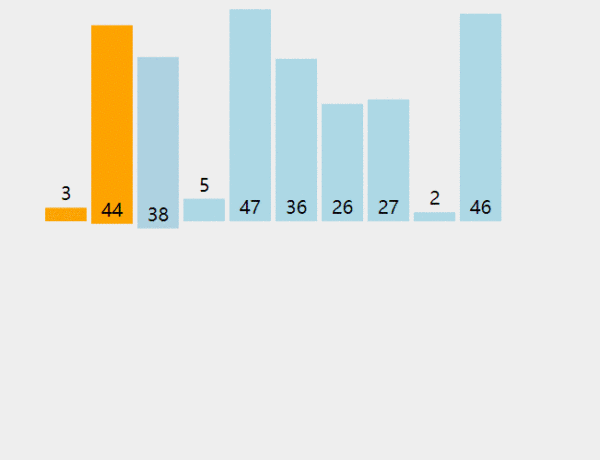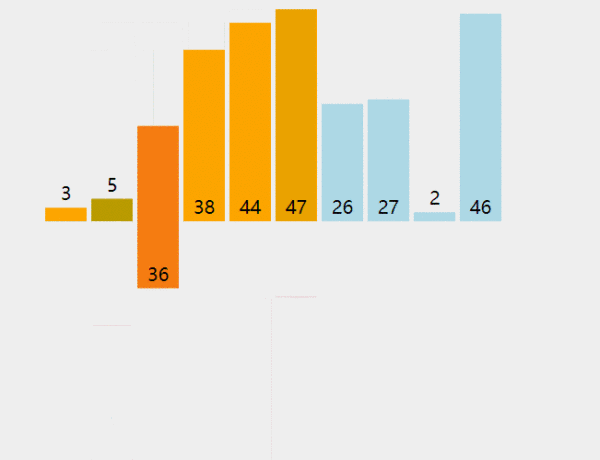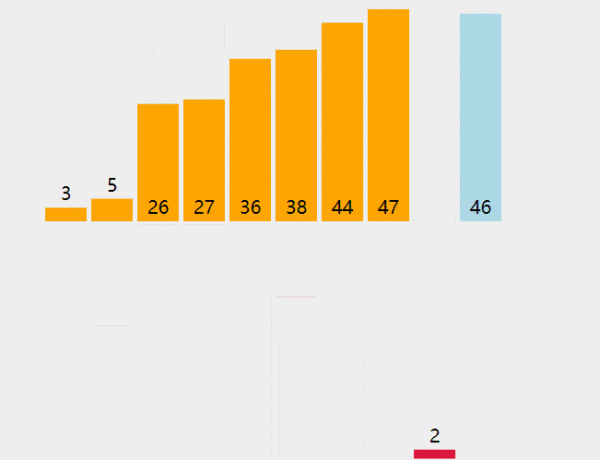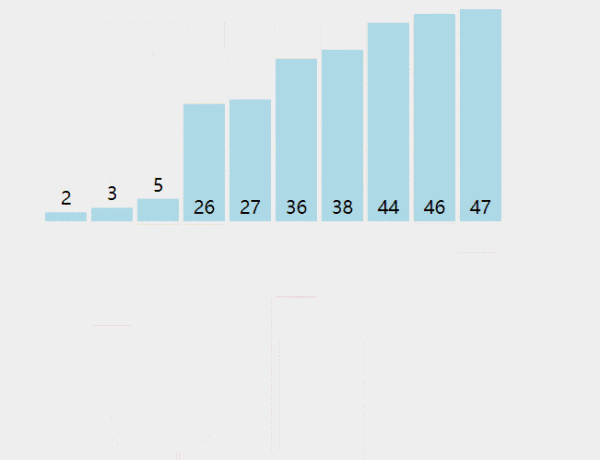
插入排序算法复杂度
通过分析插入排序算法,可以很容易发现插入排序算法的时间复杂度同样是n2
插入排序算法代码实现
代码如下:
def insert_sort(li):
for i in range(1,len(li)):
for j in range(i,0,-1):
if li[j]<li[j-1]:
li[j],li[j-1]=li[j-1],li[j]
else:
break
print(f"经过第{i}趟排序列表结果:{li}")
return li
if __name__=="__main__":
li=[9,1,6,3,4,8,7,0,2,5]
print(f"排序前列表:{li}")
li=insert_sort(li)
print(f"排序后列表:{li}")
执行结果如下:
排序前列表:[9, 1, 6, 3, 4, 8, 7, 0, 2, 5]
经过第1趟排序列表结果:[1, 9, 6, 3, 4, 8, 7, 0, 2, 5]
经过第2趟排序列表结果:[1, 6, 9, 3, 4, 8, 7, 0, 2, 5]
经过第3趟排序列表结果:[1, 3, 6, 9, 4, 8, 7, 0, 2, 5]
经过第4趟排序列表结果:[1, 3, 4, 6, 9, 8, 7, 0, 2, 5]
经过第5趟排序列表结果:[1, 3, 4, 6, 8, 9, 7, 0, 2, 5]
经过第6趟排序列表结果:[1, 3, 4, 6, 7, 8, 9, 0, 2, 5]
经过第7趟排序列表结果:[0, 1, 3, 4, 6, 7, 8, 9, 2, 5]
经过第8趟排序列表结果:[0, 1, 2, 3, 4, 6, 7, 8, 9, 5]
经过第9趟排序列表结果:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
排序后列表:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

