递归简介

• 递归的两个特点：调用自身和结束条件

如：

def func(x):
    if x>0:
        print(x)
        func(x-1)

func(3)

执行结果如下：

3
2
1

这里需要注意一下，如将打印语句放到下面，如下代码，结果将是完全不一样的

def func(x):
    if x>0:
        func(x-1)
        print(x)

func(3)

执行结果如下：

1
2
3

2、汉诺塔问题

• 汉诺塔问题：
  

• 当n=2时操作步骤：
  原始状况如下，目标是将A上的两个都移动到C上
  
  步骤一：将A上的小盘从A移动到B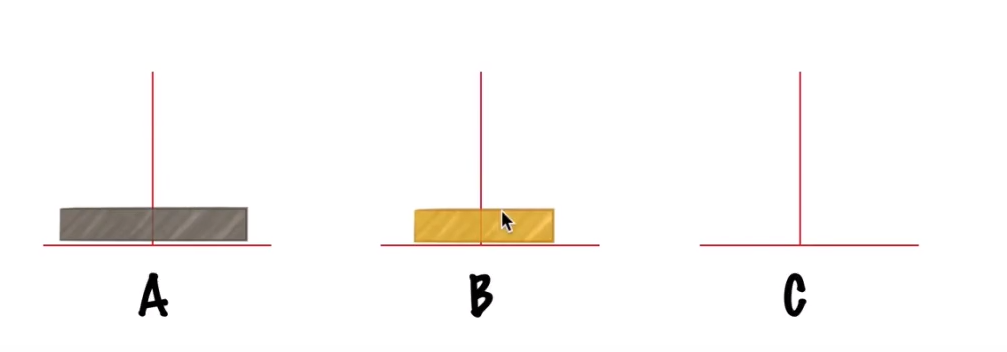
  
  步骤二：将A盘上的大盘移动到C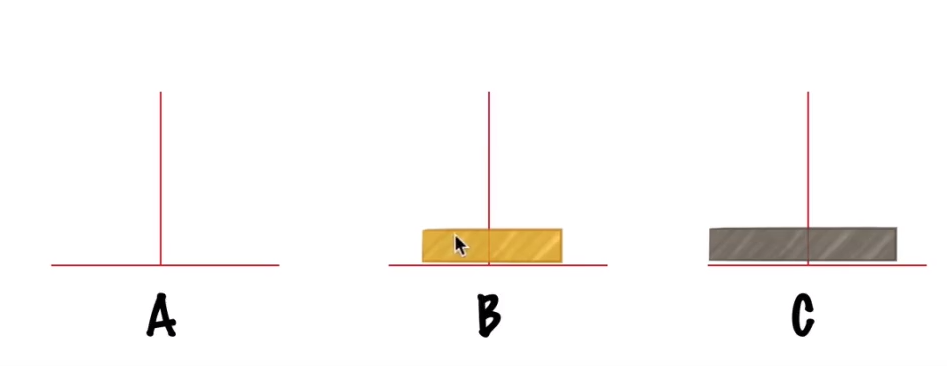
  
  步骤三：将B上的小盘移动到C，结束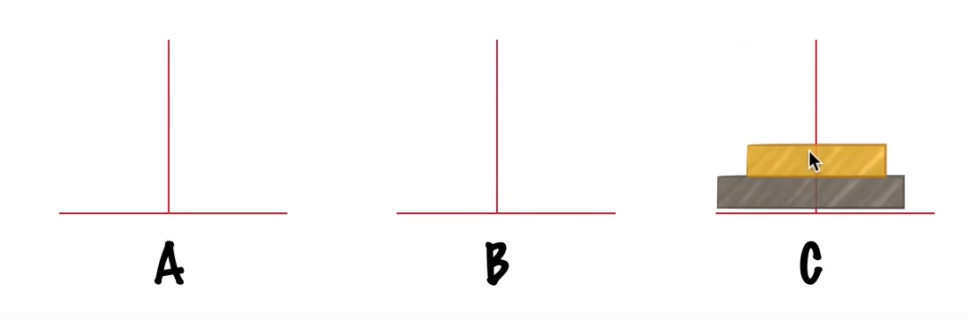
  

• 当n个盘时，思路是将A上的n-1个盘看做是一个小盘，将A最下面的大盘看做是一个大盘，此时即和n=2时的思路一致了
  
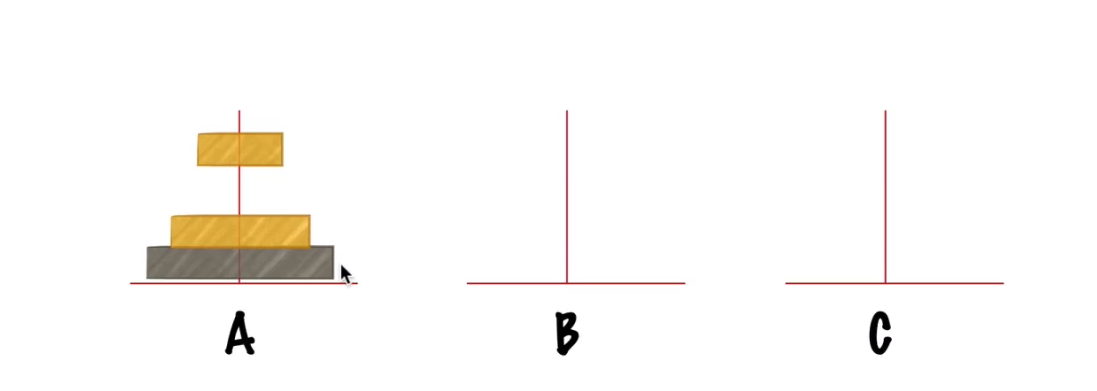
  步骤一：将A上n-1个盘移动到B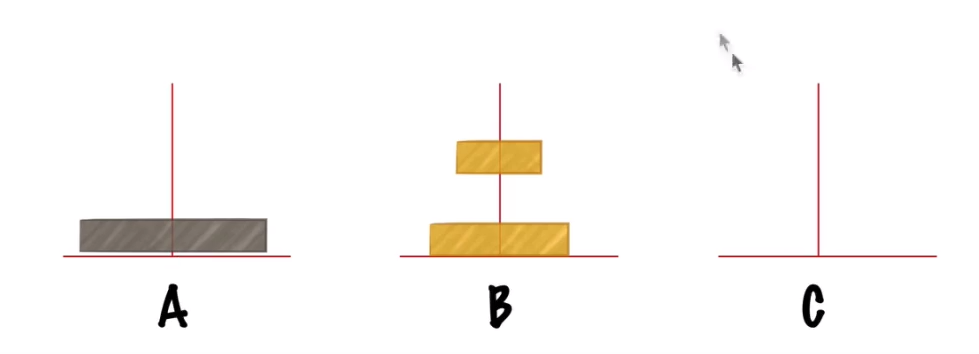
  
  步骤二：将A上最下面的大盘移动到C盘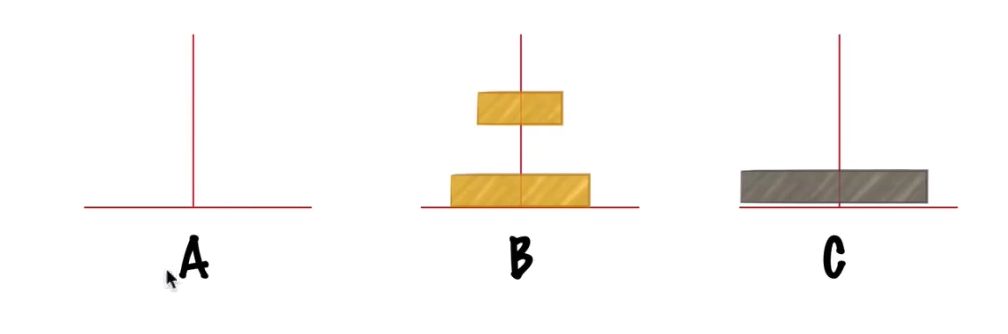
  
  步骤三：将B上的n-1个盘移动到C盘上

• 算法实现如下：

def hanoi(n,a,b,c):
    """
    将n个盘从a经过b移动到c
    :param n:
    :param a:
    :param b:
    :param c:
    :return:
    """
    if n>0:
        hanoi(n-1,a,c,b)
        print(f"moving {n} from {a} to {c}")
        hanoi(n-1,b,a,c)

if __name__=="__main__":
    print("---------------- n=2 -----------------------------")
    hanoi(2,"A","B","C")
    print("---------------- n=3 -----------------------------")
    hanoi(3, "A", "B", "C")
    print("---------------- n=4 -----------------------------")
    hanoi(4, "A", "B", "C")

执行结果如下：

---------------- n=2 -----------------------------
moving 1 from A to B
moving 2 from A to C
moving 1 from B to C
---------------- n=3 -----------------------------
moving 1 from A to C
moving 2 from A to B
moving 1 from C to B
moving 3 from A to C
moving 1 from B to A
moving 2 from B to C
moving 1 from A to C
---------------- n=4 -----------------------------
moving 1 from A to B
moving 2 from A to C
moving 1 from B to C
moving 3 from A to B
moving 1 from C to A
moving 2 from C to B
moving 1 from A to B
moving 4 from A to C
moving 1 from B to C
moving 2 from B to A
moving 1 from C to A
moving 3 from B to C
moving 1 from A to B
moving 2 from A to C
moving 1 from B to C