前言

以下笔记是天勤版本的考研数据结构数据书籍
通过参考其书籍做下的笔记

图是一种比线性表和树更为复杂的数据结构。在线性表中，数据元素之间仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继；在 树形结构中，数据元素之间有着明显的层次关系，并且每一层中的数据元素可能和下一层中的多个元素（即其孩子结点）相关，但只能和上一层中一个元素（即其双亲结点）相关； 而在图结构中，结点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。

1. 定义

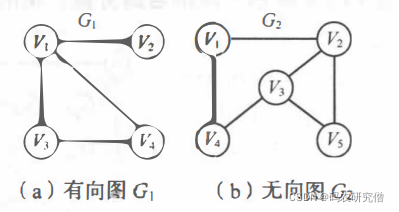
图(Graph) G由两个集合V和E组成，记为G=(V,E) , 其中V是顶点的有穷非空集合，E是V中顶点偶对的有穷集合，这些顶点偶对称为边。V(G)和E(G)通常分别表示图G的顶点集合和边集合，E(G)可以为空集。若E(G)为空，则图G只有顶点而没有边。

分有向图和无向图
有向图：顶点对<x, y>是有序的，它称为从顶点 x到顶点 y的一条有向边。 因此’<x,y>与<y, x>是不同的两条边
在无向图：，顶点对 ( x, y)是无序的，它称为顶点 x到顶点 y关联的一条边

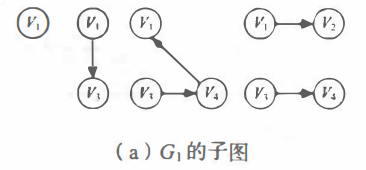
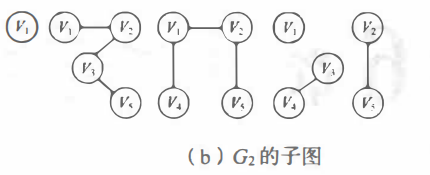
• 子图：类似集合的包含关系
• 无向完全图和有向完全图：无向图，若具有 n(n- 1)/2 条边，则称为无向完全图。对于有向图，若具有n(n- 1)条弧，则称为有向完全图
• 权和网：每条边可以标上具有某种含义的数值，该数值称为该边上的权。
  这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网
• 度、入度和出度：
  顶点的度是指和其相关联的边的数目
  对于有向图，顶点v的度分为入度和出度。入度是以顶点v为头的弧的数目， 出度是以顶点 v 为尾的弧的数目
• 回路或环：第一个顶点和最后一个顶点相同的路径称为回路或环
• 简单路径、 简单回路或简单环：
  序列中顶点不重复出现的路径称为简单路径。
除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环
• 连通、连通图和连通分量：
  无向图种，顶点和顶点相通，称为之连通
  （连通图和连通分量具体如下）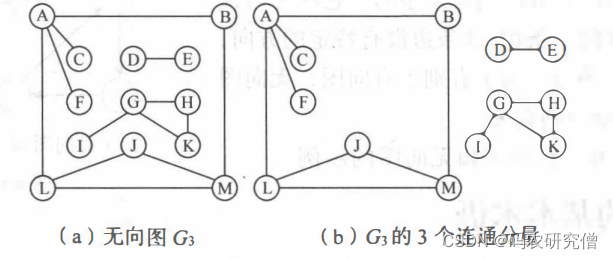
  
• 强连通图和强连通分量：
  在有向图 G 中，顶点到顶点的路径都存在路径，则称是强连通图。
  有向图中的极大强连通子图称作有向图的强连通分量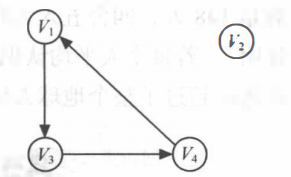
  

2. 存储结构

图没有顺序存储结构，但可以借助二维数组来表示元素之间的关系，即邻接矩阵表示法。另一方面，图的任意两个顶点间都可能存在关系，因此，用链式存储表示图是很自然的事，图的链式存储有多种，有邻接表、十字链表和邻接多重表，应根据实际需要的不同选择不同的存储结构

2.1 邻接矩阵

邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵

无向图的表示：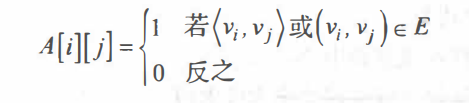

有向图的表示：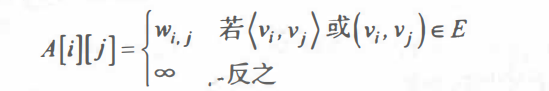

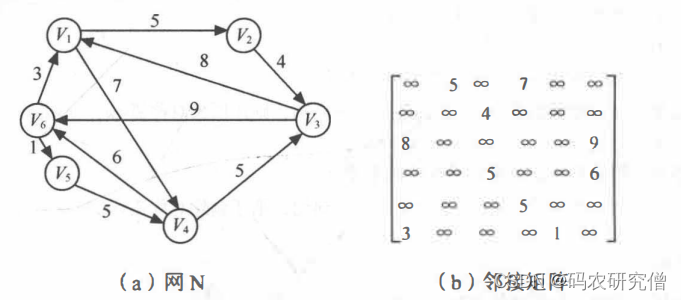
其结构表示如下所示

//-----图的邻接矩阵存储表示－－－－－
#define Maxint 32767 //表示极大值， 即 ∞
#define MVNum 100 //最大顶点数
typedef char VerTexType;//假设顶点的数据类型为字符型
typedef int ArcType;//假设边的权值类型为整型
typedef struct
{
	VerTexType vexs [MVNum] ; //顶点表
	ArcType arcs[MVNum) [MVNum); //邻接矩阵
	int vexnum,arcnum; //图的当前点数和边数
} AMGraph; 

采用邻接矩阵表示法创建无向网
已知一个图的点和边， 使用邻接矩阵表示法来创建此图的方法比较简单， 下面以一个无向网为例来说明创建图的算法

算法步骤:

• 输入总顶点数和总边数。
• 依次输入点的信息存入顶点表中。
• 初始化邻接矩阵， 使每个权值初始化为极大值
• 构造邻接矩阵。依次输入每条边依附的顶点和其权值，确定两个顶点在图中的位置之后，使相应边赋予相应的权值，同时使其对称边赋予相同的权值。

Status CreateUDN(AMGraph &G) 
{//采用邻接矩阵表示法，创建无向网G
	cin>>G.vexnum>>G.arcnum; //输人总顶点数，总边数
	
	for(i=O;i<G.vexnum;++i) //／／依次输入点的信息
		cin>>G.vexs[i); 
		
	for(i=O;i<G.vexnum;++i) //初始化邻接矩阵，边的权值均置为极大值Maxint
		for (j =0; j <G. vexnum; ++j) 
			G.arcs[i) [j)=Maxint;
			
	for(k=O;k<G.arcnum;++k) //构造邻接矩阵
	{
		cin>>vl>>v2>>w; //输人一条边依附的顶点及权值
		i=LocateVex(G,v1);j=LocateVex(G,v2); //确定v1和v2在G中的位置，即顶点数组的下标
		G.arcs[i) [j)=w; //边<v1, v2>的权值置为w
		G.arcs[j] [i]=G.arcs[i] [j];//置<v1, v2>的对称边<v2, v1>的权值为w
	}
	return OK;
}

优缺点如下：

优点

• 便于判断两个顶点之间是否有边， 即根据A[i][j] = 0或1来判断。
• 便于计算各个顶点的度。对于无向图，邻接矩阵第i个元素之和就是顶点i的度；对于有向图，第i行元素之和就是顶点 i 的出度，第i 列元素之和就是顶点i的入度。

缺点

• 不便于增加和删除顶点
• 不便于统计边的数目，需要扫描邻接矩阵所有元素才能统计完毕，时间复杂度为O(n²)
• 空间复杂度高。如果是有向图，n个顶点需要n2个单元存储边。如果是无向图，因其邻接矩阵是对称的，所以对规模较大的邻接矩阵可以采用压缩存储的方法，仅存储下三角（或上三角）的元素，这样需要n(n-1)/2个单元即可。但无论以何种方式存储，邻接矩阵表示法的空间复杂度均为O(n²)，这对于稀疏图而言尤其浪费空间。

2.2 邻接表

邻接表(Adjacency List) 是图的一种链式存储结构。在邻接表中，对图中每个顶点Vi ; 建立一个单链表，把与 Vi 相邻接的顶点放在这个链表中。邻接表中每个单链表的第一个结点存放有关顶点的信息， 把这一结点看成链表的表头， 其余结点存放有关边的信息， 这样邻接表便由两部分组成：表头结点表和边表

(1) 表头结点表：由所有表头结点以顺序结构的形式存储， 以便可以随机访问任一顶点的边链表。表头结点包括数据域 (data) 和链域 (firstarc) 两部分
(2)边表：由表示图中顶点间关系的 2n个边链表组成。 边链表中边结点包括邻接点域(adjvex)、数据域 (info) 和链域 (nextarc) 三部分

在无向图的邻接表中， 顶点 Vi 的度恰为第i个链表中的结点数；而在有向图中， 第i 个链表中的结点个数只是顶点 Vi 的出度， 为求入度，必须遍历整个邻接表。

//- - - - -图的邻接表存储表示－ －－－－
#define MVNum 100 //最大顶点数
typedef struct ArcNode //边结点
{ 
	int adjvex; //该边所指向的顶点的位置
	struct ArcNode * nextarc; //指向下一条边的指针
	Otherinfo info; //和边相关的信息
}ArcNode; 

typedef struct VNode //顶点信息
{
VerTexType data; 
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
) VNode,AdjList[MVNum]; //AdjLst表示邻接表类型

typedef struct //邻接表
AdjList vertices; 
int vexnum,arcnum; //图的当前顶点数和边数
}ALGraph;

创建无向图
算法步骤：

• 输入总顶点数和总边数。
• 依次输入点的信息存入顶点表中，使每个表头结点的指针域初始化为NULL。
• 创建邻接表。依次输入每条边依附的两个顶点， 确定这两个顶点的序号i 和 j 之后， 将此边结点分别插入 Vi 和vj 对应的两个边链表的头部。

Status CreateUDG(ALGraph &G) 
{//采用邻接表表示法， 创建无向图 G
	cin>>G.vexnum>>G.arcnum; //输入总顶点数， 总边数
	for(i=O;i<G.vexnum;++i) //输入各点，构造表头结点表
	{
		cin»G.vertices[i) .data; //输入顶点值
		G.vertices[i) .firstarc=NULL;//初始化表头结点的指针域为NULL
	}
	
	for(k=O;k<G.arcnum;++k) //输入各边， 构造邻接表
	{
		cin>>v1>>v2; //输入 一条边依附的两个顶点
		i=LocateVex(G,v1); j =LocateVex(G,v2); 
		//确定vl和 v2在G中位置， 即顶点在G.vertices中的序号
		p1=new ArcNode; //生成一个新的边结点*pl
		p1->adjvex=j; //邻接点序号为j
		p1->nextarc=G. vertices [i] . firstarc; G. vertices [i]. firstarc= p1; 
		//将新结点*pl插入顶点Vi的边表头部
		p2=new ArcNode; //生成另一个对称的新的边结点*p2
		p2->adjvex=i; //邻接点序号为i
		p2->nextarc=G.vertices[j] .firstarc; G.vertices[j] .firstarc=p2; 
		//将新结点*p2插入顶点Vj的边表头部
	}
	return ok;
}

值得注意的是，一个图的邻接矩阵表示是唯一的，但其邻接表表示不唯一，这是因为邻接表表示中，各边表结点的链接次序取决于建立邻接表的算法，以及边的轮入次序

其优点：

• 便于增加和删除顶点。
• 便于统计边的数目， 按顶点表顺序扫描所有边表可得到边的数目，时间复杂度为o（n+e）
• 空间效率高。对于一个具有n个顶点e条边的图 G, 若 G 是无向图，则在其邻接表表示中有 n 个顶点表结点和 2e 个边表结点；若 G 是有向图，则在它的邻接表表示或逆邻接表表示中均有 n 个顶点表结点和e个边表结点。因此，邻接表或逆邻接表表示的空间复杂度为 O(n + e), 适合表示稀疏图。对于稠密图，考虑到邻接表中要附加链域，因此常采取邻接矩阵表示法。

缺点：

• 不便于判断顶点之间是否有边，要判定 Vi 和vj 之间是否有边，就需扫描第i个边表，最坏情况下要耗费 O(n)时间。
• 不便于计算有向图各个顶点的度。对于无向图，在邻接表表示中顶点Vi 的度是第i个边表中的结点个数。 在有向图的邻接表中，第 i 个边表上的结点个数是顶点 Vi的出度，但求 Vi的入度较困难，需遍历各顶点的边表。若有向图采用逆邻接表表示，则与邻接表表示相反，求顶点的入度容易，而求顶点的出度较难。

3. 图的遍历

和树的遍历类似，图的遍历也是从图中某一顶点出发，按照某种方法对图中所有顶点访问且仅访问一次。 图的遍历算法是求解图的连通性问题、 拓扑排序和关键路径等算法的基础

通常有两条遍历图的路径：深度优先搜索和广度优先搜索。 它们对无向图和有向图都适用

3.1 深度优先搜索

深度优先搜索(DepthFirst Search, DFS)遍历类似于树的先序遍历，是树的先序遍历的推广

步骤如下：

1. 从图中某个顶点v出发， 访问v。
2. 找出刚访问过的顶点的第一个未被访问的邻接点， 访问该顶点。 以该顶点为新顶点，重复此步骤， 直至刚访问过的顶点没有未被访问的邻接点为止。
3. 返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点， 访问该顶点。
4. 重复步骤 (2) 和(3), 直至图中所有顶点都被访问过，搜索结束

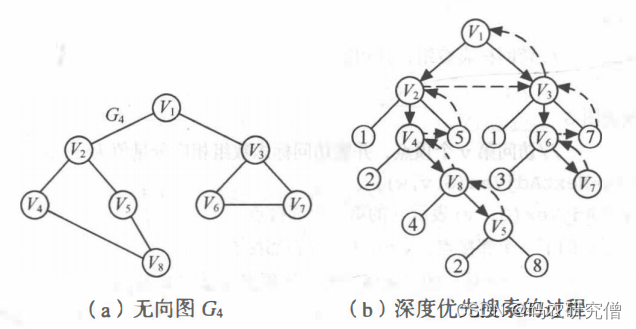
以上面这个实图为例：

1. 从顶点 V1出发， 访问 V1
2. 在访问了顶点 V1 之后，选择第一个未被访问的邻接点 V2, 访问 V2。 以 V2为新顶点，重复此步， 访问 V4, V8 、 V5。 在访问了 V5 之后， 由于 V5 的邻接点都已被访问， 此步结束。
3. 搜索从 V5 回到 V8, 由于同样的理由，搜索继续回到 V4, V2直至 V1, 此时由于 V1 的另一个邻接点未被访问， 则搜索又从 V1 到 V3, 再继续进行下去。 由此， 得到的顶点访间序列为：V1-V2-V4-V8-V5-V3-V6-V7

显然， 深度优先搜索遍历连通图是一个递归的过程。 为了在遍历过程中便于区分顶点是否已被访问，需附设访问标志数组 visited[n] , 其初值为 “false”, 一旦某个顶点被访问，则其相应的分量置为 “true”

深度优先搜索遍历连通图
算法步骤：

• 从图中某个顶点 v 出发， 访问 v, 并置 visited[v]的值为 true。
• 依次检查 v 的所有邻接点 w, 如果 visited[w]的值为 false, 再从 w 出发进行递归遍历，直到图中所有顶点都被访问过

bool visited [MVNum) ; 
void DFS(Graph G,int v) 
{//从第 v 个顶点出发递归地深度优先遍历图G
	cout<<v;visited[v)=true; 
	//访问标志数组， 其初值为 "false"
	//访问第 v 个顶点， 并置访问标志数组相应分扯值为 true
	for(w=FirstAdjVex(G,v);w>=O;w=NextAdjVex(G,v,w)) 
	//依次检查 v 的所有邻接点 w , FirstAdjVex (G, v)表示 v 的第一个邻接点
	//NextAdjVex(G,v,w)表示 v 相对于 w 的下一个邻接点， w>=0表示存在邻接点
		if(!visited[w]) DFS(G,w); //对 v 的尚未访问的邻接顶点 w 递归调用 DFS
}

深度优先搜索遍历非连通图

void DFSTraverse(Graph G) 
{//对非连通图G做深度优先遍历
	for(v=O;v<G.vexnum;++v) visited[v]=false; //访问标志数组初始化
	for(v=O;v<G.vexnum;++v)
		if(!visited[v]) DFS(G,v);
}

采用邻接矩阵表示图的深度优先搜索遍历

void DFS_AM(AMGraph G,int v) 
{//图G为邻接矩阵类型，从第v个顶点出发深度优先搜索遍历图G
	cout<<v;visited[v]=true; //访问第v个顶点，并置访问标志数组相应分址值为true
	for(w=O;w<G.vexnum;w++) //依次检查邻接矩阵 v所在的行		
		if((G.arcs[v] [w] !=O}&&(!visited[w]}} DFS(G,w}; 
		//G.arcs[v] [w] ! =0表示w是v的邻接点， 如果w未访问， 则递归调用DFS
}

采用邻接表表示图的深度优先搜索遍历

void DFS_AL (ALGraph G,int v) 
{//图G为邻接表类型， 从第v个顶点出发深度优先搜索遍历图G
	cout<<v;visited[v]=true; //访问第v个顶点，并置访问标志数组相应分量值为true
	p=G.vertices[v] .firstarc; //p指向v的边链表的第一个边结点
	while(p!=NULL) //边结点非空
	{
		w=p->adjvex;//表示w是v的邻接点
		if(!visited[w]) DFS(G,w); //如果口未访问， 则递归调用DFS
		p=p->nextarc;//p指向下一个边结点
	}
}

算法复杂度分析：
分析上述算法，在遍历图时，对图中每个顶点至多调用一次 DFS 函数，因为一旦某个顶点被标志成巳被访问，就不再从它出发进行搜索。 因此，遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间则取决于所采用的存储结构。 当用邻接矩阵表示图时，查找每个顶点的邻接点的时间复杂度为 O(n²), 其中 n为图中顶点数。而当以邻接表做图的存储结构时，查找邻接点的时间复杂度为O(e), 其中e为图中边数。由此， 当以邻接表做存储结构时，深度优先搜索遍历图的时间复杂度为 O(n + e)。

3.2 广度优先搜索

广度优先搜索(Breadth First Search, BFS)遍历类似于树的按层次遍历的过程

算法步骤:

• 从图中某个顶点v出发，访问v
• 依次访问v的各个未曾访问过的邻接点
• 分别从这些邻接点出发依次访问它们的邻接点， 并使 “先被访问的顶点的邻接点“ 先于”后被访问的顶点的邻接点” 被访问。重复步骤(3), 直至图中所有已被访问的顶点的邻接点都被访问到

和深度优先搜索类似，广度优先搜索在遍历的过程中也需要一个访问标志数组

广度优先搜索遍历连通图
算法步骤：

1. 从图中某个顶点 v 出发， 访问 v, 并置 visited[v]的值为 true, 然后将 v 进队。
2. 只要队列不空， 则重复下述操作：
   队头顶点 u 出队；
   依次检查 u 的所有邻接点 w, 如果 visited[w]的值为 false, 则访问 w, 并置 visited[w]的值为 true, 然后将 w 进队。

void BFS{Graph G,int v) 
{ //按广度优先非递归遍历连通图G
	cout<<v;visited[v]=true; //访问第v个顶点，并置访问标志数组相应分址值为true
	InitQueue{Q); //辅助队列Q初始化， 置空
	EnQueue{Q,v);//v进队
	while ( ! QueueEmpty {Q)) // 队列非空
	for(w=FirstAdjVex(G,u);w>=O;w=NextAdjVex(G,u,w))
	//依次检查u的所有邻接点w, FirstAdjVex(G,u)表示u的第一个邻接点
	//NextAdjVex(G,u,w)表示u相对于w的下一个邻接点，w>=0表示存在邻接点
		if (!visited [w]) //w为u的尚未访问的邻接顶点
		{
			cout<<w; visited[w]=true; //访问 w, 并置访问标志数组相应分扯值为true
			EnQueue (Q, w) ; //w进队
		}
	}
}

若是非连通图，上述遍历过程执行之后，图中一定还有顶点未被访问，需要从图中另选一个未被访问的顶点作为起始点，重复上述广度优先搜索过程，直到图中所有顶点均被访问过为止

分析上述算法，每个顶点至多进一次队列。
遍历图的过程实质上是通过边找邻接点的过程，因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同，即当用邻接矩阵存储时，时间复杂度为O(n²). 用邻接表存储时，时间复杂度为O(n+ e)。两种遍历方法的不同之处仅仅在于对顶点访问的顺序不同

4. 图的应用

介绍图的几个常用算法，包括最小生成树，最短路径、拓扑排序和关键路径算法。

4.1 最小生成树

普里姆 (Prim) 算法和克鲁斯卡尔 (Kruskal) 算法是两个利用 MST 性质构造最小生成树的算法。

4.1.1 普里姆算法

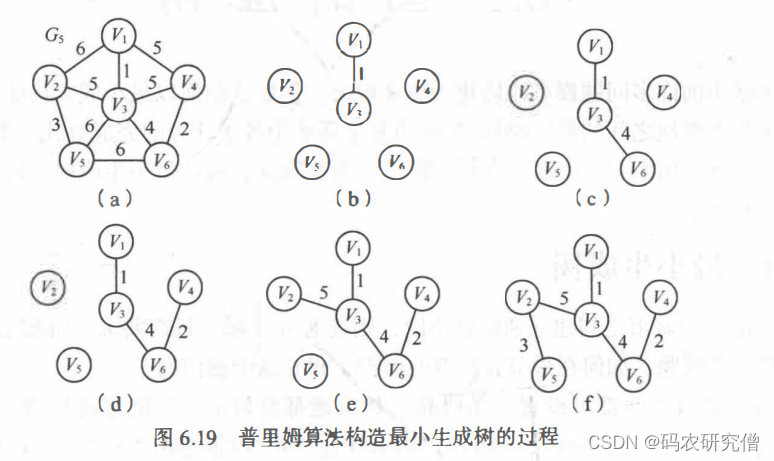
每次选择最小边时， 可能存在多条同样权值的边可选， 此时任选其一即可

其数据结构的构造如下

struct
{ 
VerTexType adjvex; //最小边在U中的那个顶点
ArcType lowcost; //最小边上的权值
} closedge [MVNum) ;

其算法步骤：

1. 首先将初始顶点 u加入U中，对其余的每一个顶点 Vj, 将closedge[j]均初始化为到 u 的边信息。
2. 循环 n -1 次， 做如下处理：
   • 从各组边 closedge 中选出最小边 closedge[k], 输出此边；
   • 将K加入U中；
   • 更新剩余的每组最小边信息 closedge[j], 对于 v-u中的边， 新增加了一条从 K 到j 的边， 如果新边的权值比 closed ge[i].lowcost 小，则将 closedge切.lowcost 更新为新边的权值。

void MiniSpanTree_Prim(AMGraph G,VerTexType u) 
{//无向网G以邻接矩阵形式存储， 从顶点u出发构造G的最小生成树T, 输出T的各条边
	k=LocateVex(G,u); //k 为顶点 u 的下标
	
	for(j=O;j<G.vexnum;++j) //对v-u 的每一个顶点 Vj, 初始化 closedge[j]
		if(j!=k) closedge[j]={u,G.arcs[k][j]}; //{adjvex, lowcost} 
		
	closedge[k].lowcost=O; //初始， U={u}
	for(i=1;i<G.vexnum;++i) 
	{//选择其余 n-1 个顶点，生成 n-1 条边(n=G.vexnum)
		k=Min(closedge); 
		//求出 T 的下一个结点：第 K 个顶点， closedge[k]中存有当前最小边
		uO=closedge[k] .adjvex; //	//uO 为最小边的一个顶点，uO属于U
		vO=G.vexs[k]; //vO 为最小边的另一个顶点
		cout<<uO<<vO; //输出当前的最小边(uO, vO) 
		closedge[k] .lowcost=O; //第k个顶点并入u集
		for(j=O;j<G.vexnum;++j) 
			if(G.arcs[k] [j]<closedge[j] .lowcost) //新顶点并入u 后重新选择最小边
				closedge [j]={G.vexs [k] ,G.arcs [k] [j]};
	}
}

4.1.2 克鲁斯卡尔算法

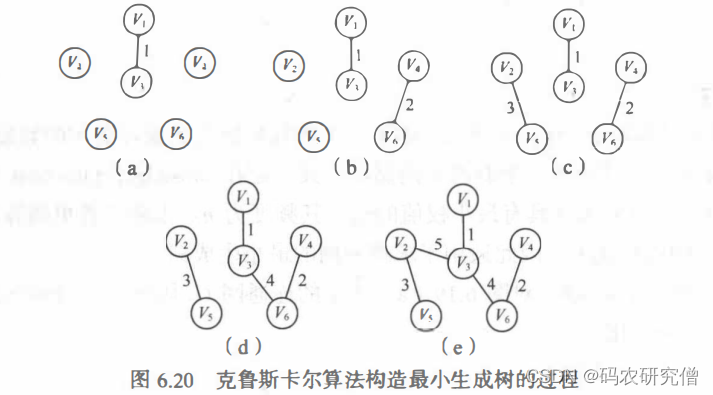
可以看出，克鲁斯卡尔算法逐步增加生成树的边，与普里姆算法相比，可称为“加边法”。与普里姆算法一样， 每次选择最小边时， 可能有多条同样权值的边可选， 可以任选其一

算法步骤：

1. 少将数组Edge中的元素按权值从小到大排序。
2. 依次查看数组Edge中的边，循环执行以下操作：
   • 依次从排好序的数组Edge中选出一条边(U1,U2）
   • 在Vexset中分别查找V1和V2所在的连通分量VS1和VS2, 进行判断：
   ► 如果VS1和VS2不等，表明所选的两个顶点分属不同的连通分量，输出此边，并合并VS1和VS2两个连通分量
   ► 如果VS1和VS2相等，表明所选的两个顶点属于同一个连通分量，舍去此边而选择下一条权值最小的边

void MiniSpanTree_ Kruskal(AMGraph G) 
{//无向网G以邻接矩阵形式存储，构造G的最小生成树T, 输出T的各条边
	Sort (Edge); //将数组 Edge 中的元素按权值从小到大排序
	for(i=O;i<G.vexnum;++i) //辅助数组，表示各顶点自成一个连通分址
		Vexset[i]=i; 
	for(i=O;i<G.arcnum;++i) //辅助数组，表示各顶点自成一个连通分址
	{
		v1=LocateVex(G,Edge[i] .Head); //v1 为边的始点 Head 的下标
		v2=LocateVex(G,Edge[i] .Tail); //v2 为边的终点 Ta过的下标
		vs1=Vexset[v1]; //获取边 Edge[i]的始点所在的连通分址 vs1
		vs2=Vexset[v2]; //获取边 Edge[i]的终点所在的连通分扯 vs2
		if(vs1!=vs2) //边的两个顶点分属不同的连通分扯
		{
			cout«Edge[i] .Head «Edge[i] .Tail;//输出此边
			for(j=O;j<G.vexnurn;++j) //合并 VS1 和 VS2 两个分量， 即两个集合统一编号
			if(Vexset[j] ==vs2) Vexset [j] =vs1; //集合编号为 vs2 的都改为 vs1
		}
	}
}

对于包含e条边的网，上述算法排序时间是 O(elog2e)。在 for 循环中最耗时的操作是合并两个不同的连通分量，只要采取合适的数据结构，可以证明其执行时间为 O(log2e), 因此整个 for 循环的执行时间是 O(elog2e), 由此，
克鲁斯卡尔算法的时间复杂度为 O(elog2e），与网中的边数有关，与普里姆算法相比，克鲁斯卡尔算法更适合千求稀疏网的最小生成树

4.2 最短路径

最常见的最短路径问题： 一 种是求从某个源点到其余各顶点的最短路径，另一种是求每一对顶点之间的最短路径

4.2.1 迪杰斯特拉算法

从某个源点到其余各顶点的最短路径

算法的实现要引入以下辅助的数据结构。

• 一维数组S[i]: 记录从源点Vo到终点Vi ;是否已被确定最短路径长度， true表示确定，false表示尚未确定。
• 一维数组 Path[i]: 记录从源点 Vo到终点 Vi 的当前最短路径上 Vi的直接前驱顶点序号。其初值为：如果从 Vo到 Vi 有弧，则 Path [i]为 v。；否则为-1。
• 一维数组 D[i]: 记录从源点 Vo到终点 Vi 的当前最短路径长度。其初值为：如果从 v。到 Vi 有弧，则 D[i)为弧上的权值；否则为 ∞

其算法步骤如下：

void ShortestPath_DIJ(AMGraph G, int vO)
{ //用Dijkstra算法求有向网G的vO顶点到其余顶点的最短路径
	n=G. vexnum; //n为G 中顶点的个数
	for (v= O;v<n; ++v) //n个顶点依次初始化
	{
		S[v]=false; //S初始为空集
		D[v]=G.arcs[vO][v];//将vO到各个终点的最短路径长度初始化为弧上的权值
		if(D[v]<Maxlnt) Path[v]=vO; //如果vO和v之间有弧， 则将v的前驱置为vO
		else Path[v]=-1; //如果vO 和v之间无弧， 则将v的前驱置为一1
	}
	S [vO] = true; //将vO加人 S
	D[vO]=O;//源点到源点的距离为 0

	for( i=1; i<n;++i) //对其余 n-1个顶点，依次进行计算
	{
		min= Maxlnt; 
		for(w= O;w<n;++w)
		if (! S [w] &&D [w] <min) 
		{
			v=w;min=D[w]; //选择一条当前的最短路径，终点为v
		} 
		S[v]=true; //将v加入S
		for(w=O;w<n;++w) //更新从v。出发到集合v-s上所有顶点的最短路径长度
		if (! S [w) && (D [v) +G. arcs [v) [w) <D [w])) 
		{ 
			D [w] =D [v] +G. arcs [v] [w]; 
			Path[w]=v; 
		}
	}
}

4.2.2 弗洛伊德算法

每一对顶点之间的最短路径

算法的实现要引入以 下辅助的数据结构。
(1) 二维数组 Path[i][j]：最短路径上顶点 Vj 的前一顶点的序号。
(2)二维数组D[i][j]：记录顶点 Vi和vj之间的最短路径长度。

算法步骤：

void ShortestPath_Floyd(AMGraph G)
{//用Floyd算法求有向网G中各对顶点1和）之间的最短路径
	for (i=O; i < G. vexnum; ++i) //对结点之间初始已知路径及距离
		for(j=O;j <G.vexnum;++j) 
		{
			D [ i ] [ j ] =G. arcs [ i ] [ j ] ;
			if(D[i] [j]<Maxint) Path[i] [j]=i; //如果 i和j之间有弧，则将j的前驱置为i.
			else Path[i] [j]=-1;				//如果 i和j之间无弧，则将j的前驱置为-1
		}
	for (k=O; k < G. vexnum; ++k) 
		for (i=O; i <G.vexnum;++i) 
			for(j=O;j <G.vexnum;++j) 
				if(D[i] [k]+D[k] [j] <D[i] [j])
				{
				D[i] [j]=D[i] [k]+D[k] [j]; 
				Path[i] [j]=Path[k] [j];
				}
}