一、算法介绍
1. 核心思想
《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding》
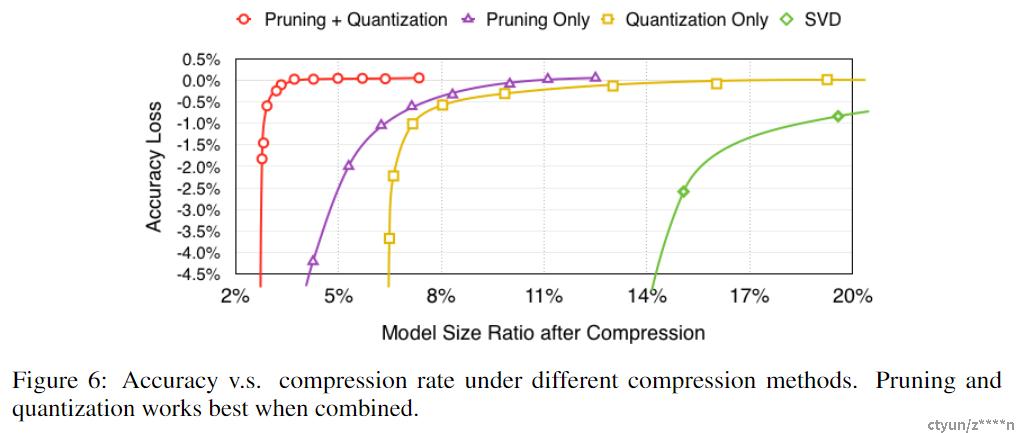
- 目标:降低大型神经网络的存储和计算消耗,使得深度学习框架可以在移动设备上运行。
- 1. 通过移除不重要的连接对网络进行剪枝;
- 2. 对权重进行量化,并使许多连接共享同一权重,并且只需要存储码本和索引;
- 3. 进行霍夫曼编码来利用有效权重的有偏分布。
- 流程图:
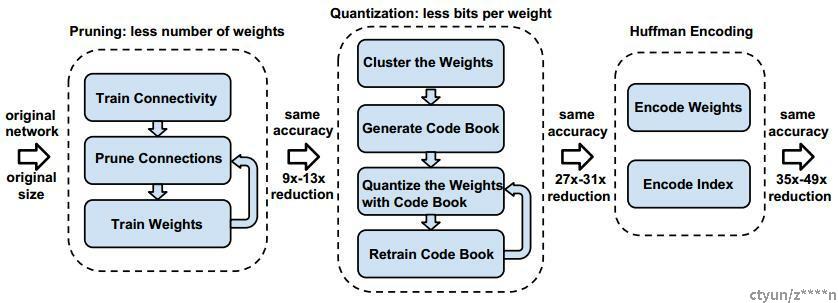
-
2. 详细过程
1)剪枝
在训练的过程中,会学到连接的参数。剪枝就是移除小于一定阈值的连接的权值,这样就会得到稀疏的网络连接。剪枝这一步能够将VGG-16(AlexNet)的参数降低到原来的1/13(1/9)。
由于网络中的冗余参数被移除,所以权重矩阵是稀疏化的,论文将稀疏矩阵用CSR和CSC的格式进行压缩,总共需要2a+n+1个存储单元,a是非零元素个数,n是行数或者列数。
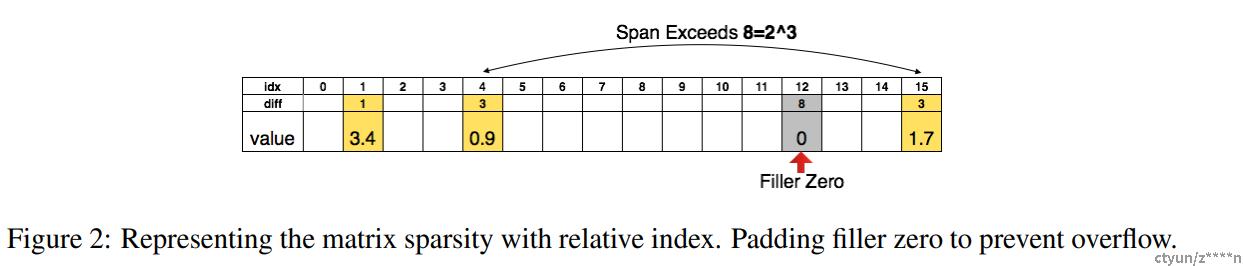
一个4*4的矩阵可以用一维16数组表示,剪枝时候,只保留 权值大于指定阈值的数,用相对距离来表示,例如idx=4和idx=1之间的位置差为3,如果位置差大于设定的span,那么就在span位置插入0。例如15和4之间距离为11大于span(8),所以在4+8的位置插入0,idx=15相对idx=12为3。这里span阈值在卷积层设置为8,全连接层为5。
2)权值量化和权值共享
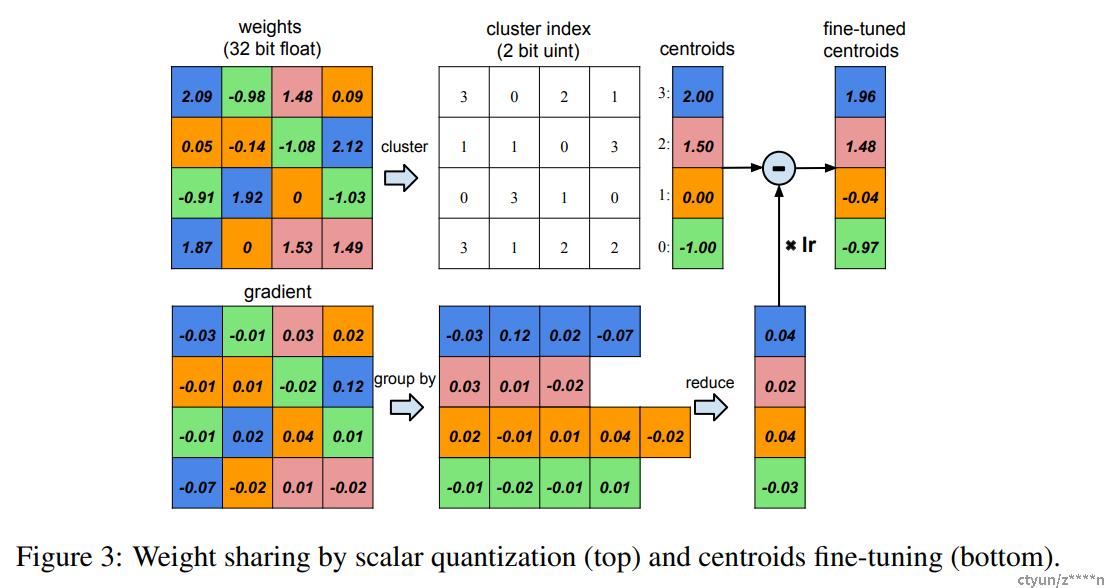
图3假定某层有4个输入单元4个输出单元,权重矩阵为4*4,梯度同样为4*4。假设权重被量化为4类,用四种颜色标识。用每类量化的值代表每类的权值,得到量化后的权值矩阵。用4个权值和16个索引就可以计算得到4*4权重矩阵连接的权值。梯度矩阵同样量化为4类,对每类的梯度进行求和得到每类的偏置,和量化中心一起更新得到新的权值。
压缩率计算方法如下公式所示:
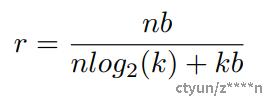
n代表连接数,b代表每一个连接需要b bits表示,k表示量化k个类,k类只需要用log2(k)个bit表示,n个连接需要 nlog2(k)索引,还需要用 kb表示量化中心的数值。
拿图3为例,有16个连接,每一个连接需要用32位的数值进行比较,量化为4类,每类只需要两个bit表示,每类的量化中心值32位。
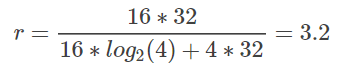
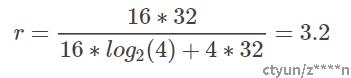
在量化为k个类时,作者采用了K-means聚类方法,把原始的n个权重 W={w1,w2,......,wn}使用聚类算法变为k个聚类中心 C={c1,c2,......,ck}。聚类算法最小化类内误差,目标函数如下所示:
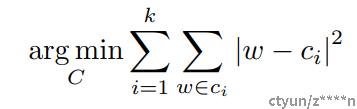
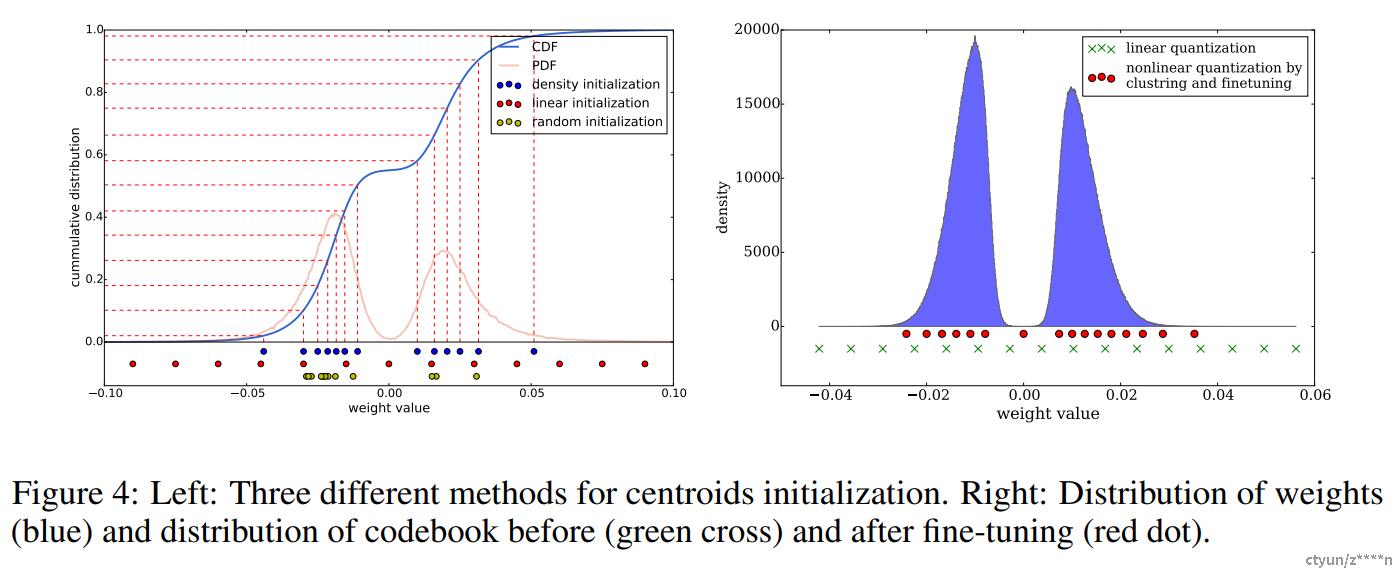
聚类中心的初始化也会影响网络的精度,作者提出了三种初始化方法,分别为:
- Forgy: 从原始的数据集中随机选取k个值作为聚类中心,从figure4可以看出,原始的数据符合双峰曲线,所以初始化的值集中在两个峰顶附近。
- Density-based:在Y轴平分CDF曲线,然后找到对应的X轴位置,作为初始化聚类中心。这种方法初始化距离中心也是在双峰附近,但是比Forgy相对稀疏。
- Linear:找到权值的最大值和最小值,在[min,max]区间内平均划分k份,作为原始的聚类中心。
但是在深度学习中,大的权值说明对该因素的影响大,但是实际上,大的权值在参数中很少,如果采用1,2方法进行初始化,可能会把大的权值量化为小的值,影响实际效果。所以线性的初始化效果最好。
量化之后,目标函数的求导就变为了量化后聚类中心的值的求导:
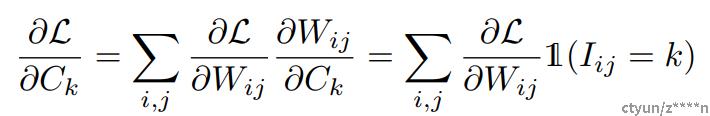
3)霍夫曼编码
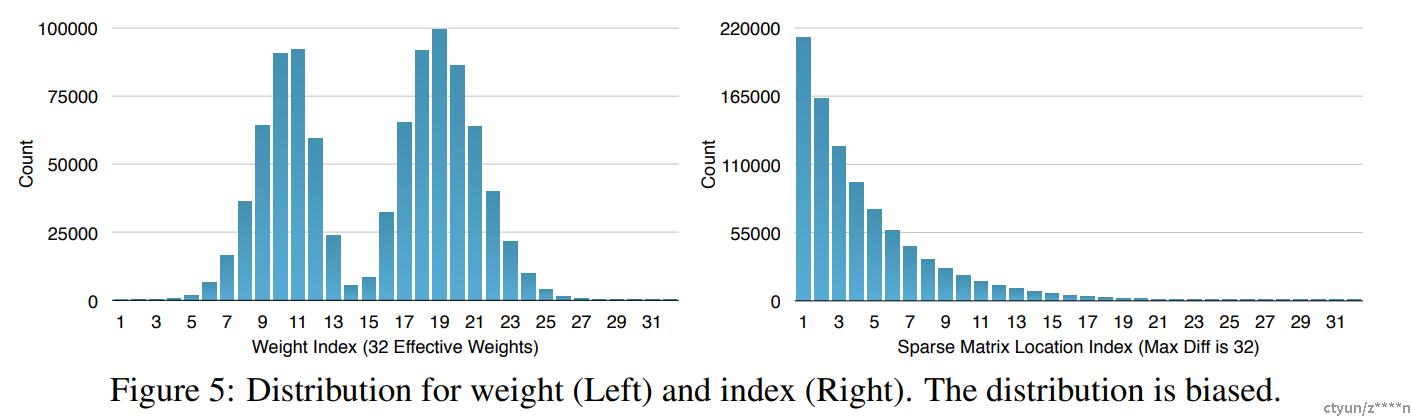
聚类中心,需要用log2(k)的bit作为索引,这里可以使用变长的霍夫曼编码进一步压缩。figure 5显示了压缩前和压缩后的长度分布。
 3. 实验
3. 实验
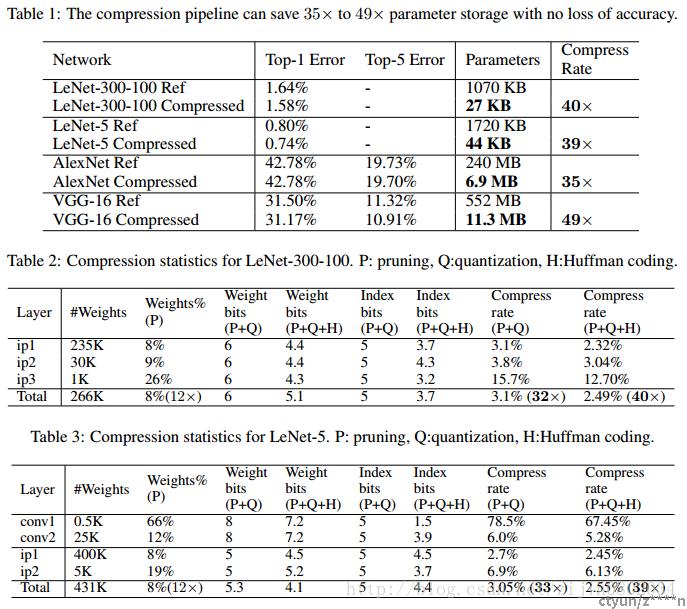
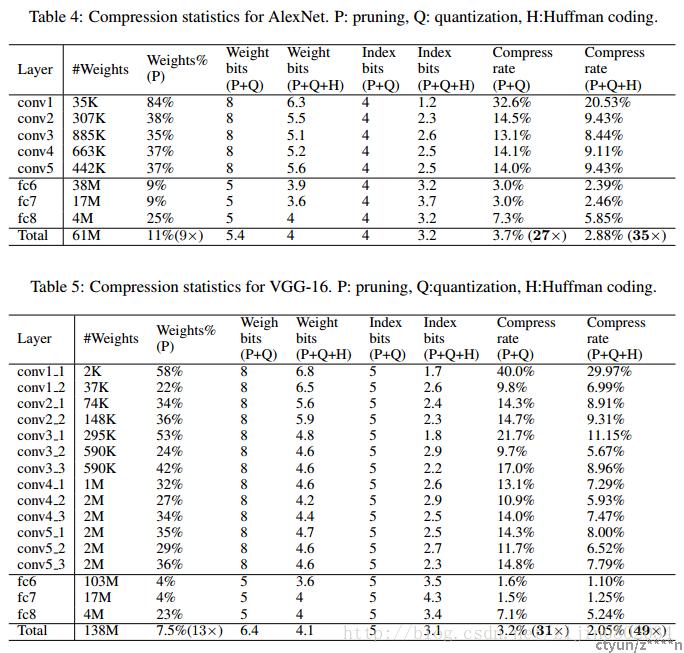
4. 结论
深度压缩可以在不影响准确率的情况下压缩神经网络。论文的方法通过修剪不重要的连接,使用权重共享量化网络,然后应用霍夫曼编码来操作。论文重点介绍了在 AlexNet 上的实验,该实验将权重存储减少了 35 倍而不会损失准确性。论文对 VGG-16 和 LeNet 网络显示了类似的结果,压缩了 49 倍和 39 倍,而不会损失准确性。这导致将卷积网络放入移动应用程序的存储需求更小。在深度压缩之后,这些网络的大小适合片上 SRAM 缓存,而不需要片外 DRAM 内存。这可能使深度神经网络在移动设备上运行时更加节能。论文的压缩方法还有助于在应用程序大小和下载带宽受到限制的移动应用程序中使用复杂的神经网络。
5. 讨论