昨天成功配置了环境，打印出来一张图，今天我们用线性方程来简单直白的理解

我有一组x和一组y，每一个x都对应到一个y上，我们让他再简单一点：

y = 2 * x + 5

他长这个样子：

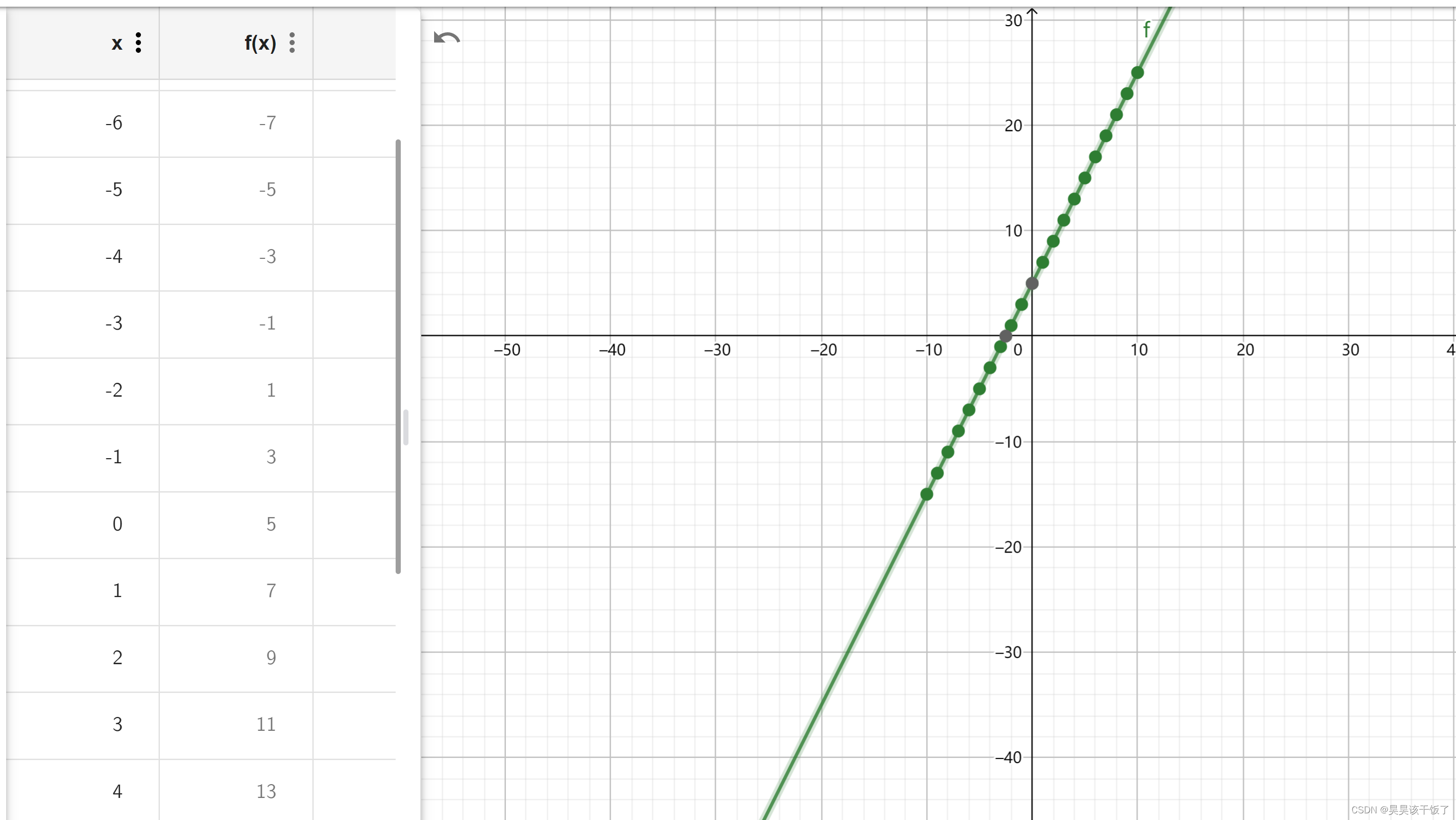
 现在我告诉计算机，y = a * x + b ，告诉你一些已知的点（训练），你生成一个a和b，这样我以后随意输入一个x，计算机都可以告诉我一个符合这个线性方程的y了。

我们假设给了计算机（1,7）（2,9）（3,11）。。。。。。200个点，下面的过程其实就是训练模型了：

1.初始值，假设这个时候计算机随机给了a=1,b=1，然后每次调整走 1（实际学习中通常0.0001）

那也就是

 y = 1 * x + 1

长这个样子，和我们目标差很多：

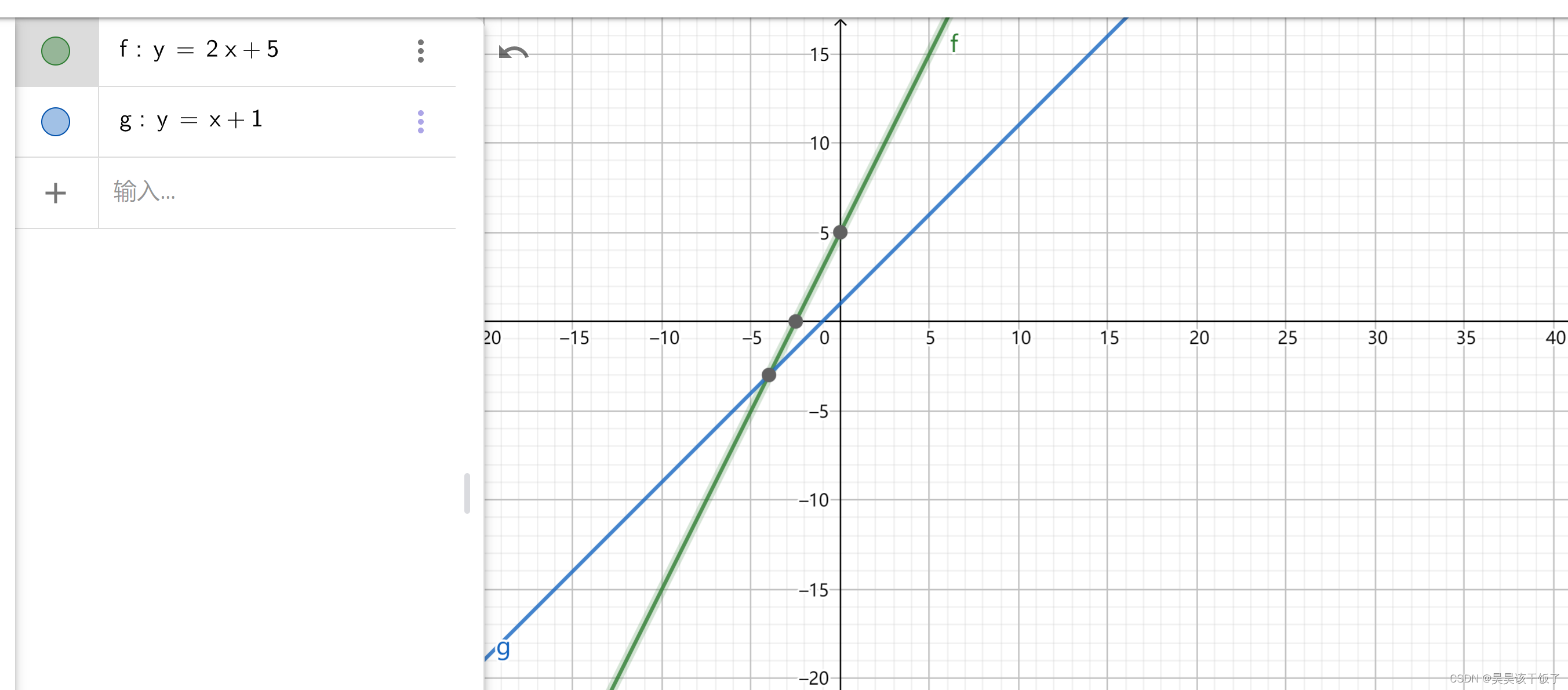
2.计算验证损失

得到了初始值，他用第一组（1,7）中的 x 来计算，得到了 2，这显然和 7 不太对呀，7 - 2 = 5这就是损失了的数值（损失详细原理会单开一页）

3.优化

（具体优化原理也分开了）经过一系列操作，计算机决定将a，b分别调整为 2，2，此时为

y = 2 * x + 2

重复2 3，直到，再次输入x，计算机计算的结果和给出的结果一致，我们得到了y = 2 * x + 5

当然，实际中可能计算机得出的数会无限接近正确答案，但只有在线性方程中，才有可能得到一个准确的值，训练了一千次，损失值已经到了-28次，很小很小，我的a = 2，b也无限接近于5了：

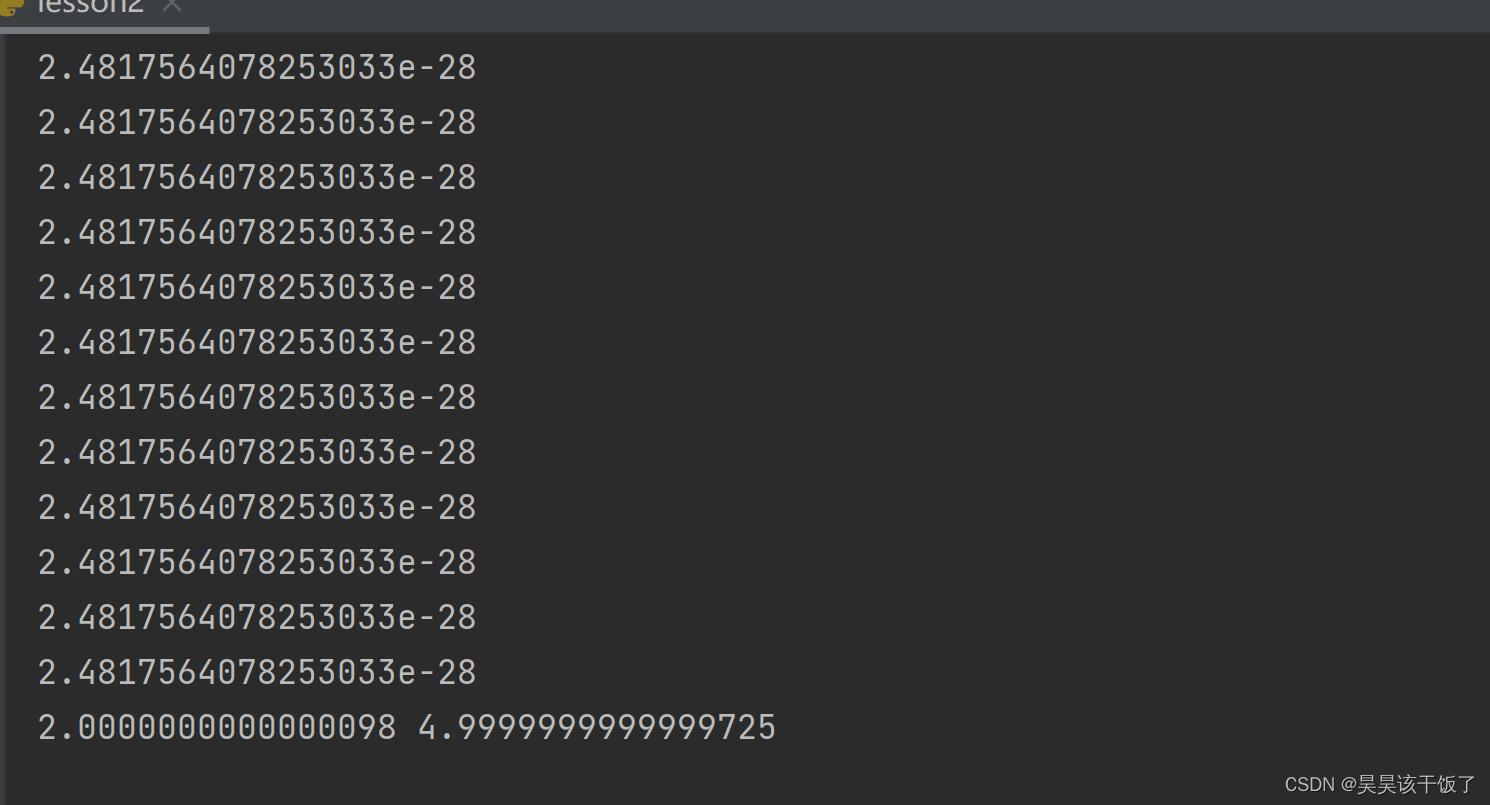
整个项目代码：

import numpy as np


X=list(range(5)) //定义x,y
Y=[]
for x in X:
   y = 2.0 * x + 5.0
   Y.append(y)

def loss(w, b, X,Y): //定义损失，计算差值取平均

    totalError = 0
    for i in range(len(X)):
        x = X[i]
        y = Y[i]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(X))


def update(w, b,  X,Y, learningRate): //定义优化,取导数
    b_gradient = 0
    w_gradient = 0
    N = float(len(X))
    for i in range(0, len(X)):
        x = X[i]
        y = Y[i]
        b_gradient += (2 / N) * ((w * x + b) - y)
        w_gradient += (2 / N) * x * ((w * x + b) - y)

    new_b = b - (learningRate * b_gradient)
    new_w = w - (learningRate * w_gradient)
    return new_w,new_b

learning_rate = 0.027 //学习率，就是上文中的 1，这里给了0.027
b = 0
w = 0
times = 10000 //重复10000次

for i in range(times):
    w,b = update(w, b,  X,Y, learning_rate)
    print(loss(w, b,X,Y))
print(w,b)

看一组实际应用于图像分类的损失和优化函数： 

opt = optimizers.SGD(learning_rate=0.0001)

loss = losses.CrossEntropyLoss()

        SGD对每一个样本进行梯度更新时，越是数量庞大的数据集，就越有可能会有相似的样本，所以SGD函数在一次更新时只执行一次，避免了数据的冗余，同时也降低了时间成本，并且可以根据结果新增样本。

        CrossEntropyLoss，使用交叉熵损失函数可以解决一些实例在刚开始训练时学习得非常慢的问题，其主要针对激活函数为Sigmod 函数，当输出的神经元是S型神经元时，更好的选择就是使用交叉熵损失函数，交叉熵无法改善隐藏层中神经元发生的学习缓慢，交叉熵损失函数只对网络输出明显背离预期时发生的学习缓慢有改善效果， 交叉熵损失函数并不能改善或避免神经元饱和，而是当输出层神经元发生饱和时，能够避免其学习缓慢的问题。