题目:计算并集分割成的子区间的样本密度平均值
有两组样本数据非均匀分布在区间[0,1] 内。区间存在两组分界点,![]() 和
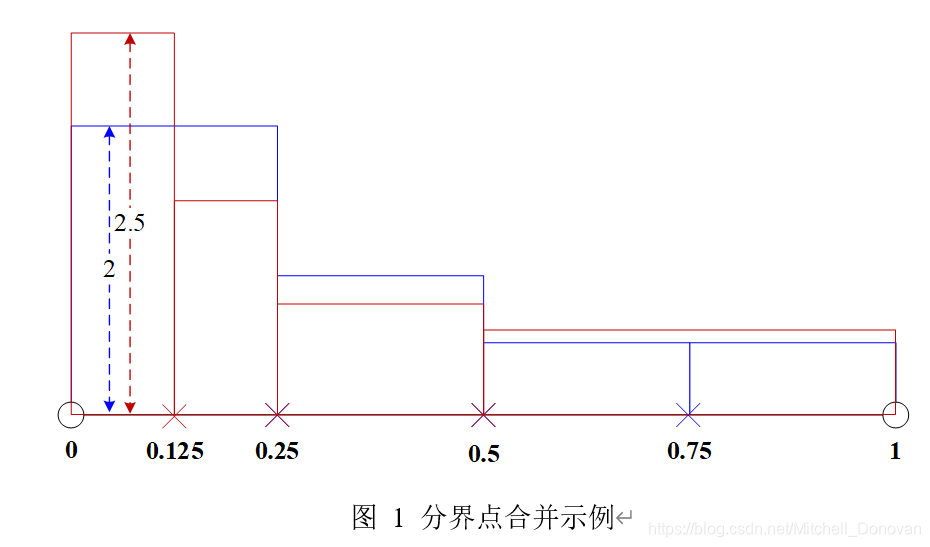
和![]() 。每组分界点个数为(K-1) ,这(K-1)个分界点将整个区间分割成K个子区间。已知每一组分界点的位置和由这组分界点分割成的K 个子区间的样本密度,请计算由这两组分界点的并集分割成的子区间的样本密度的平均值。如图1所示,区间[0,1]
。每组分界点个数为(K-1) ,这(K-1)个分界点将整个区间分割成K个子区间。已知每一组分界点的位置和由这组分界点分割成的K 个子区间的样本密度,请计算由这两组分界点的并集分割成的子区间的样本密度的平均值。如图1所示,区间[0,1]![]() 存在两组分界点{0.25,0.5,0.75} 和{0.125,0.25,0.5} 。由第一组样本点划分出的4个子区间样本密度分别为2、1、0.5、05,由第二组样本点划分出的4个子区间样本密度分别为2.5,1.5、0.8、0.6。以上两组分界点的并集为{0.125,0.25,0.5,0.75} ,包含4个分界点,这4个分界点将整个区间分割成5个子区间,可以计算每个区间样本密度的平均值。以第一个区间[0,0.125] 为例,其样本密度的平均值为
存在两组分界点{0.25,0.5,0.75} 和{0.125,0.25,0.5} 。由第一组样本点划分出的4个子区间样本密度分别为2、1、0.5、05,由第二组样本点划分出的4个子区间样本密度分别为2.5,1.5、0.8、0.6。以上两组分界点的并集为{0.125,0.25,0.5,0.75} ,包含4个分界点,这4个分界点将整个区间分割成5个子区间,可以计算每个区间样本密度的平均值。以第一个区间[0,0.125] 为例,其样本密度的平均值为![]() 。
。
输入样例:
3(每一组分界点的个数)
0.25 0.5 0.75(第一组分界点位置)
0.125 0.25 0.5 (第二组分界点位置)
2 1 0.5 0.5(由第一组分界点划分的区间样本密度)
2.5 1.5 0.8 0.6(由第二组分界点划分的区间样本密度)
输出样例:
2.25 1.75 0.9 0.55 0.55(由合并后的分界点划分的区间样本密度)
代码示例👇
//author:Mitchell_Donovan
//date:4.27
#include<iostream>
using namespace std;
int main() {
int size;
cout << "请输入节点个数:";
cin >> size;
double* Va = new double[size + 1];
double* Vb = new double[size + 1];
cout << "请输入第一组分界点值:";
for (int i = 0; i < size; i++) {
cin >> Va[i];
}
Va[size] = 1;
cout << "请输入第二组分界点值:";
for (int i = 0; i < size; i++) {
cin >> Vb[i];
}
Vb[size] = 1;
double* Pa = new double[size + 1];
double* Pb = new double[size + 1];
cout << "请输入第一组区间样本密度:";
for (int i = 0; i < size + 1; i++) {
cin >> Pa[i];
}
cout << "请输入第二组区间样本密度:";
for (int i = 0; i < size + 1; i++) {
cin >> Pb[i];
}
double a = Va[0], b = Vb[0];
int i = 0, j = 0;
while (a != 1 || b != 1) {
cout << (Pa[i] + Pb[j]) / 2 << " ";
if (a < b) {
a = Va[++i];
}
else if (a > b) {
b = Vb[++j];
}
else {
a = Va[++i];
b = Vb[++j];
}
}
cout << (Pa[i] + Pb[j]) / 2 << " ";
}输出示例👇


