前言

提示：这里可以添加本文要记录的大概内容：

递归是一种解决问题的奇妙方法，可以让计算机以很少的代码而完成大量的计算，下面来简单的看一下递归吧：

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、递归是什么？（函数自己调用自己）

递归：递指的是递推，归指的是回归，递推实际上是两个过程，一是先依次递归，然后依次回归，在C语言中，递推所呈现出来的是同一个函数的重复调用，且具有限制条件并逐步逼向限制条件的一种形式

递归的使用前提：

1.有限制条件，可以进行逐步分解
2.每次进行递归后都可以逼向这个限制条件
注意：不是所有的代码都能使用递归，递归是一种特殊方法，即使有一些代码满足限制条件，也会因为效率，代码读写的问题而不适用于递归的方法。

二、递归场景的导入：

比如，我们想要计算10^5
这个结果，我们可以将其拆分为10✖10^4
继续拆分为10✖10✖10^3
…
最终拆分为10✖10✖…✖10的这种形式
之后计算机为了求10^5
可以分解为10✖10^4,
那么计算机为了求10✖10^4,
必须先求10^4。。。
依次类推，
为了便于大家理解，我们直接上图来演示一波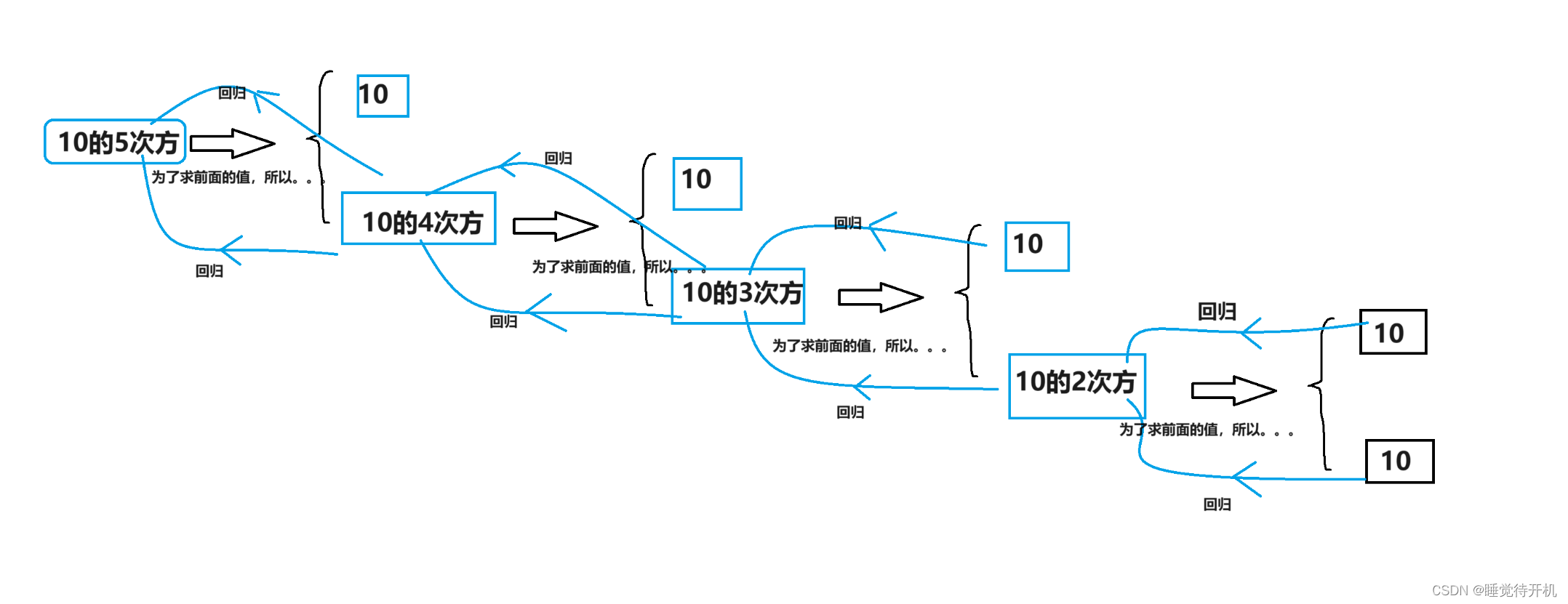

为了更深入的理解一下递归，我们不妨通过几个例子来探求：

三、递归的练习题：

eg1.计算n个斐波那契数字(递归)：

#define _CRT_SECURE_NO_WARNINGS 1
//计算n个斐波那契数字(递归)：

#include<stdio.h>
int Fib(int n)
{
	if (n == 1 || n == 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d ", ret);
	return 0;
}

eg2.使用递归实现某个数字的n次方

代码如下（示例）：

//使用递归实现某个数字的n次方
#include<stdio.h>
int power(int n, int k)
{
	if (k == 1)
		return n;
	else
		return (n * power(n,k-1));
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int k = 0;
	scanf("%d", &k);
	int ret = power(n,k);
	printf("%d的%d次方是%d ",n,k, ret);
	return 0;
}

eg3.计算一个数的每位之和（递归实现）

//计算一个数的每位之和（递归实现）
int c = 0;
sum(int num)
{
	c += num % 10;
	if (num < 10)
		return c;
	else
		return(sum(num / 10));
}
#include<stdio.h>
int main()
{
	int num = 0;
	scanf("%d", &num);
	int ret = sum(num);
	printf("%d ", ret);
	return 0;
}

---

eg4.递归的方法实现求阶乘

//方法一：递归的方法实现求阶乘
#include<stdio.h>
jp(int num)
{
	if (num == 1)
		return 1;
	else
		return num* jp(num - 1);
}
int main()
{
	int num = 0;
	scanf("%d", &num);
	printf("%d ",jp(num));
	return 0;
}

eg5:依次正打印某一个数字的每一位

#include<stdio.h>
int test(int num)
{
	if (num > 9)
	{
		test(num / 10);

	}
	printf("%d ", num % 10);
}

int main()
{
	int num = 0;
	scanf("%d", &num);
	test(num);
	return 0;
}

四、但是有些地方，也可以不用递归的方法实现：

比如：

eg1修改：计算n个斐波那契数字(非递归)：

//使用一般的逻辑方法来求第n个斐波那契数字：
#include<stdio.h>
int Fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 2;
	if (n == 1 || n == 2)
		return 1;
	else
	{
		if (n > 3)
		{
			while (n - 2)
			{
				c = a + b;
				a = b;
				b = c;
				n--;
			}
		}

		return c;
	}
}
int main()
{
	int n = 1;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);
	return 0;
}

eg2：使用非递归的方法实现阶乘：

//方法二：使用非递归的方法实现阶乘：
#include<stdio.h>
int main()
{
	int num = 0;
	scanf("%d", &num);
	int i = 0;
	int sum = 1;
	for (i = 1; i <= num; i++)
	{
		sum *= i;
	}
	printf("%d ", sum);
	return 0;
}

#include<stdio.h>
test(int num)
{
	if (num < 9)
		printf("%d ", num % 10);
	else
		while (num / 10)
		{
			num /= 10;
			test(num / 10);
		}
}

int main()
{
	int num = 0;
	scanf("%d", &num);
	test(num);
	return 0;
}

并且，我们需要注意，使用非递归的方式往往要比使用递归的方式效率更高，比如eg1中求斐波那契数列时候。。。

五、总结

本文首先简单介绍了什么是递归说明了递归的前提条件，之后重点举例来说明递归的使用方法，这里需要注意递归虽好，但不可什么都用递归，要注意代码可读性，效率等多种性能的考量来综合选择非递归与递归的方式~
好了，今天的递归函数就介绍到这里吧~