一、查找

在一组数据中找某一个特定项的算法过程
通常用来判断某个特定项是否在一组数据中，最终返回True或False
常用的查找算法：顺序查找、二分查找、树表查找、哈希查找等

二、二分查找

二分查找又称为折半查找，要求待查表为有序表
将表中间位置记录的关键字与查找关键字比较，如果相等则比较成功；否则利用中间位置的记录缩小区间，继续查找缩小后的区间。
重复上面的步骤直到查找成功，或者子表不存在，则查找失败

三、画图演示

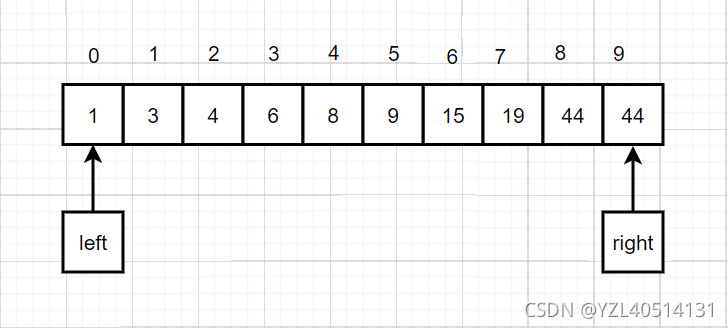
例如查找6是否在数组中
1、找到中间值mid=len(nums)//2==5
2、索引为5时，值为9；比较nums[5]>6，可知目标值在nums[5]的左边
3、将右游标移动，移动到mid-1的位置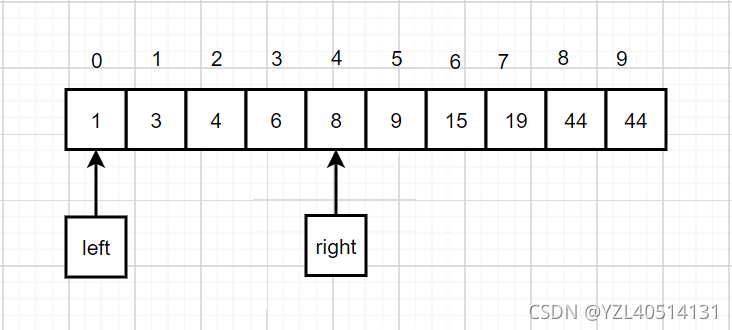

4、找到中间值mid=len(nums)//2=2
5、索引为2时，值为4；比较nums[2]<6，可知目标值在nums[2]的右边
6、移动左游标，移动到mid+1的位置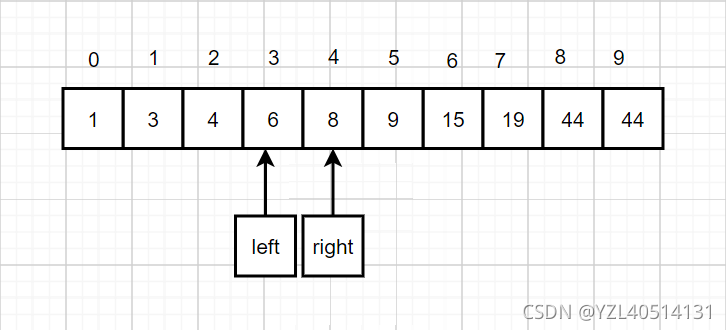

7、找到中间值mid=len(nums)//2=1
8、索引为1时，值为8；比较nums[1]>6，可知目标值在nums[2]的左边
9、将右游标移动，移动到mid-1的位置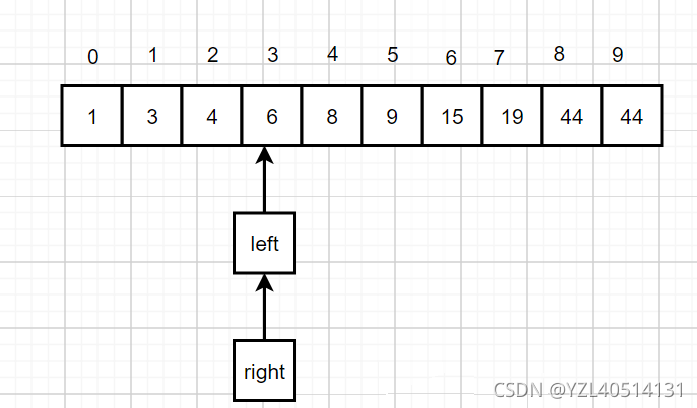

10、此时左游标和右游标重合
11、找到中间值mid=len(nums)//2=0
12、索引为0时，值为6；比较nums[1]=6，找到目标值，否则数组中没有目标值

四、代码块

采用递归方法
时间复杂度为O(logn)

def binary_search(nums,target,left,right):
    '''
    二分查找递归版
    :param nums: 待查找的数组，要求时升序的
    :param target:要找的的数字
    :param left:区间的左边索引
    :param right:区间的右边索引
    :return:target在nums中就返回True，否则返回False
    '''
    #递归的结束条件，left>right
    if left>right:
        return False
    #找中间值
    mid=(left+right)//2  #中间值的索引
    #判断中间值是否等于目标值
    if nums[mid]==target:
        return True
    #如果中间值小于目标值，说明目标值只能在中间值的右边区间
    if nums[mid]<target:
        left=mid+1
        return binary_search(nums,target,mid+1,right)
    # 如果中间值大于目标值，说明目标值只能在中间值的左边区间
    return binary_search(nums,target,left,mid-1)


test=[1,3,4,6,8,9,15,19,44,44]
print(binary_search(test,15,0,len(test)-1))
print(binary_search(test,14,0,len(test)-1))